一、数据集
| 序号 | X1 | x2 | x3 | x4 | Y | 序号 | X1 | x2 | x3 | X4 | Y |
| 1 | 26 | 6 | 60 | 78.5 | 7 | 8 | 31 | 22 | 44 | 72.5 | 1 |
| 2 | 29 | 15 | 52 | 74.3 | 1 | 9 | 54 | 18 | 22 | 93.1 | 2 |
| 3 | 56 | 8 | 50 | 104.3 | 11 | 10 | 47 | 4 | 26 | 115.9 | 21 |
| 4 | 31 | 8 | 47 | 87.6 | 11 | 11 | 40 | 23 | 34 | 83.8 | 1 |
| 5 | 52 | 6 | 33 | 95.9 | 7 | 12 | 66 | 9 | 12 | 113.3 | 11 |
| 6 | 55 | 9 | 22 | 109.2 | 11 | 13 | 68 | 8 | 12 | 109.4 | 10 |
| 7 | 71 | 17 | 6 | 102.7 | 3 |
1、从中选取主要变量，建立与因变量y的回归方程；
2、考察因变量x1,x2,x3,x4是否存在多重共线性。
二、建立y与x1,x2,x3,x4的多元回归方程
x1<-c(26,29,56,31,52,55,71,31,54,47,40,66,68)
x2<-c(6,15,8,8,6,9,17,22,18,4,23,9,8)
x3<-c(60,52,50,47,33,22,6,44,22,26,34,12,12)
x4<-c(78.5,74.3,104.3,87.6,95.9,109.2,102.7,72.5,93.1,115.9,83.8,113.3,109.4)
y<-c(7,1,11,11,7,11,3,1,2,21,1,11,10)
df<-data.frame(y,x1,x2,x3,x4)
lm.reg<-lm(y~x1+x2+x3+x4,data=df)
summary(lm.reg)
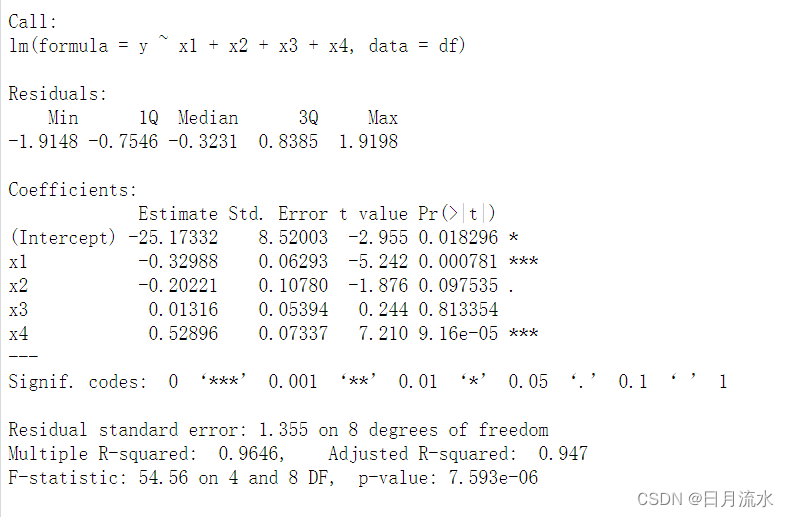从回归方程的结果可以看到，从回归方程系数的t检验的p值得出，只有变量x1,x4系数显著，x2和x3系数不显著。
三、共线性诊断，考察变量之间的共线性关系
共线性是指在进行多元线性回归时，自变量至简存在线性关系或近似线性关系，自变量的线下关系将会导致参数估计的误差增大，会产生不稳定的模型。通过计算回归方程的方差膨胀因子来测度模型的多重共线性问题。
基本介绍来自百度搜索
一般的标准是当方差膨胀因子VIF>10，表明模型存在较强的多重共线性。
下面使用R语言中的DAAG程序包中的vif()函数计算方程膨胀因子
library(DAAG)
vif(lm.reg,digits=5)
运行得到：
所有自变量的方差膨胀因子均小于10，无明显的共线性关系，但x1和x4的VIF值较大，
可以计算出x1和x4的相关系数为
cor(x1,x4) [1] 0.816252 有较强的相关性。
四、使用R语言中的逐步回归函数找到最优的回归方程。
lm.step<-step(lm.reg)
summary(lm.step)
运行得到：
。
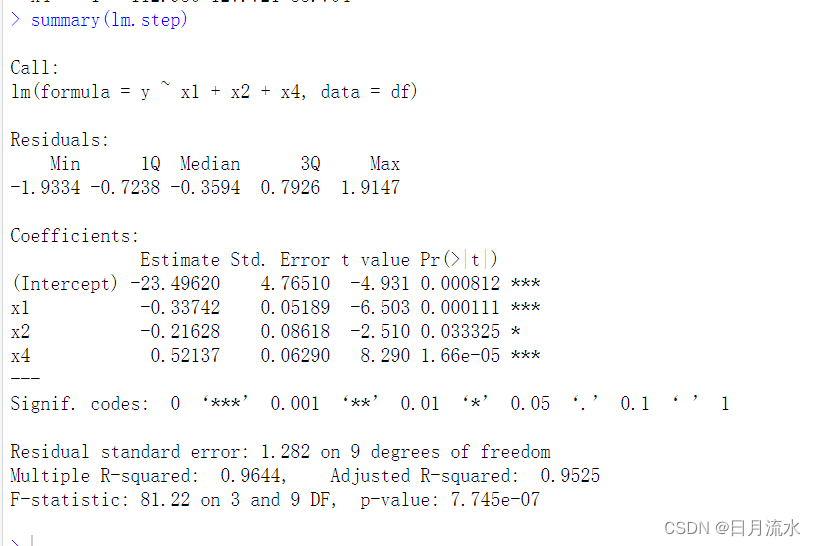使用step()函数得到最后的回归方程：
y=-23.49620-0.33742*x1--0.21628x2-0.52137x4
函数根据AIC信息量最小原则，最终过掉了变量x3,保留了自变量x1,x2,x4.
从检验结果中可以看到，回归方程和回归方程的系数显著，通过了F检验和t检验。
