【算法小讲堂】#1 贪心算法

引入——关于贪心算法

我们先来做一个小游戏——现在假设自己是一个小偷，桌上有一些物品，包括一台iPhone15、一个充电宝、一个眼罩和一个溜溜梅。此时，你听说警察即将到来，那么你会先带走哪个东西呢？

一般来讲，时间一定的话，我们通常会先拿走桌面上最贵的物品。

“先拿最贵的走”，这种思想就是贪心。

贪心算法解决的问题大致如此——

【从大集合中选出东西】

排序
按顺序选

如此，收益最大。

可是，为什么每次选“最贵的”，最终收益就是最大的？

这并不明显。

很多时候，贪心算法需要严格方式证明，在不同的情景下。

示例——排队接水问题

$n$ 个同学排队接水，接水的时间分别是 $t 1$ ， $t 2$ ， $t 3$ ， $t 4$ ， $t 5$ ，…， $t n$ 。

如何安排同学接水的顺序？
使得平均接水时间最短。
并计算出最短的平均接水时间。

分析——特例假想

假设这 $n$ 名同学打水的时间普遍较短，除了其中的同学小明，他拿了一个水塘大（夸张）的盆来打水。

此刻，如果让他站在队伍的最前面，其他同学等待时间是不是就非常非常久了，我们的平均等待时间想必就非常大了。

因此，合理的安排是——

让打水快的同学尽可能站在队伍前面。

模型——解决问题的一般方法

我们需要按一定的步骤解决此类问题，一般来讲，第一步是排序，明白什么样的同学应该排在前面；第二步是选择，模拟此过程计算出平均接水时间。

A 排序

找到符合贪心思想的排序方案——打水快的排前面。

B 选择

依次序进行选择，模拟目标过程计算所需答案。

补充数学证明

这种符合直觉的贪心方法未必能够经得起数学的推敲。为了保证做法的正确，我们通常还要建立数学模型，利用数学手段证明这一解决问题的方法是行之有效的。

在贪心算法的问题中，常见地需要使用到诸如排序不等式的数学公式。

一些尝试——加上一些限制条件

在一开始，我们假设了一个情境。

此时我们希望加入再一些限制条件，使得其更符合现实生活——

背包的容量是有限的
每一样物品是既有重量又有价值的

倘若这样，那么我们就不仅仅需要考虑物品的价值。

因为向背包装入最贵的东西后，可能再也没用地方装下其余同样有很高价值但重量小的物品了。

请添加图片描述

此类问题成为了相对复杂一些的01背包问题。

现实生活中，还可能有以下情形——

由于警察并不一定往往在最后赶到，实际应该是在不同时刻赶到的概率是不相同的。

此时，我们需要利用动态规划解决，以求得最大的数学期望。

再看冒泡排序——排序的贪心本质

请添加图片描述

先假定一个情形——你拿到一堆标着数字的卡片（可能有100张），你需要做的是给卡片按数字从小到大的顺序进行排序。

你本能会做的是先铺开这些卡片，整体上看看这些数字大小。

当你的眼睛落在任意两张不同数字的卡片上，会有这样的情况——

（左边的卡片是 $N 1$ ，右边的卡片是 $N 2$ ）

目标的情形是 $N 1 < N 2$ ，所以如果左边的数字大于右边的数字，我们尝试交换。

显然，这种做法没有什么条理。但是可以确信的是——

在每一次操作后，我们都更加接近那个正确的答案。

而经过有限次操作后，就一定能够得到最优解，即正确的排序。

而冒泡排序，其实就是按照一定的规律执行判断-交换的步骤。

思想的本质依旧是贪心。

贪心的局部探索——动态规划

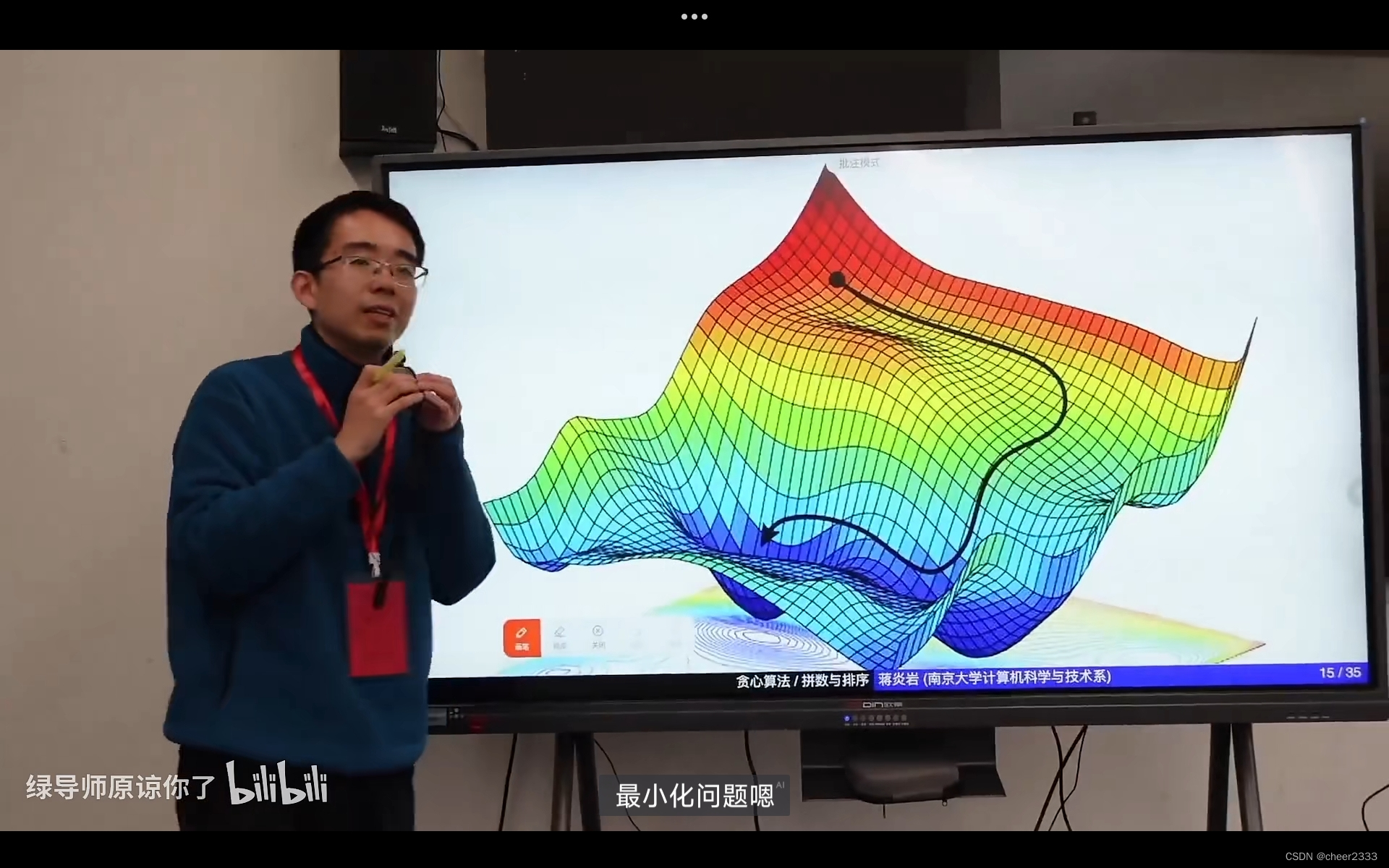
请添加图片描述

一个思考问题：给出一个山的三维模型（图片见上），目标求得此山中的最低点。

假设你是一位在这个山中迷路的攀登者，而山里起了大雾，你需要尽快到山的低洼处修整。你只能知道你所站的地方的坡度，没有其余办法找到那个低洼处。

此时，为找到低洼处，我们会做的一定是一直向**“下”走，即一直下坡，直到不能再下坡**。

最终找到的未必是最低点，寻找的过程中很有可能一步就走到了再也回不去的道路（指远离最优解），但是我们知道，至少这样，让我们错误的概率更小一些。因为哪怕这个点不是全局中的最优解，它也会是我在这个区域能够找到的最好的解。

这个试探的过程，我们称之为局部搜索。

贪心算法的问题实例

🟢 [NOIP1998 提高组] 拼数

比较传统的贪心问题，解决问题的关键在于比较和交换相邻的数字串，一步步逼近最佳的答案。

题目描述

设有 $n$ 个正整数 $a_1 \dots a_n$ ，将它们联接成一排，相邻数字首尾相接，组成一个最大的整数。

输入格式

第一行有一个整数，表示数字个数 $n$ 。

第二行有 $n$ 个整数，表示给出的 $n$ 个整数 $a_i$ 。

输出格式

一个正整数，表示最大的整数

样例 #1

样例输入 #1

3
13 312 343

样例输出 #1

34331213

样例 #2

样例输入 #2

4
7 13 4 246

样例输出 #2

提示

对于全部的测试点，保证 $\leq n \leq 20$ ， $\leq a_i \leq 10^9$ 。

NOIP1998 提高组第二题

🟢 [NOIP2012 提高组] 国王游戏

此题级别为普及+/提高。

与前面一题不同的是，这里增加了变量，考虑时不妨先手动从简单的情形起开始模拟。

题目描述

恰逢 H 国国庆，国王邀请 $n$ 位大臣来玩一个有奖游戏。首先，他让每个大臣在左、右手上面分别写下一个整数，国王自己也在左、右手上各写一个整数。然后，让这 $n$ 位大臣排成一排，国王站在队伍的最前面。排好队后，所有的大臣都会获得国王奖赏的若干金币，每位大臣获得的金币数分别是：排在该大臣前面的所有人的左手上的数的乘积除以他自己右手上的数，然后向下取整得到的结果。

国王不希望某一个大臣获得特别多的奖赏，所以他想请你帮他重新安排一下队伍的顺序，使得获得奖赏最多的大臣，所获奖赏尽可能的少。注意，国王的位置始终在队伍的最前面。