基于相位的运动放大:如何检测和放大难以察觉的运动
目录
- 一、说明
- 二、结果的峰值
- 三、金字塔背景
- 3.1 可操纵金字塔
- 3.2 亚倍频程复数可控金字塔
- 四、基本方针
- 4.1 1D 问题陈述
- 4.2 一维方法
- 4.3 实际实施说明
- 五、放大倍率的限制
- 5.1 空间支持的影响
- 5.2 频带的影响
- 六、推导放大范围
- 6.1 将频率纳入运动界
- 6.2 降低八度以增加放大倍率
- 七 处理噪音
- 7.1 原理
- 7.2 滤波相位增量
- 八、总结
- 九、结论
一、说明
当我第一次接触到运动放大时,我很惊讶,移动不到一个像素的东西怎么会有运动放大?没错,我们实际上可以检测和放大静态视频中难以察觉的运动,而且我们可以在不放大噪音的情况下做到这一点!这个概念有很多应用,并且已经在多个行业中使用。例如,结构和设备并不总是容易安装传感器。可靠的视觉技术可以成为快速识别和诊断问题的有效方法,这提供了低成本的结构分析。
第 1 部分:背景和理论(本)
第 2 部分:Python 实现
二、结果的峰值
下面的 GIF 显示了基于相位的运动放大的几个示例,原始视频在左侧,运动放大视频在右侧。在每个 GIF 中,处理仅应用于 YIQ 色彩空间中的亮度通道。

图 1. 放大系数为 25 的运动放大起重机视频。

图2.运动放大吉他弦,放大倍数为 25。
这不是最新的AI,原始论文是2013年的。在这篇文章中,我们将解开论文中的主要概念,并了解基于相位的运动放大背后的细节。在第 2 部分中,我们将在 Python 中从头开始实现它,并学习如何制作如上所示的视频和 GIF。
三、金字塔背景
大部分背景知识涉及理解复杂可操纵金字塔,以及可选的亚倍频程复杂可操纵金字塔。为简洁起见,我们仅在此处进行总结,详情请参阅链接的帖子。
3.1 可操纵金字塔
可操纵金字塔是一种线性的多尺度和多方向图像分解,使我们能够在不同的频带和方向上观察图像。每个滤波器都占据频域的连续区域,并具有定位在空间域中的脉冲响应。在实践中,我们生成了一组不同频段和方向的频域滤波器以及非定向高通和低通分量,然后在频率空间中进行分解。该转换没有混叠,并且过度完成,这意味着它包含足够的信息来重建原始图像。
复杂可操纵金字塔在多个尺度和方向上添加了局部相位的概念。一般来说,相位告诉我们事物在图像中的位置,而局部相位只是某个位置的相位概念,例如图像左下角的相位。如果我们看到视频序列中的相位变化,这意味着图像中的事物正在移动。视频序列中的局部相位描述了图像在给定位置的变化方式,这正是我们将用来放大运动的内容。关键是要知道如何使用它,我们将在本文后面介绍。
复杂可控金字塔提供局部相位信息,用于描述视频帧在给定位置的变化方式
3.2 亚倍频程复数可控金字塔
默认情况下,可操纵金字塔的频率滤波器相距一个倍频程。由于频域支持与空间域支持成反比,因此我们可以通过在频域中缩小滤波器来增加滤波器的空间域支持。这就是Sub-Octave滤波器的全部功能。例如,如果我们有半倍频程滤波器,那么需要两个倍频程滤波器才能代替单个倍频程滤波器。我们稍后将看到,亚倍频程滤波器对于大型运动放大至关重要。
在这篇文章中,我们将大量讨论复杂可操纵金字塔,从现在开始,我们将以简写的方式将它们称为金字塔。
四、基本方针
在我们全力以赴尝试用视频来做到这一点之前,让我们先考虑一下 1D 中的事情。通过这篇文章,概念将在 1D 中解释,并附有将其与 2D 实用方法相关的注释。
4.1 1D 问题陈述
考虑一个空间信号 f(x),它可以通过某个瞬态位移函数 δ(t) 进行位移,位移的信号为:f(x + δ(t)))。我们希望将位移放大 α 倍,使放大的位移信号为:f(x + (1 + α)δ(t)))。
4.2 一维方法
我们可以使用傅里叶级数分解来表示复正弦曲线的信号。这种分解为复正弦曲线是我们用于视频的金字塔分解的 1D 模拟。傅里叶分解。修改自源代码。
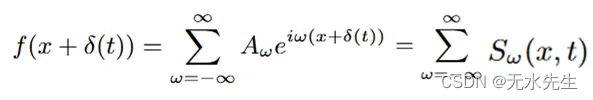
每个正弦波的相位 ω(x + δ t)) = ωx + ωδ(t) 包含运动信息,其中 ω 对应于单个频带。我们需要做的第一件事是隔离与运动相关的相位信息。直流分量:ωx 表示底层空间信号,对应于静态背景。如果我们去掉它,我们就剩下 ωδ(t) 分量,其中包含我们希望放大的运动信息。我们将其表示为带通阶段 B。
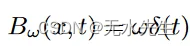
然后,我们可以按α比例缩放 B,并在频域中获得放大的运动,以获得运动放大的复正弦曲线。
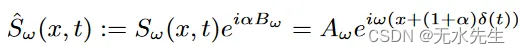
我们对每个子带ω都这样做,以获得空间域中的全运动放大信号:f(x + (1 + α)δ(t)))。
4.3 实际实施说明
在实践中,我们可以使用参考系的局部相位来估计直流分量ωx的值,以便我们可以提取运动信息。我们从电流帧处的相位中减去参考相位,得到运动信号ωδ(t)。由于我们假设视频大部分是静态的,因此这种方法往往效果很好。
除了去除直流分量外,我们还对相位增量进行时间带通滤波,以隔离某个感兴趣的时间频带。这对如何使用运动放大有很大的影响,因为我们能够可视化我们选择的任何频段。例如,我们可以可视化已知的感兴趣频率,也可以扫描多个频段以发现隐藏的运动。
在视频帧中,运动是局部的,这意味着帧中一个位置的对象相对于其他位置的其他对象以不同的方式移动。因此,δ(t) 实际上是 δ(x, t),其中空间变量 x 允许我们根据空间位置区分时间 t 的运动。
五、放大倍率的限制
事实证明,我们可以放大运动的程度是有限的。除了看起来很荒谬之外,极大的运动放大倍率并不能代表真实的信号。换句话说,错误的特征将被放大!此限制来自金字塔筛选器的两个方面:
- 滤波器的空间支持→空间覆盖
- 滤波器的空间频带→中心频率
让我们看两个一维示例,以了解为什么它们会限制放大倍率。
5.1 空间支持的影响
金字塔滤波器的空间支持有一些滚降,我们可以使用高斯窗口在一维中近似它。在此示例中,考虑一个由复正弦曲线和高斯窗口组成的函数 f。
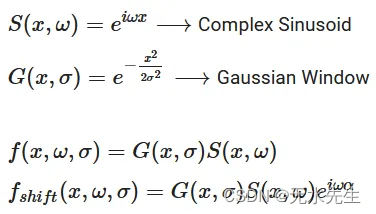
f 的参数是:频率 ω、位置向量 x 和标准差 σ。我们可以将这个函数移动一个倍α正如我们之前所看到的,这个相移对应于运动放大倍率。由于窗口化,我们只能在高斯窗口的范围内移动它。让我们在 Python 中实现它以更好地理解它,用于此的笔记位于 GitHub 上。
S = lambda x, omega : np.exp(1j*omega*x)
G = lambda x, sigma : np.exp((-x**2)/(2*sigma**2))x = np.arange(-15, 15, 0.01)
octaves = 1 # number of octaves for Gaussian window
sigma = octaves*np.pi # std dev of Gaussian window
omega = np.pi/4 # frequency
alpha = np.pi/2 # initial phase shift factorsignal = S(x, omega) * G(x, sigma)
shifted = S(x, omega) * G(x, sigma) * np.exp(1j*omega*alpha)
下面的 GIF 显示了复正弦波的实部和虚部的相移。
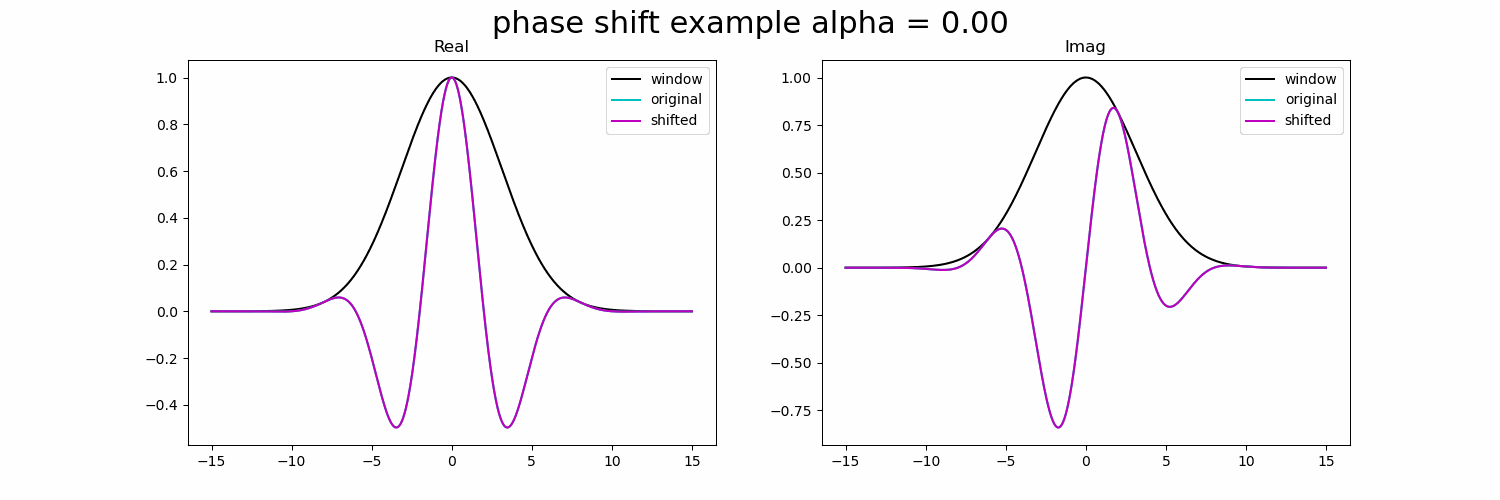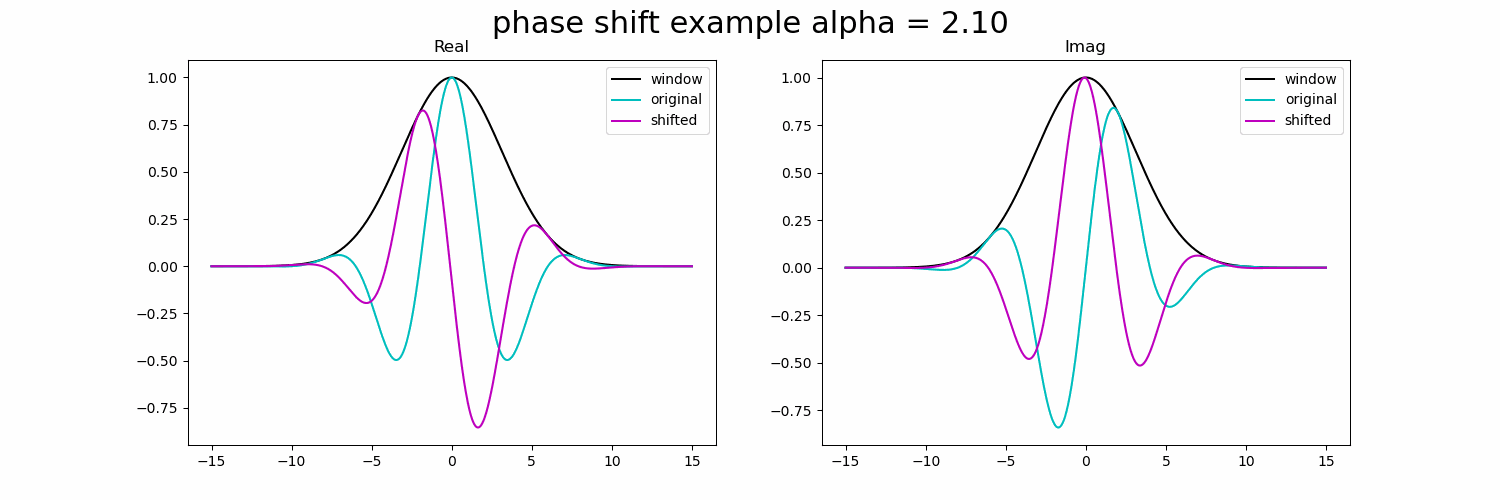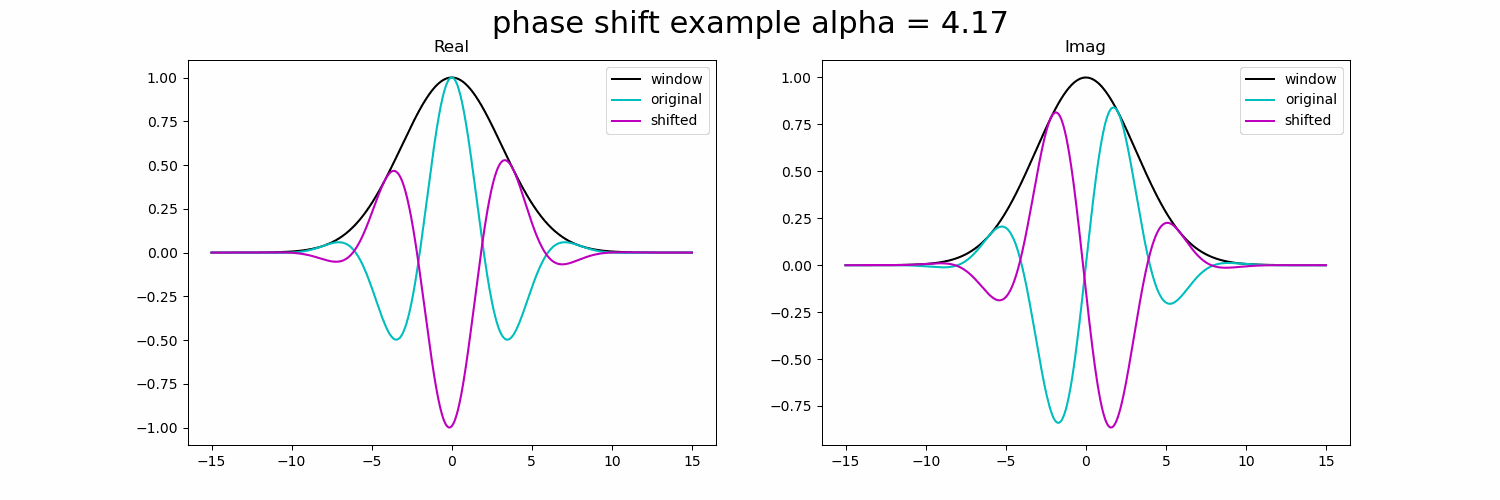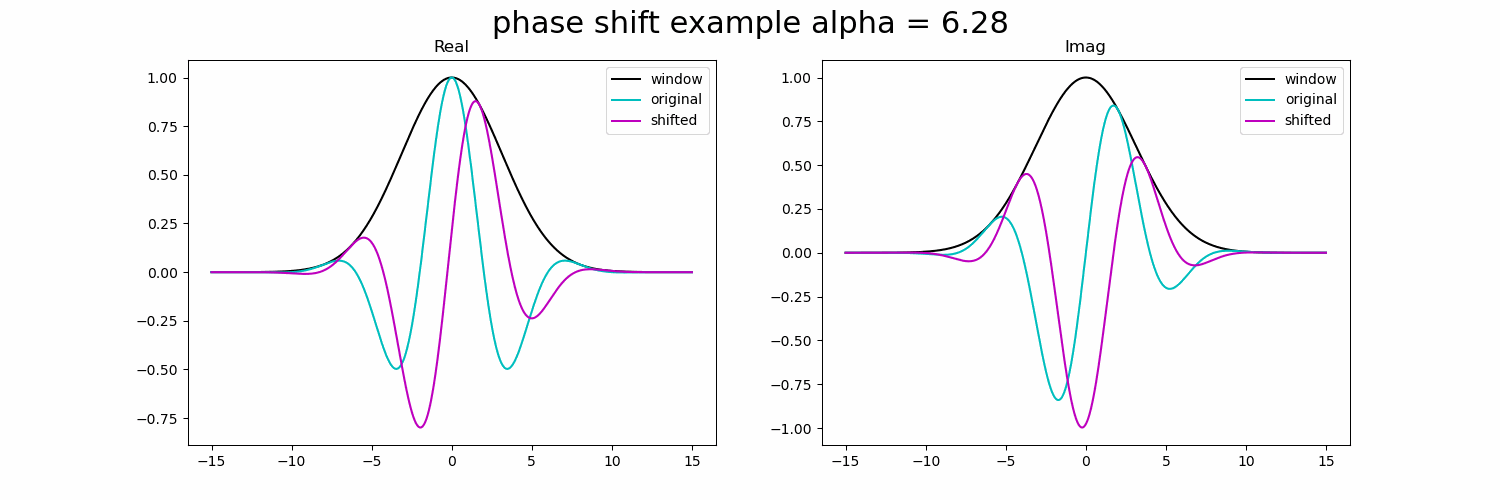
图3.具有复正弦波的相移示例。
一旦我们将相位偏移一定量,振幅将由于高斯窗口而高度衰减。如果我们可以增加高斯窗口的大小(增加它的空间支持),那么我们可以扩展这个限制并实现更大的偏移,而不会有那么多的衰减。
回到 2D 中,这意味着我们只能将运动放大一定数量的像素,然后才能将信号降级到无法识别的程度。此限制基于金字塔过滤器的空间支持。如果我们要增加空间支持,那么我们可以执行更强烈的放大倍率,并且仍然准确地接近真实的移位信号。
5.2 频带的影响
当我们应用运动放大倍率时,我们将其应用于单个金字塔滤镜。我们可以应用的有用运动放大倍率与滤波器的频带直接相关。让我们通过比较两种不同频率下的相移效应来在一维中说明这一点。(从现在开始,我们将只看正弦曲线的实部)。
omega1 = 0.2 # frequency 1
omega2 = 1.0 # frequency 2signal_1 = S(x, omega1) * G(x, sigma)
signal_2 = S(x, omega2) * G(x, sigma) alpha_vals = np.arange(0, 2*np.pi, 0.025)for i, alpha_val in enumerate(alpha_vals):f_shifted_1 = signal_1 * np.exp(1j*omega1*alpha_val)f_shifted_2 = signal_2 * np.exp(1j*omega2*alpha_val)
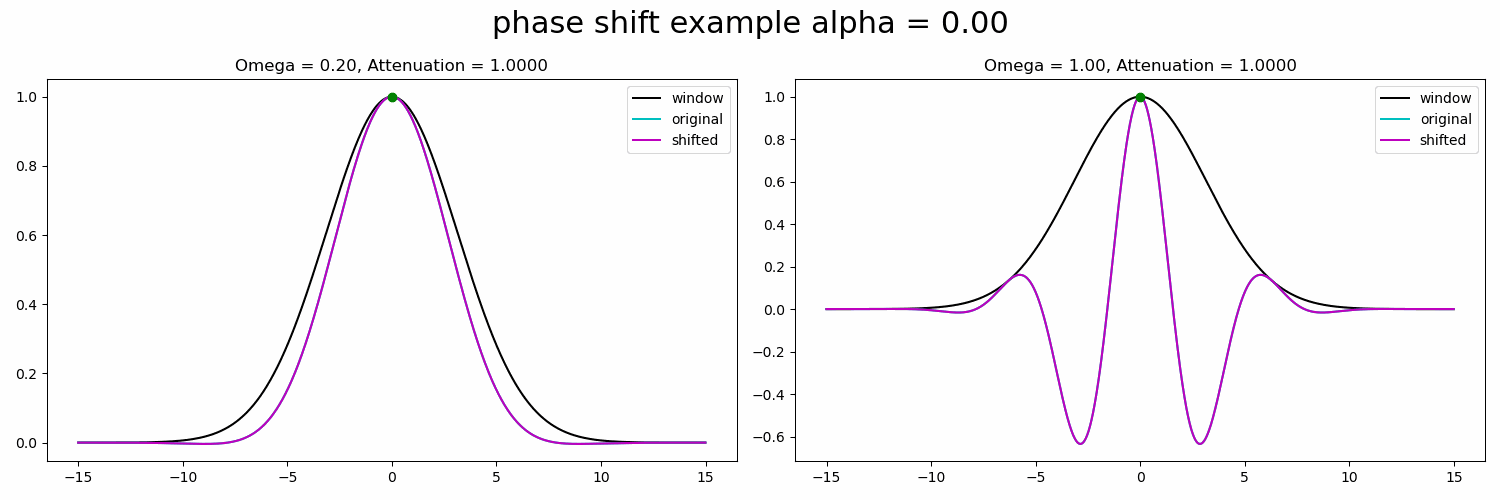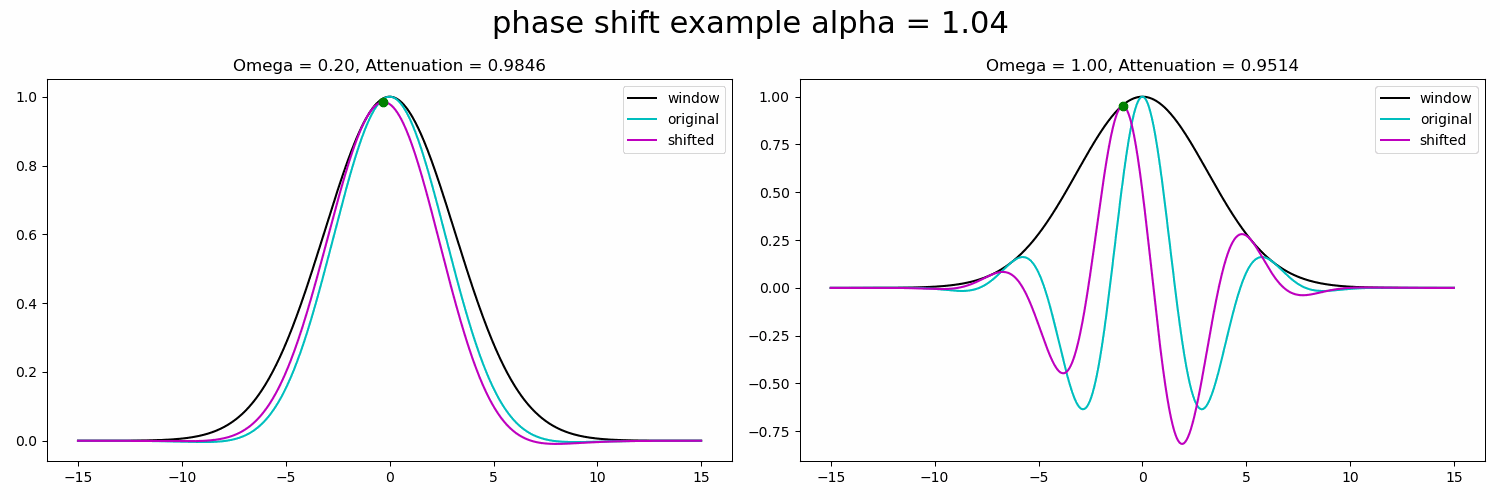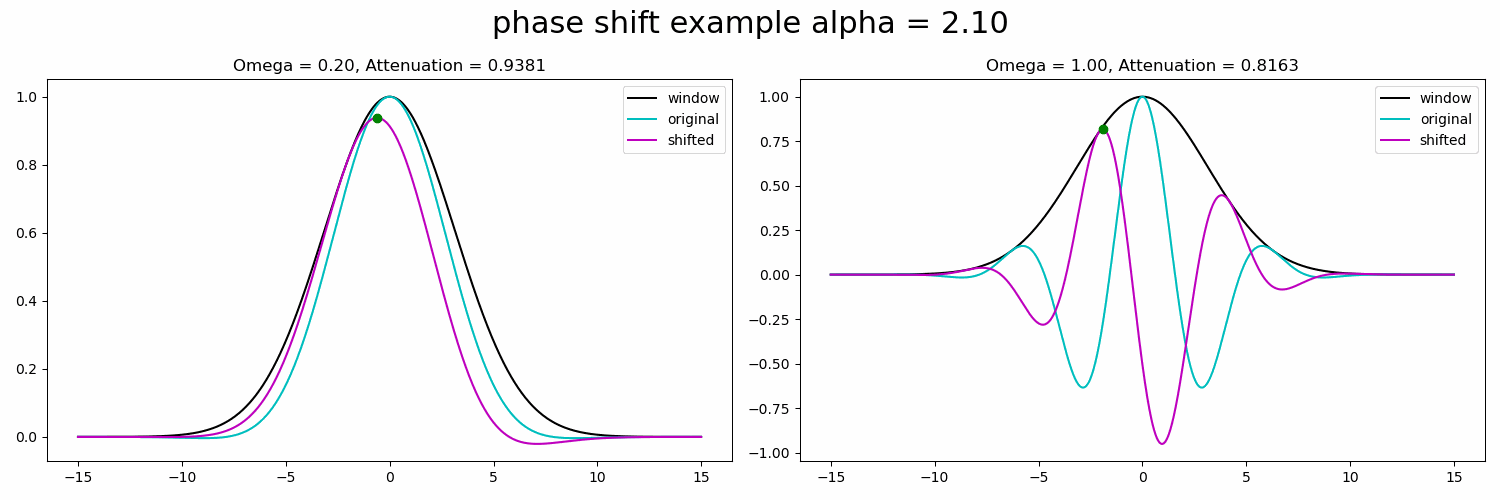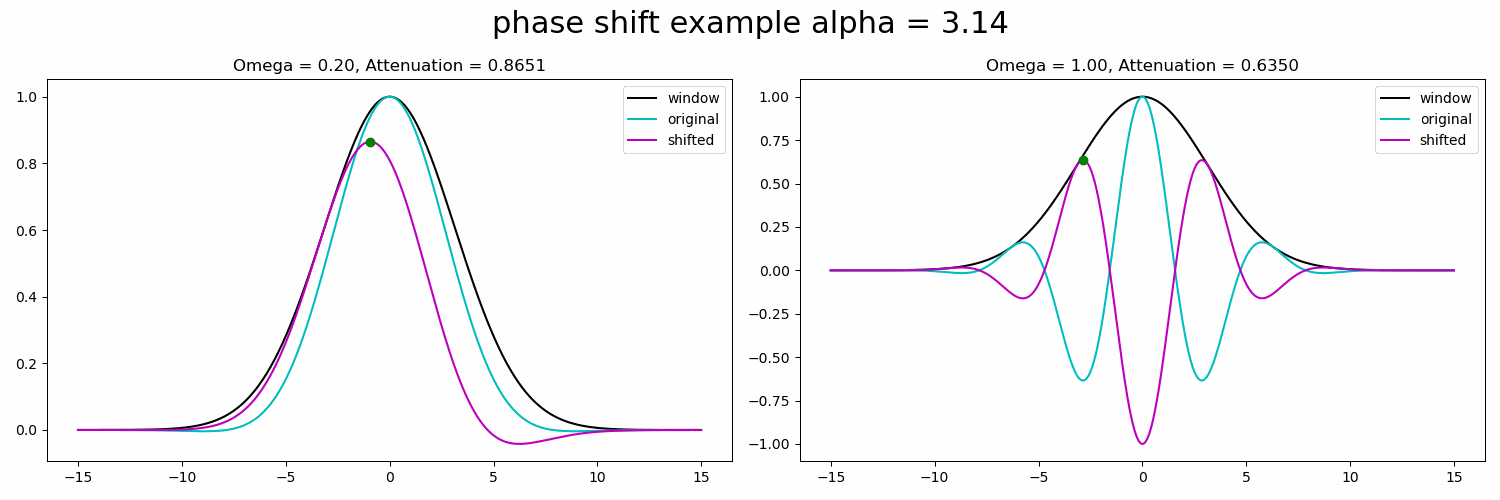
图4.相移对全倍频程高斯窗口内不同频段的影响。仅显示复正弦曲线的实部。资料来源:作者。
两个正弦波的偏移量相同,但请注意频率较高的右侧衰减量较大。更糟糕的是,如果我们继续前进,我们将得到一个翻转(由于周期性),所以主导特征甚至不会是我们打算放大的特征。
大放大倍率在较高的空间频率下具有更大的衰减
六、推导放大范围
您可能会问自己,在降低信号质量之前,我们可以将运动放大多少?我很高兴你问,我们实际上可以根据高斯窗口近似推导出放大倍率的理论界限。我们简单地将运动绑定为高斯窗口的一个标准差,因此我们至少保持原始信号的 ~61%。
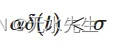
好吧,这似乎不是很有见地,我们所做的只是根据标准差进行任意的截止。边界的真正用途是观察某些因素(如频率和倍频程带宽)如何影响运动放大倍率和信号衰减关系。
6.1 将频率纳入运动界
在全倍频程带宽滤波器(复数可控金字塔提供)中,我们在窗口下大约有一个周期的正弦曲线。如果我们假设窗口的全宽约为 4σ,那么我们得到:

其中ω对应于滤波器的频带。这提供了频率 ω 或波长 λ 的界限:
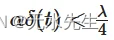
该界限总结了信号频率与有用放大倍率之间的关系,即没有极端衰减的放大倍率。它告诉我们,较低频率(较长)的放大信号比较高频率的信号经历的衰减更少。现在让我们看看倍频程带宽如何影响放大倍率范围。
6.2 降低八度以增加放大倍率
如前所述,增加滤波器的空间支持将使我们能够在减少信号衰减的情况下增加放大倍率。亚倍频程意味着我们正在减少滤波器的频率支持(使它们在频率空间中更小),这反过来又增加了每个滤波器的空间支持。例如,半倍频程意味着两个半倍频程滤波器在频率空间中取代了单个全倍频程滤波器。在一维中,半倍频程高斯窗口可以支持正弦曲线的两个周期,我们可以相应地修改我们的边界。

更进一步,四分之一倍频程带宽高斯窗口可以支持正弦波的四个周期。我们可以用倍频程带宽来概括边界,其中放大倍率的边界变大,倍频程带宽减小。
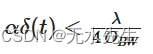
这是一张 GIF,显示了 Sub-Octave 的影响。
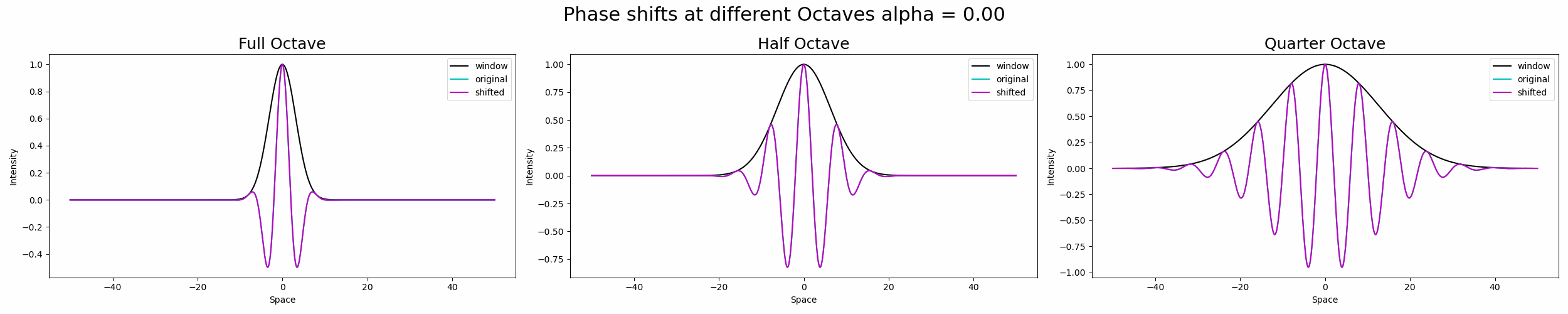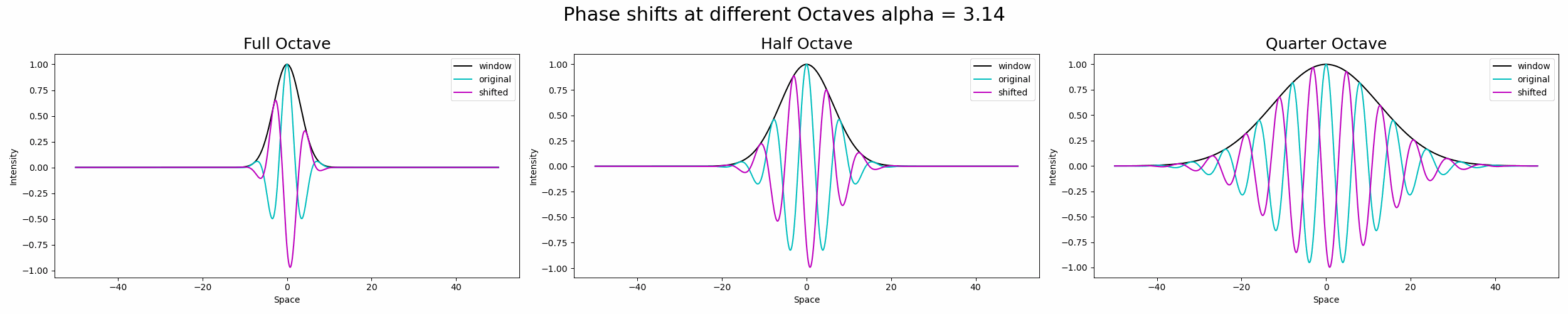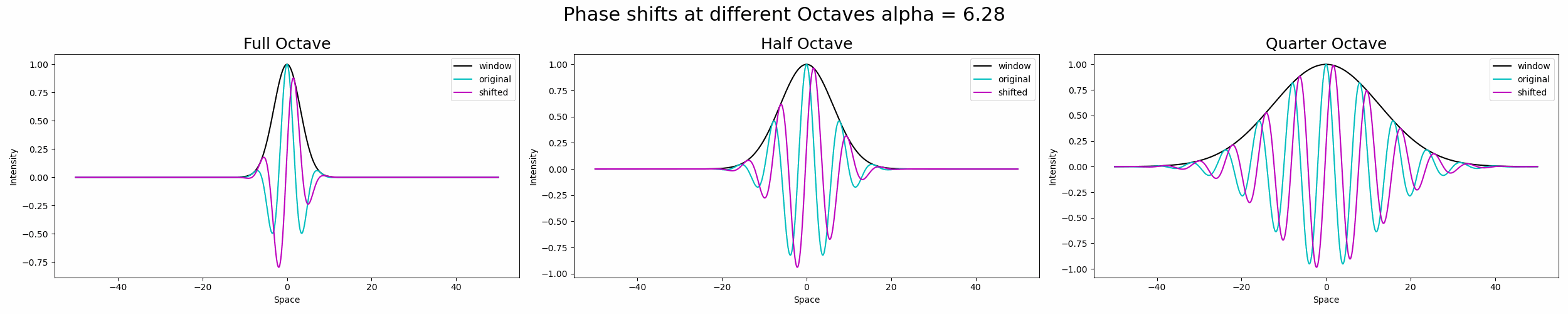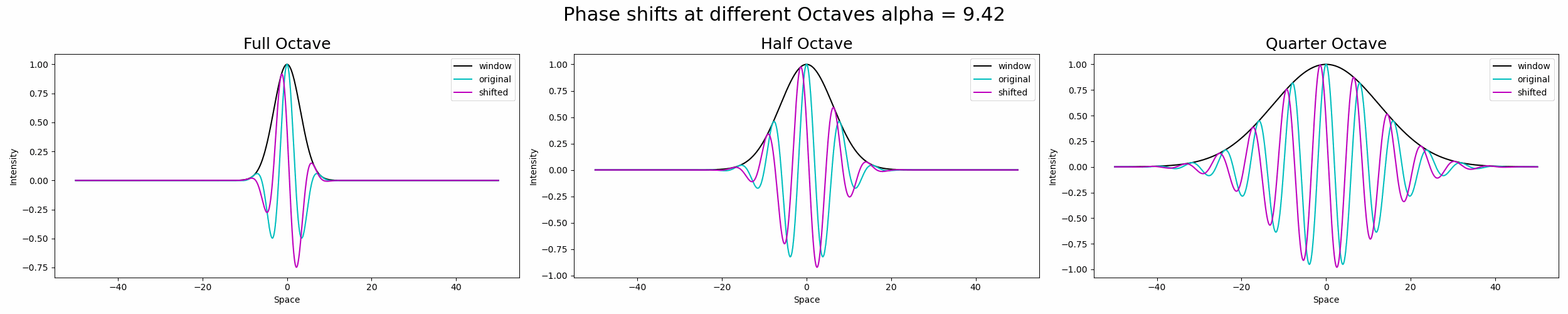
图5.正弦波在不同倍频程带宽的高斯窗口下移位。资料来源:作者。
我们还可以使用由高斯窗口化的局部函数来可视化移位。

图6.局部函数在不同倍频程带宽的高斯窗口下发生偏移。资料来源:作者。
上面的 GIF 显示,在四分之一倍频程窗口下的移位信号达到 0.60 之前,全倍频程高斯窗口中的移位信号被长期衰减为 0。
七 处理噪音
7.1 原理
这种基于相位的运动放大方法实际上并没有放大噪声,而是通过移动的运动将其转换。考虑一个带有附加噪声的图像 I:I + σnn,其中噪声功率 σn 远小于图像信号 I。它在频率 ω 的金字塔滤波器下的响应表示为:

其中 N 是噪声对滤波器的响应 由于我们假设噪声远小于信号,因此我们也假设对应于运动的相位近似等于 ωδ(t),就像我们之前看到的一样。放大的运动响应为:
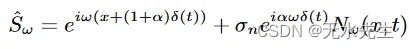
运动放大滤波器响应中的噪声项现在具有相移 αωδ(t),对应于噪声的平移,而不是放大。这与这种基于阶段的方法的基础知识有关。我们不是直接放大信号,而是通过对感兴趣的特征进行相移来放大运动。碰巧的是,我们也放大了噪声的运动(将噪声从一个点移动到另一个点),但我们实际上并没有增加噪声功率。
7.2 滤波相位增量
尽管这些假设意味着滤波相位将等于ωδ(t),但我们仍然需要意识到噪声会破坏相位信号并导致不正确的运动被放大。为了解决这个问题,我们可以过滤获得的相位差。为此,我们使用幅度加权滤波器对每一帧的相位差应用空间高斯模糊。

其中 φ 是金字塔滤波器 i 和视频帧 k 处的相位信号,A 是电流滤波器响应的幅度,K 是标准偏差为 ρ 的高斯核。
八、总结
基于相位的运动放大率概述如下所示:

图7.基于相位的运动放大概述。来源。
需要注意的是,我们一次对单个金字塔过滤器执行处理,并且通常对视频的所有帧执行处理。但是,处理不是在高通和低通金字塔组件上执行的,它们保持不变,并在最后一步重新合并。
🇦 → 使用复杂可操纵金字塔分解图像。
🇧 → 从每个帧中移除直流相位分量,以获得运动信号 ωδ(t) 的相位。然后,将视频帧中的运动/相位信号按时间过滤到目标带宽。
🇨 → (可选)执行幅度加权滤波以对相位信号进行降噪。
🇩 → 在每个滤光片上应用运动放大倍数 αωδ(t)。
🇪 → 重新合并高通和低通组件并折叠金字塔并获得运动放大的视频帧
九、结论
我们已经通过一维示例介绍了基于相位的运动放大的基础知识。我们已经描述了 2D 的基本方法以及它取决于空间支持和频段的局限性。我们已经展示了噪声实际上是如何被放大的,它只是被平移,这是这种方法的一个方便的特点。上面显示了该算法的高级概述,第 2 部分展示了如何实际实现它。
引用
[1] Simoncelli, EP, & Freeman, WT (未注明日期).可操纵金字塔:一种用于多尺度导数计算的灵活架构。论文集,图像处理国际会议。https://doi.org/10.1109/icip.1995.537667
[2] 波蒂利亚,哈维尔和西蒙切利,埃罗。(2000). 基于复杂小波系数联合统计的参数化纹理模型.国际计算机视觉杂志。40. 10.1023/A:1026553619983.
[3] Granlund,GH和Knutsson,H.(2011)。计算机视觉的信号处理。斯普林格。
[4] Wadhwa,N.,Rubinstein,M.,Durand,F.和Freeman,WT(2013)。基于相位的视频运动处理。基于相位的视频运动处理。https://people.csail.mit.edu/nwadhwa/phase-video/
[5] https://rxian.github.io/phase-video/




)
)


)




系统源码)
)



(二))
