目录
1.程序功能描述
2.测试软件版本以及运行结果展示
3.核心程序
4.本算法原理
5.完整程序
1.程序功能描述
Prony算法是一种用于信号处理和系统辨识的经典方法,特别适用于线性时不变系统(LTI)的频率响应分析以及模拟复指数信号序列。其基本思想是通过观测到的时间序列数据,估计出系统中包含的多个复指数函数及其对应的系数,从而揭示系统的动态特性。
2.测试软件版本以及运行结果展示
MATLAB2022a版本运行

3.核心程序
............................................................................
for ij = 1:length(SNR)for k = 1:50[ij,k]%%%参数初始化%参数初始化Fs = 100; %采样频率设置为400Delta = 1/Fs;dt = 1/Fs; %加入直流分量%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%原始的模拟信号%原始的模拟信号ts = 1:0.005:length(n)-1;%测试序列X1 = 3*exp(-0.95.*ts).*cos(3*pi.*ts)+...4*exp(-0.2.*ts).*cos(45.6*pi.*ts+0.5)+...5*exp(-0.3.*ts).*cos(60*pi.*ts)+...6*exp(-0.4.*ts).*cos(80*pi.*ts+0.5)+200;%测试序列 X = awgn(X1,SNR(ij),'measured'); %普罗尼计算 Xs = func_Prony(X,dt);err(ij,k)= mean(abs(X(1:end-1)-Xs(2:end)));end
endfigure;
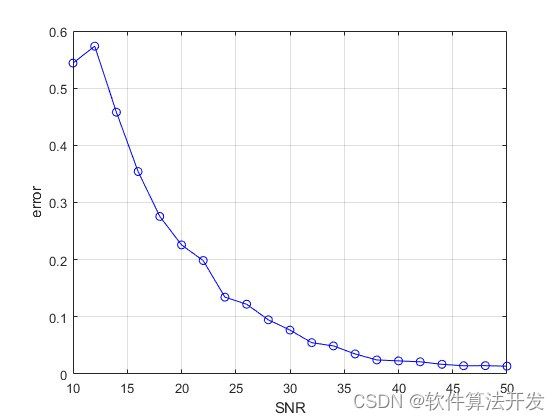
plot(SNR,mean(err,2),'b-o');
grid on
xlabel('SNR');
ylabel('error');
27_006m
4.本算法原理
假设一个LTI系统输出为一个离散时间序列y[n],它是由M个具有不同幅值、角频率和初相位的复指数函数叠加而成:
y[n] = ∑_{m=1}^{M} A_m * exp(j(ω_m*n + φ_m))
其中:
- A_m 是第m个复指数函数的幅值。
- ω_m 是第m个复指数函数的角频率。
- φ_m 是第m个复指数函数的初相位。
- j 是虚数单位。
- n 是时间索引。
Prony算法的目标就是根据观测到的离散序列y[n],求解出Am, ωm, φm这三个参数。
Prony算法的具体步骤:
-
构建过采样矩阵Y: 对于长度为N的数据序列y[n],构造 Hankel 矩阵或Toeplitz矩阵 Y,矩阵元素由 y[n] 的滞后和超前项组成。
-
线性方程组构建与求解: 通过对上一步得到的矩阵进行适当的操作(例如特征分解或最小二乘拟合),可以建立关于幅值A_m、频率ω_m和初相位φ_m的线性方程组,并解这个方程组以获得这些参数的估计值。
-
参数辨识: 解决上述线性方程组后,即可得到系统中各个振荡分量的幅值、频率和初相位,进而实现对系统动态特性的精确辨识。
5.完整程序
VVV







)






)

)
)

