参考资料:用python动手学统计学
1、导入库
# 导入库
# 用于数值计算的库
import numpy as np
import pandas as pd
import scipy as sp
from scipy import stats
# 用于绘图的库
from matplotlib import pyplot as plt
import seaborn as sns
sns.set()
# 用于估计统计模型的库
import statsmodels.formula.api as smf
import statsmodels.api as sm2、数据准备
本次数据为准预测销售额的模型,包含湿度、气温、天气(晴或雨)、价格4个解释变量。天气为分类变量,其余为连续变量。
sales=pd.read_csv(r"文件路径")
sales
3、数据可视化展示
在进行数据分析时,第一步永远是可视化。统计、模型化等工作都要放在后面做。由于及时变量有多个,因此这里绘制散点图矩阵。如下
sns.pairplot(data=sales,hue='weather')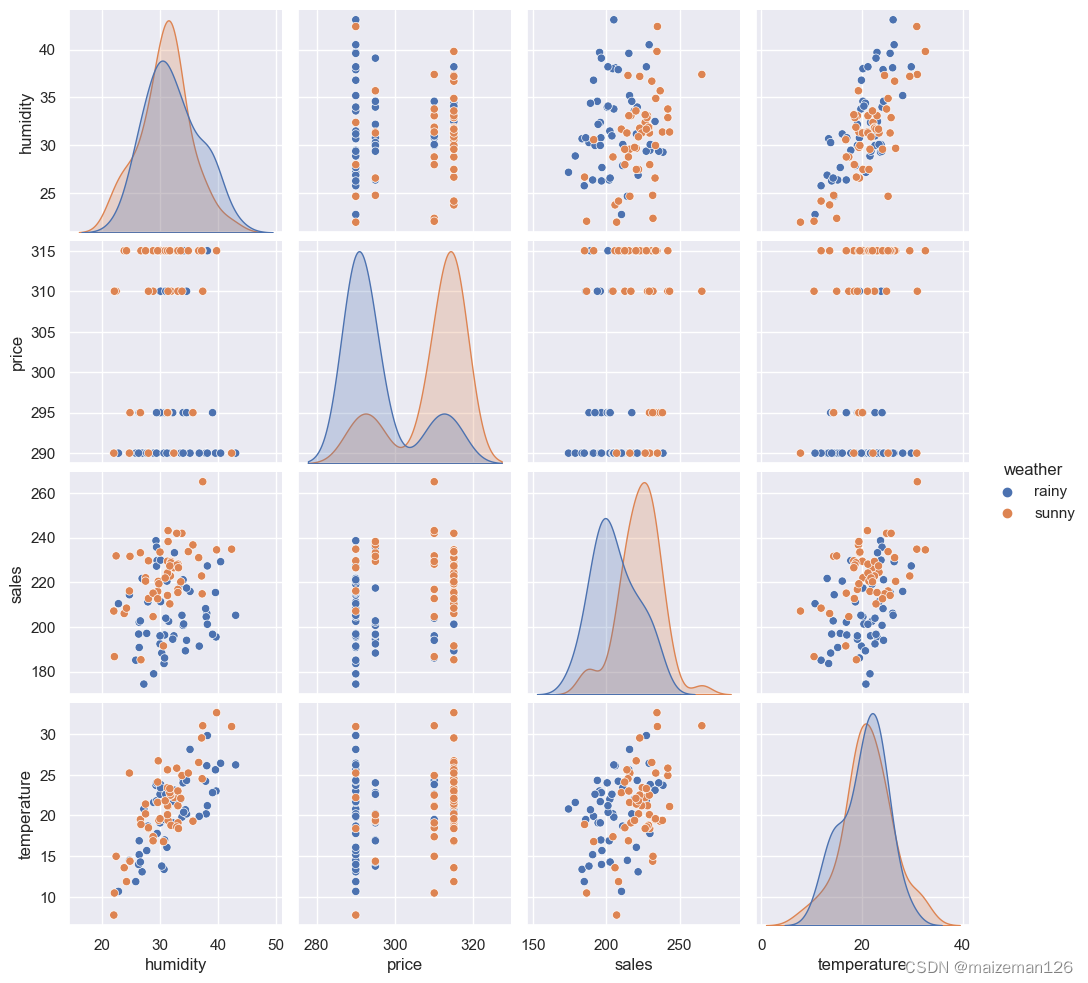
在矩阵图中,可以看出除了气温湿度有明显的正相关关系外,其他因素间没有明显的关系。
4、多解释变量模型
# 拟合多解释变量的模型
# 在定义多解释变量的模型时,解释变量之间用加号连接
lm_sales=smf.ols("sales~weather+humidity+temperature+price",data=sales).fit()
# 输出估计参数
lm_sales.params
5、模型选择
在typeⅠ ANOVA中,如果改变解释变量的顺序,检验结果会不一样。在方差分析中,解释变量的效应是基于残差量化的,变量个数增加时所减少的残差平方和决定了变量的效应。在多解释变量模型中,变量个数增加时所减少的残差平方和决定了变量的效应大小,在这种情况下变量平方和的值会因其添加的顺序不同而不同,对于解释变量是否存在显著性影响的判断也不同。对多解释变量模型进行type Ⅰ ANOVA可能会导致错误的结论。具体示例请查阅:《用python动手学统计学》一书。
type Ⅱ ANOVA是方差分析的一种,它的结果不会因解释变量顺序的不同而不同。typeⅡ ANOVA 根据解释变量减少时所增加的残差平方和量化解释变量的效应。即使解释变量的顺序不同,这种方法的效果也不会改变。通过这种方法得到的组间偏差平方和就叫作调整平方和。
当解释变量只有一个时,type Ⅰ ANOVA与type Ⅱ ANOVA的结果相等。
6、方差分析
# 输出方差分析表
print(sm.stats.anova_lm(lm_sales,typ=2))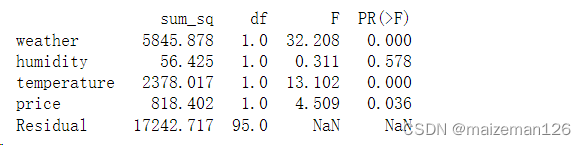
由此方差分析表可知,humidity的p值为0.578,湿度对销售额没有显著影响。
结合前面的可视化作图,可知气温和湿度的相关性很强,因此可能存在这种情况:如果模型中包含了气温,就无法认为湿度会对销售额产生显著影响。下面我们继续对不含湿度的模型进行方差分析。
# 拟合不含湿度的模型
mod_non_humi=smf.ols('sales~weather+temperature+price',data=sales).fit()
#输出方差分析表
print(sm.stats.anova_lm(mod_non_humi,typ=2).round(3))
由上表可知,目前所有变量都是必要的,至此,变量的选择结束。
系数等结果的解读应该使用变量选择后的模型进行,不应该将通过错误的变量组合进行模型化的结果用于预测或解读。
因此,本例的模型参数如下:
mod_non_humi.params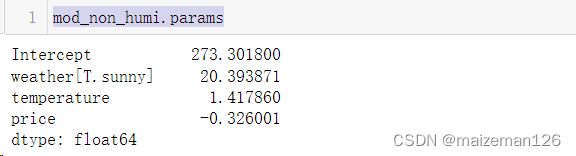
7、使用AIC进行变量选择
如果使用AIC 进行变量选择,就没有必要像方差分析那样更滑计算方法,直接建模并计算AIC即可。
print('包含所有变量的模型:',lm_sales.aic.round(3))
print('不含湿度的模型:',mod_non_humi.aic.round(3))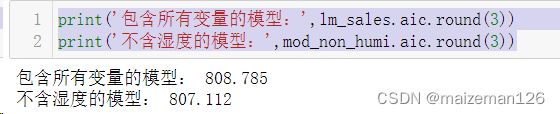
不含湿度的模型的AIC更小,所以湿度不应该包含在销售额预测模型中。原则上应该对比所有变量组合的AIC。
使用AIC进行变量选择的过程是比较固定的。它和系数t检验不同,多水平的变量不会导致多重假设检验问题,所得模型的含义永远是“对未知数据的预测误差最小的变量组合”。AIC也没有检验的非对称性问题。不过,与不能过度信任p值类似,我们也不能过度信任AIC,还应该从系数的含义、变量选择的结果、残差等多个方面综合评估模型。
8、多重共线性
在解释变量之间相关性很强时出现的问题就是多重共线性。在本例中,气温与湿度就是相关的,在解读类似模型时需要注意这一点。
多重共线性问题最简单的解决方案就是去掉强相关变量中的一个。多重共线性会对系数的解读造成干扰,我们应该先进行变量选择再解读结果。
在变量选择的过程中有时会使用检验,但如果变量之间强相关(如相关系数接近1),检验所得的p值也会收到干扰。





)







原理和实现)

)
)


