2.3整数运算
有时候会发现两个正数相加会得出一个负数,而比较表达式x<y和比较表达式x-y<0会产生不同的结果。这些属性是由于计算机运算的有限性造成的。理解计算机运算的细微之处能够帮助程序员编写更可靠的代码。
2 .3. 1 无符号加法
原理:
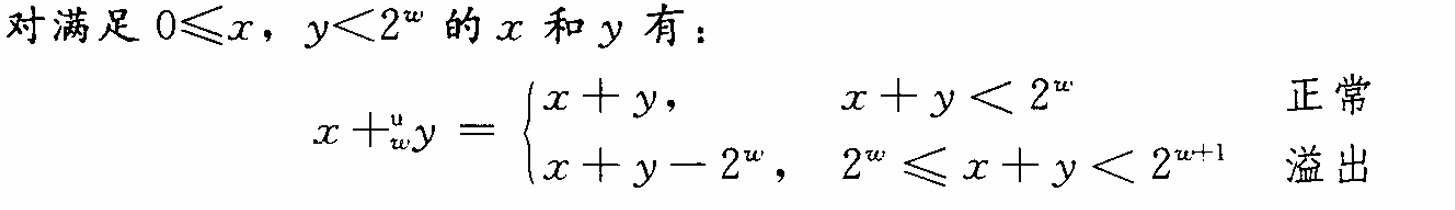
在正常情况下,和w + 1 位表示中的最高位会等于0,因此丢弃它不会改变这个数值。但是当他的结果超过范围时,和的w+1 位 表示中的最高位会等于1,因此丢弃它就相当于从和中减去 了2的w次方。
说一个算术运算溢出,是指完整的整数结果不能放到数据类型的字长限制中去。
当执行C程序时,不会将溢出作为错误而发信号。不过有的时候,我们可能希望判定 是否发生了溢出。对于无符号整数,正常情况下两个数的求和的结果是一定大于任意一个数的。当发现求出的和出现小于时就应该时发生了溢出。
2.3.2 补码加法
对于补码加法,我们必须确定当结果太大(为正)或者太小(为负)时,应该做些什么。
运算规则如下:

当发生正溢出时,结果会被截断为与原始位数相同的位数,丢失了溢出的高位。
假设我们有两个正数 +127 和 +2,它们的补码分别为0111 1111和 0000 0010,将它们相加得到1000 0001,对应十进制数为 -127。是由于这个结果超出了8位补码能够表示的范围(-128 到 127),因此发生了正溢出。
当负溢出发生时,结果会被截断为与原始位数相同的位数,丢失了溢出的高位。
假设我们有两个负数 -128 和 -1,它们的补码分别为1000 0000 和1111 1111,将它们相加得到0111 1111,对应十进制数为 +127。是由于这个结果超出了8位补码能够表示的范围(-128 到 127),因此发生了负溢出。
2.3.3 补码的非
补码的非操作是指对一个补码数的每一位取反(0变为1,1变为0),然后再加1。它的作用是将一个有符号整数变为它的相反数。
2.3.4 无符号乘法
将一个无符号数截断为w位等价于计算该值摸2的w次方,得到:
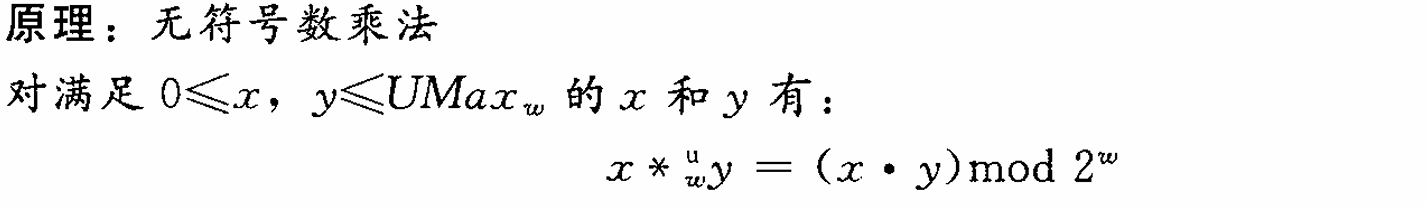
2.3.5 补码乘法
将一个补码数截断为w位相当于先计算该值模2的w次方,再把无符号数转换为补码,得到:

2.3.6 乘以常数
以往,在大多数机器上,整数乘法指令相当慢,需要10个或者更多的时钟周期,然 而其他整数运算(例如加法、减法、位级运算和移位)只需要1个时钟周期。因此,编译器使用 了一项重要的优化,试着用移位和加法运算的组合来代替乘以常数因子的乘法。
首先,我们会考虑乘以2的幂的情况。
一个无符号整数乘以2的w次方,相当于左移w个二进制位 。
对于其他数字例如,假设一个程序包含表达式x * 14。利 用14=2^3+2^2+2^1],编译器会将乘法重写为(x<<3)+(x<<2)+(x<<l),将一个乘法替换为三个移位和两个加法。
2.3.7 除以2的幂
在大多数机器上,整数除法要比整数乘法更慢—需要30个或者更多的时钟周期。 除以2的幂也可以用移位运算来实现,只不过我们用的是右移,而不是左移。无符号和补 码数分别使用逻辑移位和算术移位来达到目的。
2.4 浮点数
浮点表示对形如V=xX2^y的有理数进行编码。它对执行涉及非常大的数字、非常接近于0的数字,以及更普遍地作为实数运算的近似值的计算,是很 有用的。
2.4.1 二进制小数
理解浮点数的第一步是考虑含有小数值的二进制数字。首先,让我们来看看更熟悉的 十进制表示法。
例如:
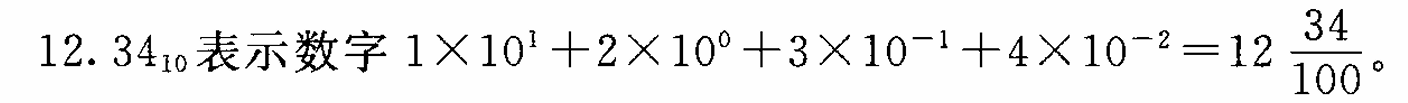
现在换成二进制表示,例如:
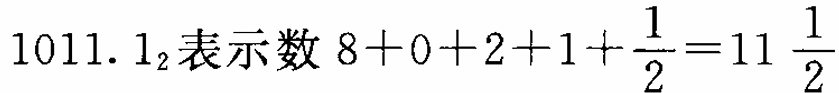
其中,二进制小数点向左移动一位相当于这个数被2除,二进制小数点向右移动一位相当于将该 数乘2。
小数的二进制表示法只能表示那些能够被写成x X 2^y 的数。其他的值只能够被 近似地表示。例如,数字 1/5 可以用十进制小数0.20精确表示。不过,我们并不能把它准确地表示为一个二进制小数,我们只能近似地表示它,增加二进制表示的长度可以提高表示的精度。
2.4.2 IEEE浮点表示
由于定点表示法不能很有效地表示非常大的数字。例如,表达式5X2^100是 用101后面跟随100个零的位模式来表示。相反,我们希望通过给定x和j的值,来表示 形如:rX2> 的数。

符号(sign) s决定这数是负数(S=l)还是正数(S=0),而对于数值0的符号位解释 作为特殊情况处理。
尾数(significand) M是一个二进制小数,它的范围是1~2—e,或者是0 ~1—e。
阶码(exponent) E的作用是对浮点数加权,这个权重是2的£ :次幂(可能是负数)。
2.4.3舍入
因为表示方法限制了浮点数的范围和精度,所以浮点运算只能近似地表示实数运算。 因此,对于值工,我们一般想用一种系统的方法,能够找到 “最接近的” 匹配值:c',它可 以用期望的浮点形式表示出来。这就是舍入(rounding)运算的任务。
IEEE 浮点格式定义了四种不同的舍入方式。默认的方法是找到最接近的匹配,而其他三种可用 于计算上界和下界。

向偶数舍人方式采用的方法是:它将数字向上或者向下舍人,使得结果的最低有效数字是偶数。
向偶数舍人法能够运用在二进制小数上。我们将最低有效位的值0认为是偶数,值1认为是奇数。
2.4.4 浮点运算
IEEE 标准指定了一个简单的规则,来确定诸如加法和乘法这样的算术运算的结果。 把浮点值:r和看成实数,而某个运算©定义在实数上,计算将产生尺0«« (工©30,这是 对实际运算的精确结果进行舍人后的结果。
IEEE 标准中指定浮点运算行为方法的一个优势在于,它可以独立于任何具体的硬件或 者软件实现。因此,我们可以检查它的抽象数学属性,而不必考虑它实际上是如何实现的。
2.4.5 C语言中的浮点数
所有的C语言版本提供了两种不同的浮点数据类型:float和double。在支持IEEE浮点 格式的机器上,这些数据类型就对应于单精度和双精度浮点。另外,这类机器使用向偶数舍人 的舍人方式。不幸的是,因为C语言标准不要求机器使用IEEE浮点,所以没有标准的方法来 改变舍人方式或者得到诸如-0 、正无穷、负无穷或者NaN之类的特殊值。
当在int、float和 double格式之间进行强制类型转换时,程序改变数值和位模式 的原则如下(假设int是64位的):
从int转换成float:数字不会溢出,但可能会被舍入。由于float的精度较低,一些较大的整数值可能会丢失精度。
从int或float转换成double:double有更大的范围和更高的精度,因此能够保留精确的数值。转换过程中不会发生溢出。
从double转换成float:由于float的范围较小,double的值可能会溢出成正无穷或负无穷。此外,由于精度较低,double的值可能会被舍入。
从float或double转换成int:值将会向零舍入。在64位情况下,如果浮点数的值超出了int能表示的范围,转换结果将会是未定义的行为,可能会产生不可预测的结果。


)



)


:使用wails做桌面应用开发,使用gin+go-chatglm.cpp进行本地模型运行,在windows上运行成功)



 应用可以使用 PostgreSQL 作为向量数据库组件吗?)





