卷积神经网络(Convolutional Neural Network, CNN)是一类包含卷积计算且具有深度结构的前馈神经网络(Feedforward Neural Networks),主要用于图像识别、语音识别和自然语言处理等任务,是深度学习(deep learning)的代表算法之一。
卷积神经网络(Convolutional Neural Networks,CNN)是一种专门用来处理具有类似网格结构的数据的神经网络。例如时间序列数据(可以认为是在时间轴上有规律地采样形成的一维网格)和图像数据(可以看作是二维的像素网格)。卷积网络是指那些至少在网络的一层中使用卷积运算来替代一般的矩阵乘法运算的神经网络。因此,卷积神经网络具有表征学习(representation learning)能力,能够按其阶层结构对输入信息进行平移不变分类(shift-invariant classification)。
卷积神经网络结构一般由输入层(Input)、卷积层(Convolution)、池化层(Pooling)、全连接层(Fully Connected)组成。
1. 传统神经网络与卷积神经网络的区别

首先我们探讨一下传统神经网络与卷积神经网络的区别。上图是传统神经网络和卷积神经网络的简单结构示意图,关于传统神经网络的基本内容,可以详见我之前的文章:神经网络1-基础过关。我们从上图可以直观的发现卷积神经网络和传统神经网络相比,有如下区别:
- 输入数据的维度:传统神经网络的输入通常是一个向量,即一维数据。而卷积神经网络的输入则是一个三维的长方体矩阵,例如H×W×3,其中H表示高度,W表示宽度,3则表示颜色通道(红色、绿色和蓝色)。这种不同的输入方式导致了神经网络的权重参数和输出结果也有很大的差异。
- 网络结构:传统神经网络的结构可能相对简单,通常不包含卷积和池化这样的特殊层。而卷积神经网络则包含四层结构:输入层、卷积层、池化层和全连接层。其中,卷积层负责对上一层的结果进行卷积运算,提取特征;池化层则对上一层结构进行池化,压缩特征;全连接层则起到了“分类器”的作用。
- 运算方式:传统神经网络的运算方式主要是叉积矩阵乘法运算(一维),而卷积神经网络则采用的是点积矩阵卷积运算(多维)。
传统神经网络和卷积神经网络在输入数据的维度、网络结构以及运算方式等方面都存在明显的差异。这些差异使得卷积神经网络在处理图像等具有网格结构的数据时具有更高的效率和准确性。
2. 卷积神经网络的架构

卷积神经网络的架构通常由四层结构组成:输入层、卷积层、池化层和全连接层。其中,
- 输入层:这是卷积神经网络的第一层,负责接收原始图像数据。输入层的尺寸通常与原始图像的尺寸相同,颜色通道数可以是1(灰度图像)或3(彩色图像)。
- 卷积层:卷积层是卷积神经网络中的核心层,负责通过卷积运算提取图像的特征。卷积操作是通过卷积核(Filter)与输入信号进行卷积运算而完成的,每个卷积核可以提取一种特定的特征。在卷积层中,可以设置多组卷积核,每组卷积核可以提取不同的特征。卷积层的输出通常会通过激活函数进行激活,常用的激活函数有ReLU、Sigmoid、Tanh等。
- 池化层:池化层是卷积神经网络中的另一个重要层级,它的主要作用是对卷积层的输出进行下采样,从而减少参数数量,提高模型计算效率。池化层通常采用最大池化或平均池化操作。最大池化是指从池化窗口中选择最大值作为输出,而平均池化是指从池化窗口中取平均值作为输出。池化层通常不改变通道数量,但可以减少特征图的尺寸。
- 全连接层:全连接层是卷积神经网络的最后一层,通常用来输出最终的分类结果。全连接层将所有的特征连接在一起,通过全连接层的权重计算来预测输出结果。在全连接层中,通常会使用Softmax或Sigmoid函数进行激活。
除了以上四种类型的层,卷积神经网络还可能包含其他类型的层,如激活层、BN(Batch Normalization,批归一化)层、损失层等。这些层的引入可以进一步提高模型的性能和稳定性。请注意,以上只是卷积神经网络的一种常见架构,实际上,根据不同的任务和数据集,卷积神经网络的架构可能会有所不同。例如,一些网络可能包含多个并行的卷积路径(如Inception系列网络),或者采用残差连接(如ResNet系列网络)等技巧来改善模型的性能。
3. 什么是卷积?
卷积(Convolution)是一种特殊的线性变换,它通过在输入数据上滑动卷积核(也称为滤波器)来进行计算。卷积核是一个小的二维矩阵,通常与输入数据的局部区域进行点乘运算,然后将结果汇总得到一个新的值。这个过程也被称为滤波(Filter)。卷积核在输入数据上进行滑动,每次计算与卷积核重叠部分的点乘和,从而得到一个新的特征图(Feature Map)。如下图所示:

在上图中,我们从原始的图像数据中提取了一个5x5的图像数据用来进行卷积操作,卷积核设置为
我们利用上述的卷积核在5x5的图像数据中进行滑动计算,将滑动到的图像原始数据与卷积核进行点乘运算,计算出卷积核在该位置上获取的新特征。例如图中,卷积核滑动到左下角,那么左下角的原始图像数据与卷积核进行点乘运算,计算出新特征为9。具体计算过程如下:
卷积操作可以提取输入数据的局部特征,实现特征的共享和抽象。通过多个卷积核的并行操作,可以提取不同类型的特征,形成更加复杂的特征表示。卷积操作具有平移不变性(Translation Invariance),即无论输入数据中的特征出现在哪个位置,卷积操作都能提取到相同的特征。这使得卷积神经网络在处理图像等具有网格结构的数据时具有很高的效率和准确性。
卷积神经网络中的卷积操作与图像处理中的卷积运算有相似之处,但也有一些不同之处。在卷积神经网络中,卷积核通常是可学习的参数,通过反向传播算法进行更新。而在图像处理中,卷积核通常是固定的,用于实现特定的滤波效果。总的来说,卷积是卷积神经网络中的核心操作之一,它负责提取输入数据的局部特征,并通过多层卷积操作形成复杂的特征表示。这些特征表示随后会被送入全连接层进行分类或回归等任务。
4. 图像的颜色通道
图像的颜色通道是指在数字图像处理中,描述图像颜色信息的组成部分。对于彩色图像,颜色通道通常分为红色、绿色和蓝色三个通道,分别对应RGB颜色模型中的R、G、B三个分量。这三个通道叠加在一起,可以显示出各种颜色。除了RGB颜色模型外,还有其他颜色模型,如CMYK、HSV等,但RGB是工业界最常用的一种颜色标准。

在数字图像处理中,每个颜色通道都可以看作是一个灰度图像,即每个通道只有一个采样颜色的图像。因此,对于彩色图像,其颜色通道数通常为3,即RGB三个通道。而对于灰度图像,其颜色通道数只有1,即只有一个灰度通道。
5. 彩色图像在卷积神经网络中的表示
图像的颜色通道是描述图像颜色信息的重要组成部分,对于彩色图像的处理和分析具有重要意义。在卷积神经网络中,对于彩色图像的输入,通常会将其看作是一个三维的长方体矩阵,其中高度和宽度对应图像的大小,而颜色通道数则对应图像的深度。

卷积层中的卷积核也会针对每个颜色通道进行卷积运算,从而提取出不同通道上的特征。在全连接层中,则会将所有通道上的特征进行汇总,从而进行最终的分类或回归任务。

6. 彩色图像的卷积运算
在卷积神经网络中,针对每个颜色通道进行卷积运算可以提取出更加丰富的特征信息,从而提高模型的性能和准确性。我们以下图为例,来解释彩色图像的卷积操作。

在上图中,我们从彩色图像中提取了一个7x7x3的图像片段。从图中我们可以看到,在卷积神经网络中,我们提取的3通道图像数据最后是分成了三个小矩阵来进行表示的。这意味着,我们处理的是几通道的数据,就会产生几通道的矩阵数据。如果我们是处理的一副灰度图,其颜色通道为1,相应的图像数据矩阵就只有1个。
我们设置了一个3x3x3的卷积核来进行卷积运算。需要注意的是,我们的卷积核的组成个数,也就是3x3x3中最后一个3,应该与图像的通道数保持一致。如果我们是处理的一副灰度图,其颜色通道为1,那么我们的卷积核就相应的要修正为3x3x1。而卷积核中前面的3x3,表示每个卷积核的大小。设置好卷积核之后,我们就开始采用滑动窗口的方式对图像数据进行点乘运算。具体的运算规则就是矩阵对应的数值先相乘,再相加。我们在上文中已经举例进行了说明。最后,我们将3个通道经过卷积运算之后获得的新特征进行相加,再加上一个偏置项就获得了这一次滑动窗口的特征值。设置偏置项
的目的是为卷积运算提供一个可学习的常数偏移量。
在卷积运算中,每个卷积核都会在输入数据的局部区域上进行滑动,并与该区域进行点乘运算。然后,将点乘运算的结果加上偏置项b,得到该局部区域的卷积输出。偏置项b是一个可学习的参数,通过反向传播算法进行更新,它可以使得卷积神经网络在训练过程中更好地适应输入数据的分布,从而提高模型的性能和准确性。

经过每个卷积核的卷积运算之后,我们可以获得一张特征图(特征矩阵)。当然,我们也可以设置多个卷积核,这样我们就可以使用同一个图像数据计算出多张特征图。当我们想在这一轮的特征图上继续进行卷积运算,下一轮卷积使用的卷积核的组成个数也相应的需要进行修改。例如,假如我们在这一轮卷积运算中,我们使用了6个不同的卷积核得到了6张特征图,那么在下一轮卷积操作中,相当于原始数据变成了6通道数据,因此卷积核的组成个数就变成了6个,如上图所示。同样需要注意的是,在同一轮卷积操作中,卷积核的大小必须保持一致。不同轮次的卷积操作中,卷积核的大小可以不一样。
7. 卷积核几个关键参数
卷积核的大小、步幅(Stride)和填充(Padding)等参数会影响卷积操作的结果。卷积核的大小决定了感受野(Receptive Field)的大小,即卷积核能够覆盖的输入数据的范围。步幅决定了卷积核在输入数据上滑动的步长,而填充则用于控制输出特征图的大小。
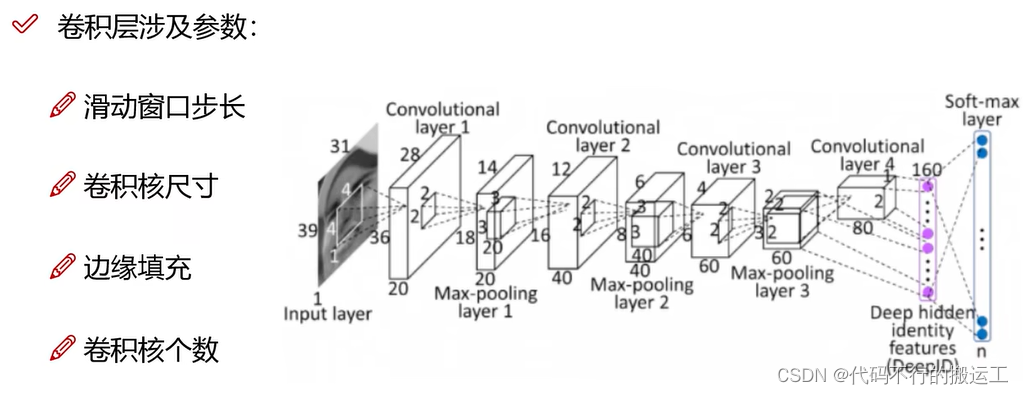
7.1 步幅(步长)
卷积核的步幅是卷积神经网络中一个重要的超参数,它决定了卷积核在输入数据上的滑动步长,从而影响了模型的性能和计算效率。卷积核的步幅(Stride)是指在卷积神经网络中,卷积核在输入数据上滑动时每次移动的像素距离。步幅定义了卷积核遍历图像时的步长大小,它决定了卷积核每次移动多远来进行下一次的卷积运算。

步幅的大小会影响卷积运算的结果和输出特征图的尺寸。在卷积神经网络中,步幅通常设置为1或2。当步幅为1时,卷积核每次移动一个像素距离;当步幅为2时,卷积核每次移动两个像素距离,因此最终形成的特征图的大小完全不同。如上图所示,同样是7x7的图像数据,当我们采用步幅为1时,生成的特征图为5x5的矩阵,而当我们采用步幅为2时,生成的特征图为3x3的矩阵。
较小的步幅可以保留更多的输入信息,但可能会增加计算量和模型的参数数量。而较大的步幅则会减少输出特征图的尺寸,加快计算速度,但可能会丢失一些输入信息。因此步幅的设置需要根据具体的任务和数据集进行调整,以达到最佳的模型性能和计算效率。
7.2 卷积核的尺寸
在卷积神经网络中,卷积核的尺寸是一个重要的超参数,需要根据具体的任务和数据集进行调整。卷积核的尺寸是指卷积核的长和宽的维度大小,通常表示为卷积核的高度和宽度,例如3x3、5x5等。这个尺寸决定了卷积核能够覆盖的输入数据的范围,也影响了卷积操作对输入数据的感受野大小。较小的卷积核尺寸(如3x3)可以减少模型的参数数量和计算量,加快训练速度,并且可以通过增加卷积层的深度来扩大感受野,从而捕获更多的空间信息。而较大的卷积核尺寸(如5x5或更大)可以覆盖更大的输入区域,直接捕获更多的上下文信息,但可能会增加模型的复杂度和计算量。
此外,卷积核的尺寸通常是奇数x奇数,如3x3、5x5、7x7等。这是因为奇数尺寸的卷积核有一个中心点,可以更好地定位特征的位置。
7.3 感受野
卷积操作对输入数据的感受野(Receptive Field)指的是卷积神经网络中每个网络层输出的特征图(Feature Map)上的像素点在输入图片上映射的区域大小。换句话说,感受野是输入数据中被卷积核所覆盖和影响的区域。

在卷积神经网络中,随着卷积层的加深,每个输出节点的感受野会逐渐增大,即每个输出节点所依赖的输入数据的区域范围会逐渐扩大。这是因为每一层的卷积操作都会将前一层的局部感受野扩展为自己的感受野,而卷积核的大小和步幅则决定了这种扩展的速度和范围。

感受野的大小对于卷积神经网络的性能有很大的影响。较大的感受野可以使得模型更好地捕获输入数据的全局信息,提高模型的泛化能力;而较小的感受野则可能限制了模型的视野,使得模型只能关注到输入数据的局部信息,从而影响模型的性能。因此,在设计卷积神经网络时,需要根据具体的任务和数据集来选择合适的卷积核尺寸、步幅和深度等超参数,以使得模型能够具有适当的感受野大小和覆盖范围,从而取得最佳的性能表现。
7.4 边缘填充
卷积操作的边缘填充(Padding)是指在卷积神经网络中,对输入数据的边界进行额外的像素填充,以控制输出特征图的大小和形状。在卷积操作中,由于卷积核的大小和步幅的存在,可能会导致输出特征图的尺寸小于输入数据。为了解决这个问题,可以在输入数据的边界周围添加额外的像素值,通常是0,以增加输入数据的尺寸,从而使得输出特征图的尺寸与输入数据相同或更大。如下图的图像数据中的灰色0部分。

边缘填充的作用主要有两个方面:
- 控制输出特征图的大小和形状:通过填充,可以使得输出特征图的尺寸与输入数据相同或更大,从而保持空间信息的连续性,并且方便后续的网络层进行进一步的处理。
- 充分利用边缘信息:在卷积操作中,越靠近图片边缘的像素点被卷积计算的次数越少,这可能会导致边缘信息的丢失。通过填充,可以将边缘像素点扩展到卷积核的覆盖范围内,从而充分利用边缘信息,提高模型的性能。
边缘填充的方式有多种,常见的包括零填充(Zero Padding)和边缘复制(Edge Replication)等。零填充是在输入数据的边界周围填充0像素,而边缘复制则是将输入数据的边缘像素复制到边界区域。选择哪种填充方式取决于具体的任务和数据集。
7.5 卷积核的个数
卷积核的个数是指在卷积神经网络中,每一层卷积层所使用的卷积核的数量。这个数量决定了该层卷积操作后输出的特征图的数量,也就是说,每一个卷积核都会生成一个对应的特征图。
卷积核的个数通常是根据具体任务和数据集的特点进行设置的。增加卷积核的个数可以使得模型学习到更多的特征,提高模型的表达能力;但同时也会增加模型的参数数量和计算复杂度,可能导致过拟合和训练困难的问题。
在卷积神经网络中,每一层的卷积核个数通常是根据经验或者通过实验来确定的。在一些经典的卷积神经网络结构中,如LeNet、AlexNet、VGGNet等,都会给出每一层卷积核的个数作为参考。同时,一些自动化设计卷积神经网络的方法,如NAS(Neural Architecture Search)等,也可以自动搜索每一层卷积核的最优个数。
7.6 输出特征图的大小计算公式


卷积共享参数是指在卷积神经网络中,多个卷积核在卷积运算过程中共享同一组参数。换句话说,对于输入数据的不同位置,使用相同的卷积核进行卷积操作,从而减少了参数的数量。这种参数共享的方式不仅减少了模型参数的数量,降低了模型的复杂度,还使得模型具有平移等变性,即对于输入数据的平移变换,模型的输出不会发生变化。这种参数共享的机制是卷积运算的固有属性,也是卷积神经网络能够在大规模数据集上成功应用的关键因素之一。

需要注意的是,虽然参数共享可以减少模型参数的数量,但并不意味着所有的卷积核都会学习到相同的特征。在训练过程中,每个卷积核都会根据输入数据的不同特点进行学习和调整,从而学习到不同的特征表示。因此,尽管参数共享,但每个卷积核仍然具有其独特的作用和意义。
8. 池化层
卷积神经网络的池化层(Pooling Layer)是卷积神经网络中的一个重要组成部分,它的主要作用是对卷积层输出的特征图进行下采样(Downsampling),以减小特征图的尺寸,从而减少模型的参数数量、计算量以及过拟合的可能性。
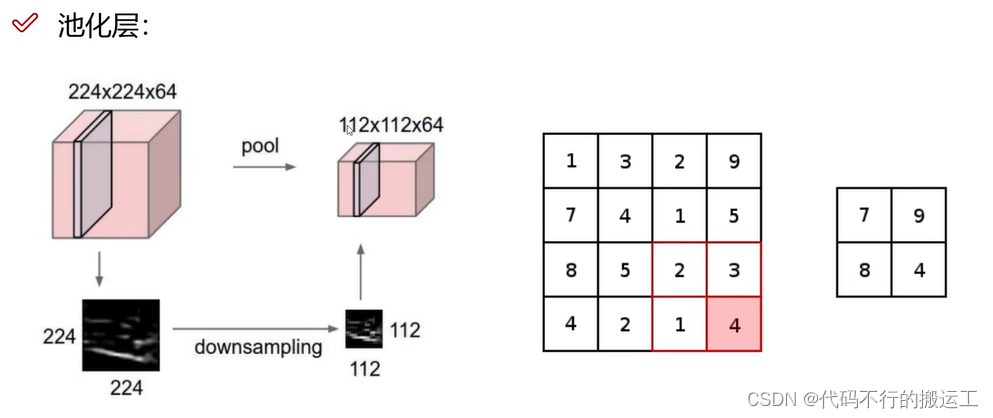
池化层通常位于卷积层之后,对卷积层输出的特征图进行空间上的下采样。最常见的池化操作包括最大池化(Max Pooling)和平均池化(Average Pooling)。最大池化是在每个池化窗口内选择最大的像素值作为输出,而平均池化则是计算每个池化窗口内像素值的平均值作为输出。这些池化操作都是对局部区域进行的,因此可以有效地降低特征图的维度。

池化层的作用主要有以下几点:
- 特征降维:通过池化操作,可以将特征图的尺寸减小,从而减少模型的参数数量和计算量,提高模型的计算效率。
- 特征不变性:池化操作可以使模型对输入数据的微小变化具有一定的鲁棒性,即模型对于输入数据的平移、旋转等变换具有一定的不变性。
- 防止过拟合:通过减小特征图的尺寸,池化层可以降低模型的复杂度,从而在一定程度上防止过拟合的发生。
需要注意的是,池化层虽然可以降低模型的计算量和参数数量,但也会丢失一些空间信息。因此,在设计卷积神经网络时,需要权衡池化层的作用和可能带来的信息损失,选择合适的池化方式和池化窗口大小。
9. 全连接层
 卷积神经网络结构一般由输入层(Input)、卷积层(Convolution)、池化层(Pooling)、全连接层(Fully Connected)组成。一般我们是在两个卷积层之后添加一个池化层。每一层的确定主要是以是否存在需要反向调整的参数为准。因此Relu和池化不算一层,卷积层和全连接层算一层。
卷积神经网络结构一般由输入层(Input)、卷积层(Convolution)、池化层(Pooling)、全连接层(Fully Connected)组成。一般我们是在两个卷积层之后添加一个池化层。每一层的确定主要是以是否存在需要反向调整的参数为准。因此Relu和池化不算一层,卷积层和全连接层算一层。

当我们学习到足够的特征之后,我们需要将三维的特征图给变换为一维的特征向量,然后根据需要进行全连接运算,获得最终的分类结果。
10. 残差网络Resnet
残差网络(ResNet)是一种深度卷积神经网络,由微软研究院的何凯明等人于2015年提出。ResNet通过引入残差连接(residual connection)来解决深度网络中的梯度消失问题,从而极大地提升了网络的训练效率和性能。
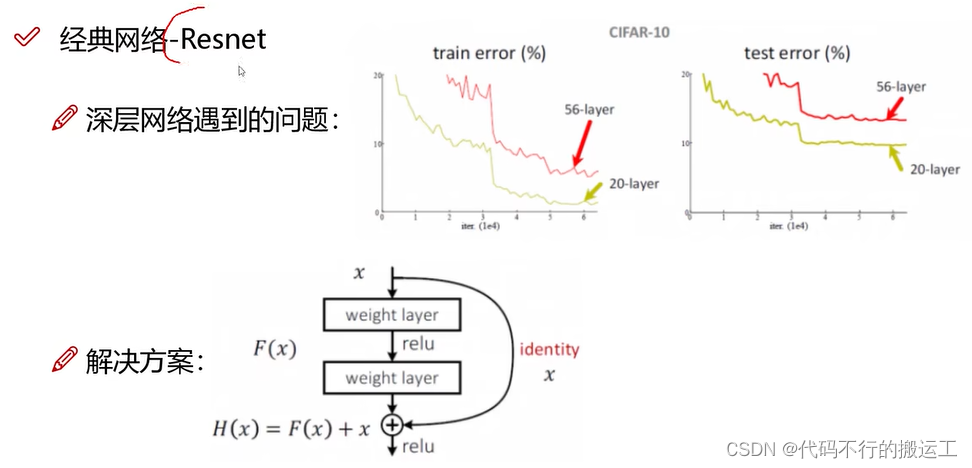
在ResNet中,每个残差块(Residual Block)都包含多个卷积层,并且在输入和输出之间添加了一个恒等映射(identity mapping)。这个恒等映射使得网络可以更容易地学习输入和输出之间的残差(即差异),而不是直接学习输出。通过这种方式,ResNet可以成功地训练出非常深的网络,而不会出现梯度消失或梯度爆炸的问题。
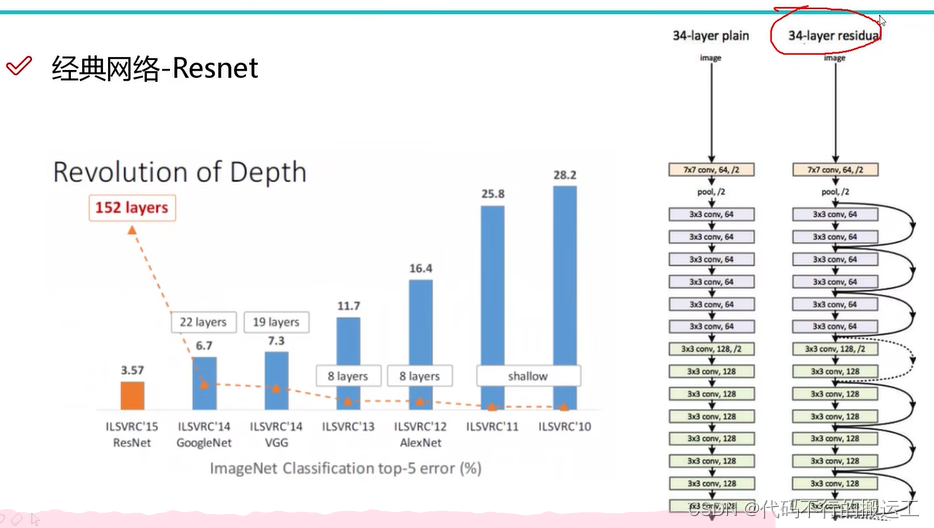
ResNet的结构可以极大地加速超深神经网络的训练,并且模型准确率也有非常大的提升。在2015年的ILSVRC比赛中,ResNet夺得了冠军,证明了其强大的性能。此后,残差连接的思想被广泛应用于各种深度学习任务中,成为了深度学习领域的一个重要里程碑。

















)

