字符串（算法竞赛）--字典树Trie与最大异或对

1、B站视频链接：F06 字典树(Trie)_哔哩哔哩_bilibili

题目链接：【模板】字典树 - 洛谷

#include <bits/stdc++.h> 
using namespace std;
const int N=100010;
int n;
char s[N];
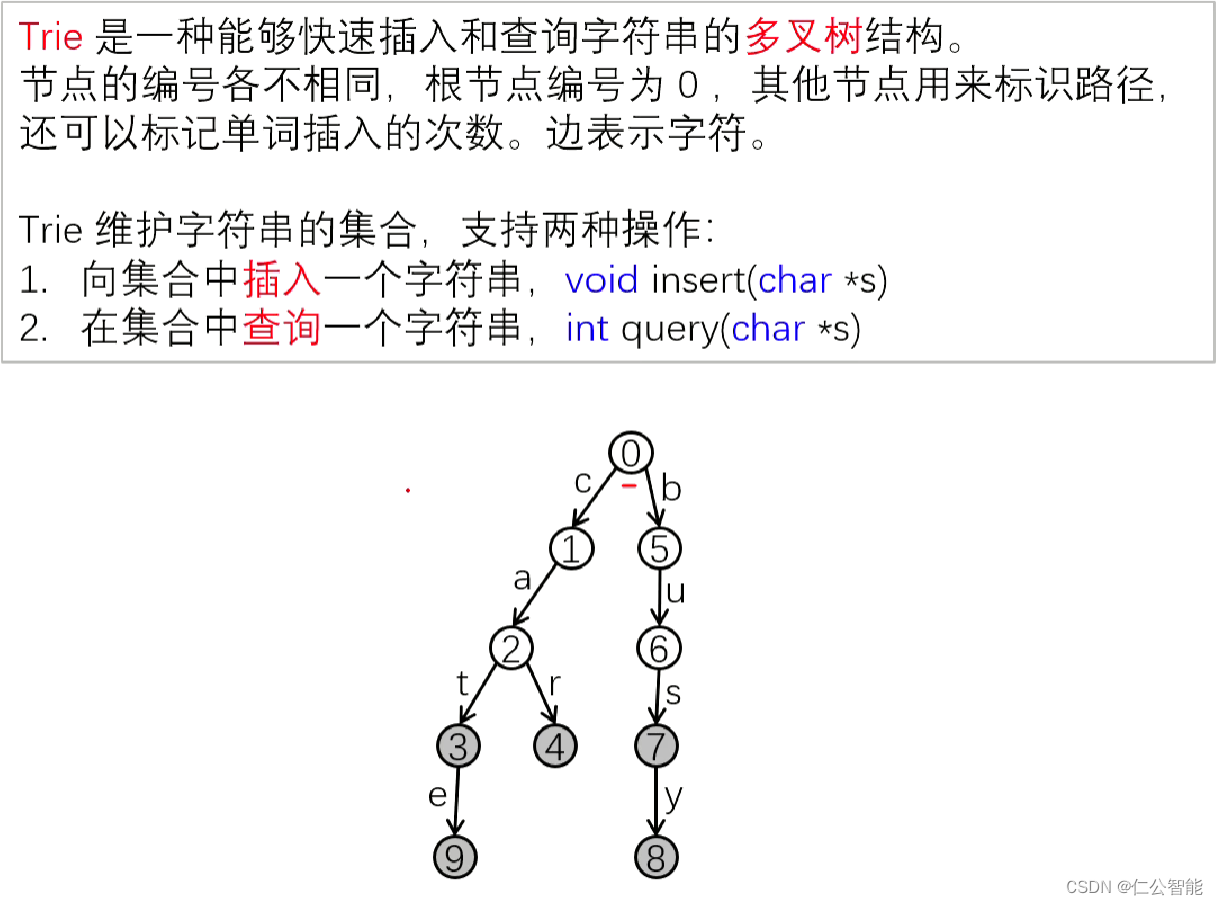
int ch[N][26];//ch[0][2]=1表示0号节点通过c边走到了节点1 
int cnt[N],idx;//分别表示记录次数和节点编号 
void insert(char *s){int p=0;//从根节点0开始for(int i=0;s[i];i++){//将字符串的每个字母循环扫描 int j=s[i]-'a';//字母映射成对应的数字if(!ch[p][j])ch[p][j]=++idx;//如果未出现过，则创建新的节点p=ch[p][j];//新节点作为新的父节点 }cnt[p]++;//循环结束，单词次数加一 
}
int query(char *s){int p=0;for(int i=0;s[i];i++){int j=s[i]-'a';if(!ch[p][j])return 0;//不存在则直接返回p=ch[p][j];//一直向下找 }return cnt[p];
}
int main(){scanf("%d",&n);while(n--){char op;scanf("%s %s",&op,&s);if(op=='I')insert(s);else printf("%d\n",query(s));}return 0;
}

题目链接：1、[JSOI2009] 电子字典 - 洛谷

2、[JSOI2015] 字符串树 - 洛谷

3、[AGC057C] Increment or Xor - 洛谷

4、[省选联考 2020 A 卷] 树 - 洛谷

2、B站视频链接：F07 最大异或对（01Trie）_哔哩哔哩_bilibili

#include <bits/stdc++.h> 
using namespace std;
const int N=100010;
int n,a[N];
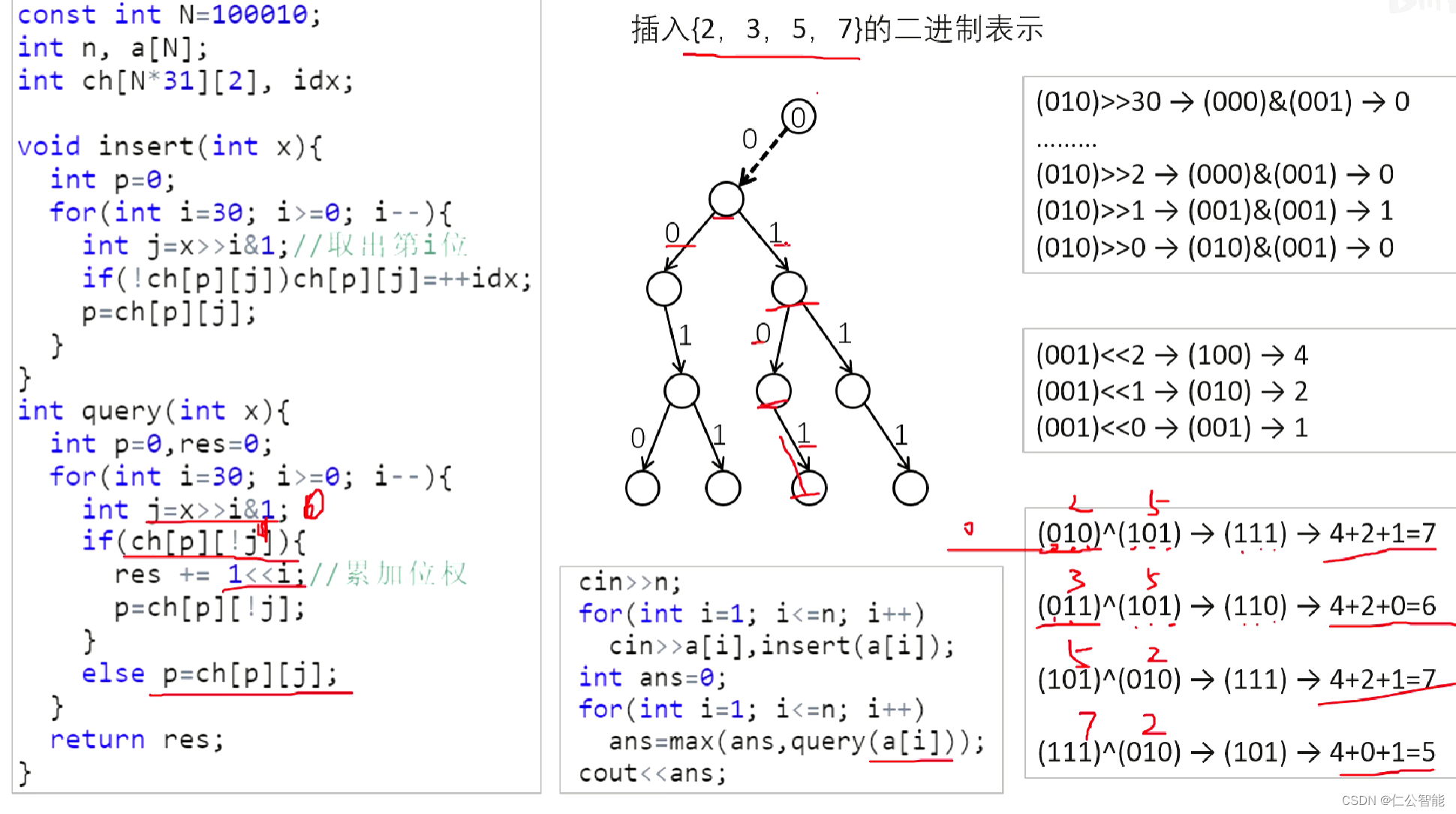
int ch[N*31][2],idx;//最多走31层，二叉树
void insert(int x){int p=0;for(int i=30;i>=0;i--){int j=x>>i&1;//取出第i位if(!ch[p][j])ch[p][j]=++idx;p=ch[p][j]; }
}
int query(int x){int p=0,res=0;for(int i=30;i>=0;i--){int j=x>>i&1;if(ch[p][!j]){//异或运算尽量走不通的路值更大 res+=1<<i;//累加位权p=ch[p][!j]; }else p=ch[p][j];}return res;
}
int main(){cin>>n;for(int i=1;i<=n;i++){cin>>a[i],insert(a[i]);}int ans=0;for(int i=1;i<=n;i++){ans=max(ans,query(a[i]));}cout<<ans;return 0;
}