目录
算法思路
Dijkstra求最短路
AcWing 849. Dijkstra求最短路 I - AcWing
850. Dijkstra求最短路 II - AcWing题库
最短路
最短路 - HDU 2544 - Virtual Judge (vjudge.net)
【模板】单源最短路径(弱化版)
P3371 【模板】单源最短路径(弱化版) - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
【模板】单源最短路径(标准版)
P4779 【模板】单源最短路径(标准版) - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
畅通工程续
畅通工程续 - HDU 1874 - Virtual Judge (vjudge.net)
算法思路
dijkstra解决的是单源的最短路问题,就是一个顶点到其他顶点的最短路问题
开一个数组dist,dist[x]表示从起点出发,到x的距离
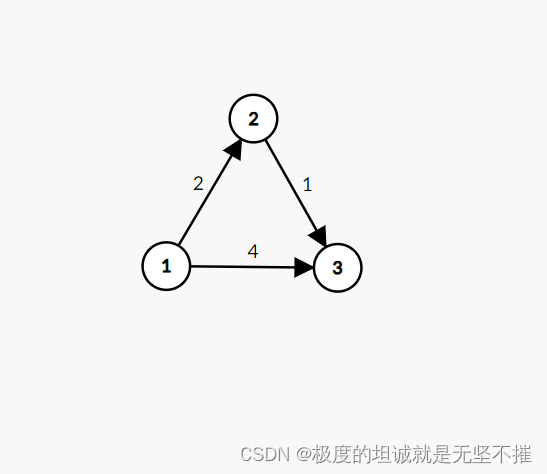
比如这幅图,初始情况下,把所有的dist都设置为inf(也就是无穷大)
dist[1]=0,dist[2]=dist[3]=inf
因为1是起点,自己到自己的距离是0
还有一个bool类型的vis数组,因为每个点只能走一次
选当前离起点最近(权值最小)且没有选过的点,来更新其它点的距离
所以如图:
第一次选1号,更新最近的2,3号点 dist[2]=2,dist[3]=4
第二次选2号(因为权值比1到3的小) dist[2]+1<dist[3],所以dist[3]=dist[2]+1
这个样例的最短路就得到了
Dijkstra求最短路
AcWing 849. Dijkstra求最短路 I - AcWing
850. Dijkstra求最短路 II - AcWing题库
这两道题只有数据范围的差别,用下面的代码可以一次过
注意:
优先队列q里面的pair存的是dist和点数
二维数组g里面的pair存的是点数和边权
完整代码:
#include <bits/stdc++.h>
#define int long long
const int N = 15e4+10;
std::vector<std::vector<std::pair<int,int>>> g(N);
#define PII std::pair<int,int>
signed main()
{int n,m;std::cin >> n >> m;for(int i = 1;i <= m;i ++){int u,v,w;std::cin >> u >> v >> w;g[u].push_back({v,w});}std::priority_queue<PII,std::vector<PII>,std::greater<>> q;std::vector<int> dist(n+1,INT_MAX);std::vector<bool> vis(n+1);dist[1]=0;q.push({0,1});//存dist和点数while(!q.empty()){auto node = q.top();q.pop();int cur=node.second;if(vis[cur]==true)continue;else{vis[cur]=true;for(int i = 0;i < g[cur].size();i ++){int e=g[cur][i].first;int w=g[cur][i].second;if(dist[e]>dist[cur]+w){dist[e]=dist[cur]+w;q.push({dist[e],e});}}}}if(dist[n]==INT_MAX)std::cout<<-1;elsestd::cout<<dist[n];return 0;
}最短路
最短路 - HDU 2544 - Virtual Judge (vjudge.net)
思路:dijkstra,但是需要建立双向边
注意:多组输入最好不要开全局变量,如果开全局变量记得清空
完整代码:
#include <bits/stdc++.h>
#define int long long
#define PII std::pair<int,int>
const int N = 1e4+10;
signed main()
{int n,m;while(std::cin >> n >> m){if(n==0&&m==0)break;std::vector<std::vector<std::pair<int,int>>>g (N+1);std::priority_queue<PII,std::vector<PII>,std::greater<>> q;std::vector<int> dist(n+1,INT_MAX);std::vector<bool> vis(n+1);dist[1]=0;for(int i = 1;i <= m;i ++){int u,v,w;std::cin >> u >> v >> w;g[u].push_back({v,w});g[v].push_back({u,w});}q.push({0,1});//存dist和点数while(!q.empty()) {auto node = q.top();q.pop();int cur = node.second;if (vis[cur] == true)continue;else {vis[cur] = true;for (int i = 0; i < g[cur].size(); i++) {int e = g[cur][i].first;//存点int w = g[cur][i].second;//存边权if (dist[e] > dist[cur] + w) {dist[e] = dist[cur] + w;q.push({dist[e], e});}}}}std::cout<<dist[n]<<"\n";}return 0;
}【模板】单源最短路径(弱化版)
P3371 【模板】单源最短路径(弱化版) - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
思路:dijkstra模板
完整代码:
#include <bits/stdc++.h>
#define int long long
#define PII std::pair<int,int>
const int N = 5e5+10;
signed main()
{int n,m,s;std::cin >> n >> m >> s;std::vector<std::vector<std::pair<int,int>>> g(n+1);std::vector<int> dist(n+1,INT_MAX);std::vector<bool> vis(n+1);dist[s]=0;for(int i = 1; i <= m;i ++){int u,v,w;std::cin >> u >> v >> w;g[u].push_back({v,w});}std::priority_queue<PII,std::vector<PII>,std::greater<>> q;q.push({0,s});//存dist和点数while(!q.empty()) {auto node = q.top();q.pop();int cur = node.second;if (vis[cur] == true)continue;else {vis[cur] = true;for (int i = 0; i < g[cur].size(); i++) {int e = g[cur][i].first;//存点int w = g[cur][i].second;//存边权if (dist[e] > dist[cur] + w) {dist[e] = dist[cur] + w;q.push({dist[e], e});}}}}for(int i = 1;i <= n;i ++){std::cout<<dist[i]<<" ";}return 0;
}【模板】单源最短路径(标准版)
P4779 【模板】单源最短路径(标准版) - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
和上一题的代码一样,只是数据范围大一点
完整代码:
#include <bits/stdc++.h>
#define int long long
#define PII std::pair<int,int>
const int N = 5e5+10;
signed main()
{int n,m,s;std::cin >> n >> m >> s;std::vector<std::vector<std::pair<int,int>>> g(n+1);std::vector<int> dist(n+1,INT_MAX);std::vector<bool> vis(n+1);dist[s]=0;for(int i = 1; i <= m;i ++){int u,v,w;std::cin >> u >> v >> w;g[u].push_back({v,w});}std::priority_queue<PII,std::vector<PII>,std::greater<>> q;q.push({0,s});//存dist和点数while(!q.empty()) {auto node = q.top();q.pop();int cur = node.second;if (vis[cur] == true)continue;else {vis[cur] = true;for (int i = 0; i < g[cur].size(); i++) {int e = g[cur][i].first;//存点int w = g[cur][i].second;//存边权if (dist[e] > dist[cur] + w) {dist[e] = dist[cur] + w;q.push({dist[e], e});}}}}for(int i = 1;i <= n;i ++){std::cout<<dist[i]<<" ";}return 0;
}畅通工程续
畅通工程续 - HDU 1874 - Virtual Judge (vjudge.net)
思路:用dijkstra,双向建边
完整代码:
#include <bits/stdc++.h>
#define int long long
#define PII std::pair<int,int>
signed main()
{int n,m;while(std::cin >> n >> m){std::vector<std::vector<PII>>g(n+1);std::vector<int> dist(n+1,INT_MAX);std::vector<bool> vis(n+1);std::priority_queue<PII,std::vector<PII>,std::greater<>> q;for(int i = 1;i <= m;i ++){int u,v,w;std::cin >> u >> v >> w;g[u].push_back({v,w});g[v].push_back({u,w});}int s,t;std::cin >> s >> t;dist[s]=0;q.push({0,s});//存dist和点数while(!q.empty()){auto node = q.top();q.pop();int cur=node.second;if(vis[cur]==true)continue;vis[cur]=true;for(int i = 0;i < g[cur].size();i ++){int e=g[cur][i].first;int w=g[cur][i].second;if(dist[e]>dist[cur]+w){dist[e]=dist[cur]+w;q.push({dist[e],e});}}}if(dist[t]==INT_MAX)std::cout<<-1<<"\n";elsestd::cout<<dist[t]<<"\n";}return 0;
}




)













