滤波作为自适应滤波系统中信号处理等研究领域的重要组成模块,主要被应用于信道均衡、系统识别、声学回波抵消、生物医学、雷达、波束形成等模块。在自适应滤波系统中,当信息数据统计方面的相关先验知识是已知的情况下,滤波器才能处理相关的输入信号,而只有所设计滤波器处理后的统计特性相致与输入信息的数据特征时,所对应匹配的滤波器才是最优的。而当信息的先验知识不可知时,普通滤波器已不再适用,这时需采用较为直接的方法:一是‘估计’,二是‘插入’;即先估计输入信号的先验知识或相关的统计特性,再将所得到的结果插入到运算公式中以便滤波器进行计算。而这个方法的实施需要精心制作,以及价格昂贵的硬件。
为了解决上述对普通滤波器应用的限制,改善其所存在的不足,就可采用自适应滤波器。主要是因为滤波器是通过自主设计并且可以自适应依赖递归算法进行全部的运算;采用这样的系统,可以在只得到有关信息的部分知识或者完全得不到有关信息先验知识的条件下,成功的完成滤波过程。而滤波算法作为核心模块,在自适应滤波器中,对算法的研发就显得尤为重要,它只需要某些预知的统计特性参数,就可以在一定程度上为滤波器完成所需要的工作。
在平稳环境下,自适应滤波器算法在成功迭代后能够在某种统计意义上收敛到最优的维纳解;在非平稳环境下,其还能为算法提供跟踪能力,因为只要输入滤波器的数据统计参数(或特性)的变化尽可能的缓慢,算法就能跟踪信息的统计特性,即跟踪其输入信号的变化的能力。
程序运行环境为MATLAB R2018,使用几种滤波自适应算法进行主动噪声消除,并且可迁移至金融时间序列,地震/微震信号,机械振动信号,声发射信号,电压/电流信号,语音信号,声信号,生理信号(ECG,EEG,EMG)等信号。几种滤波自适应算法包括:Filtered Least Mean Squares,Filtered Normalized Least Mean Squares,Filtered Recursive Least Squares,Least Mean Squares,Normalized Least Mean Squares,Recursive Least Squares等。
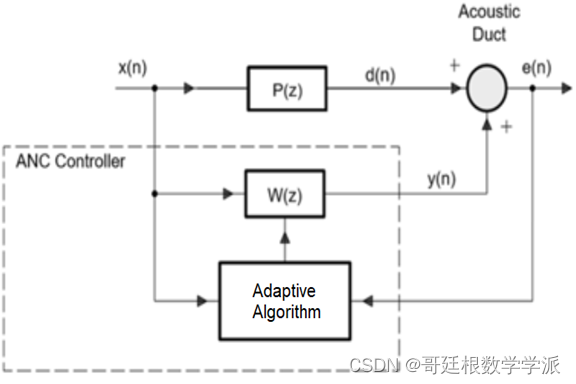
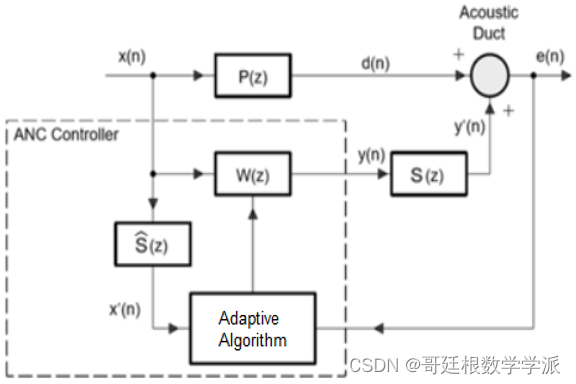
部分代码如下:
% Load data
load('data/speech') % load speech
load('data/noise') % load noise
load('data/bpir') % load filter
s = speech; % speech x(n)
x = noise; % noise
Pw = bpir; % filter P(z)
% Modes
sim_mode = true; % simulation mode
optpara_mode = true; % optimize parameters mode
ns_mode = true; % noisy speech demo出图如下:
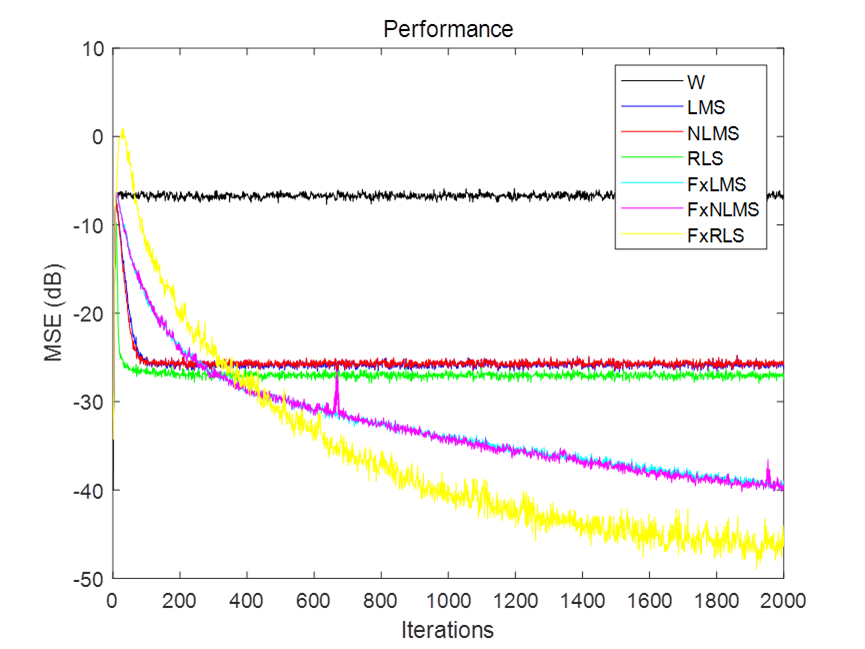
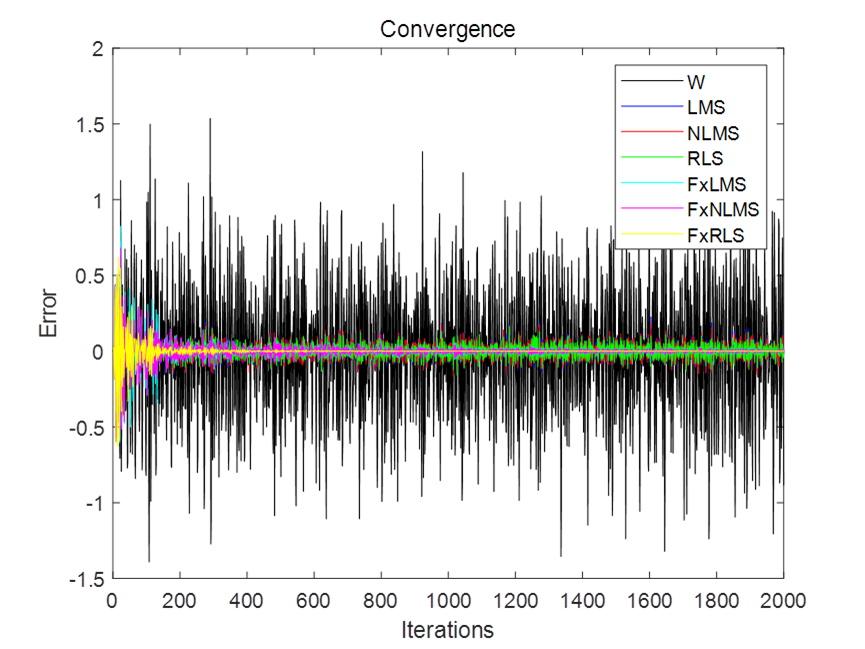
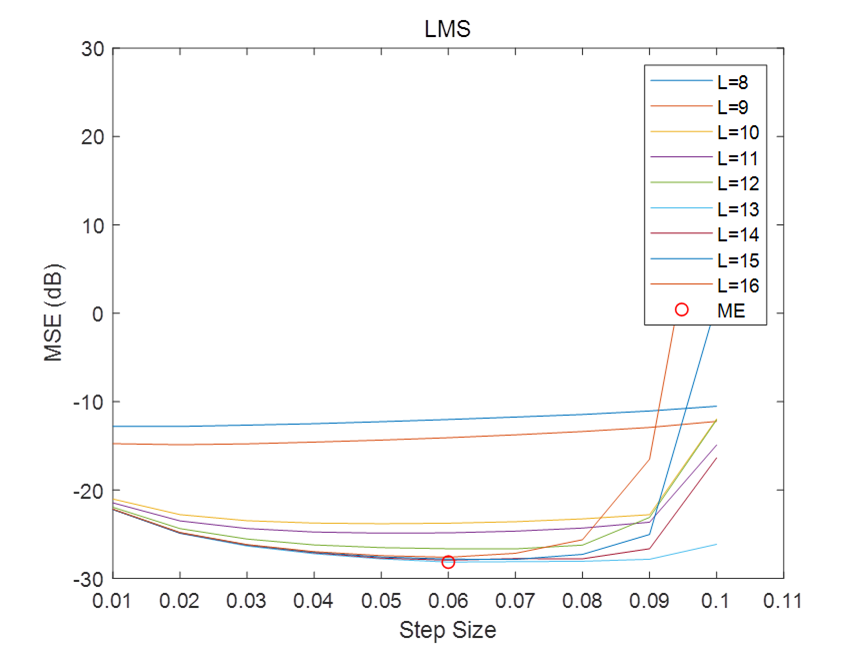
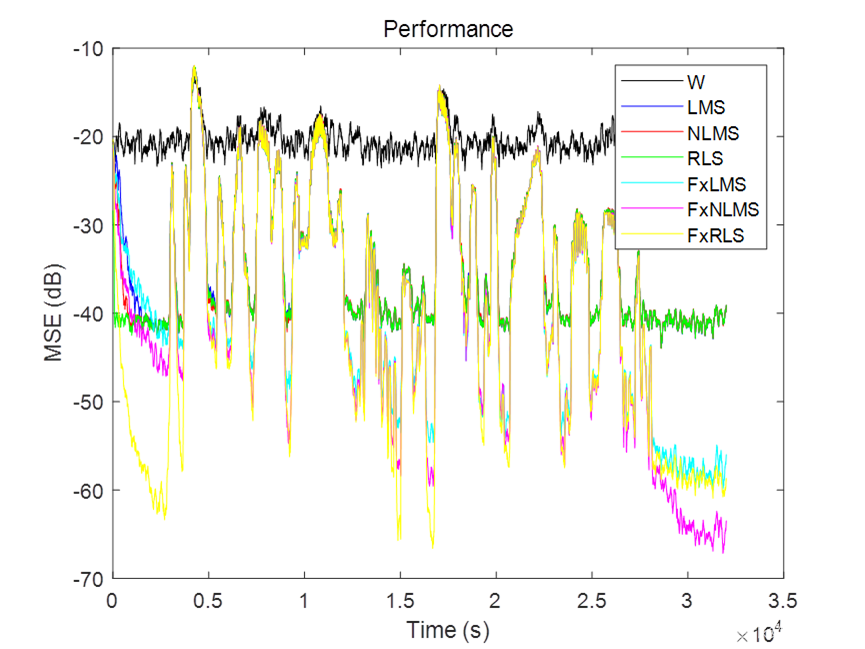
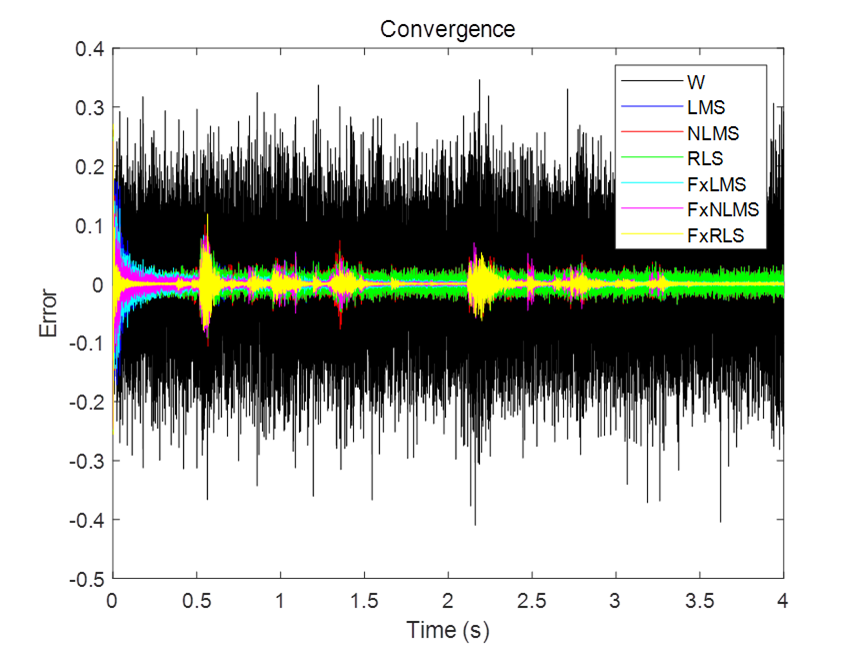
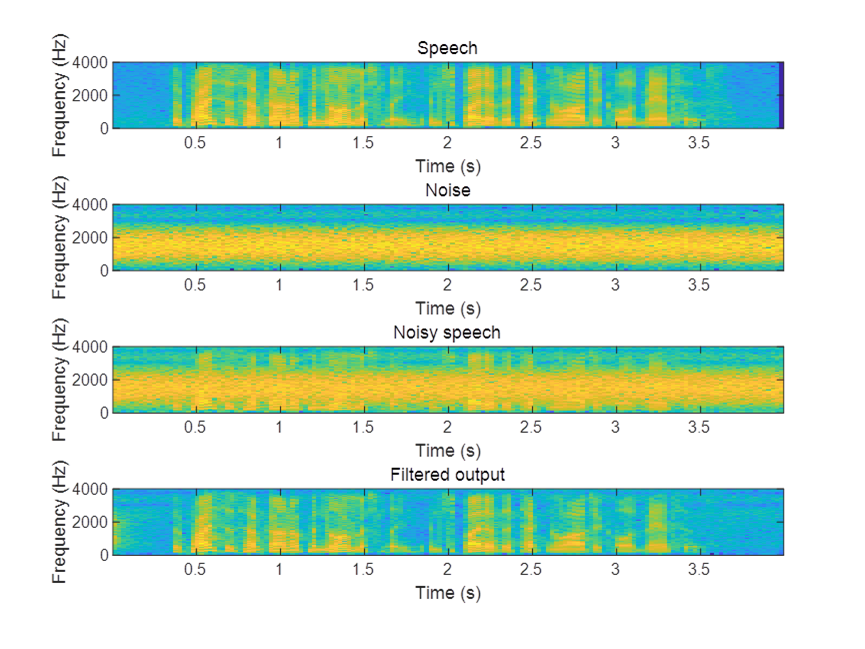
工学博士,担任《Mechanical System and Signal Processing》审稿专家,担任
《中国电机工程学报》优秀审稿专家,《控制与决策》,《系统工程与电子技术》,《电力系统保护与控制》,《宇航学报》等EI期刊审稿专家。
擅长领域:现代信号处理,机器学习,深度学习,数字孪生,时间序列分析,设备缺陷检测、设备异常检测、设备智能故障诊断与健康管理PHM等。



)




】基于BarTender将btw文件转换为zpl文件)
)


)
)





