在C语言中,移位操作符和位操作符是专门针对二进制的数字进行,因此,在描述移位操作符和位操作符之前,我们先来了解十进制,二进制,八进制,十六进制等的含义以及相互之间的转化。
一.进制以及相互的转化
十进制,二进制,八进制,十六进制等只是数值的不同表示形式,十进制就是逢10进1位,二进制就是逢2进1,以此类推。
十进制每个位置上的值的范围是0-9,二进制是0-1,那么他们是如何进行转化的呢?
1.二进制转化为十进制
首先来看,我们是怎么读出十进制的数字的,实际上,例如:123,我们是运用了
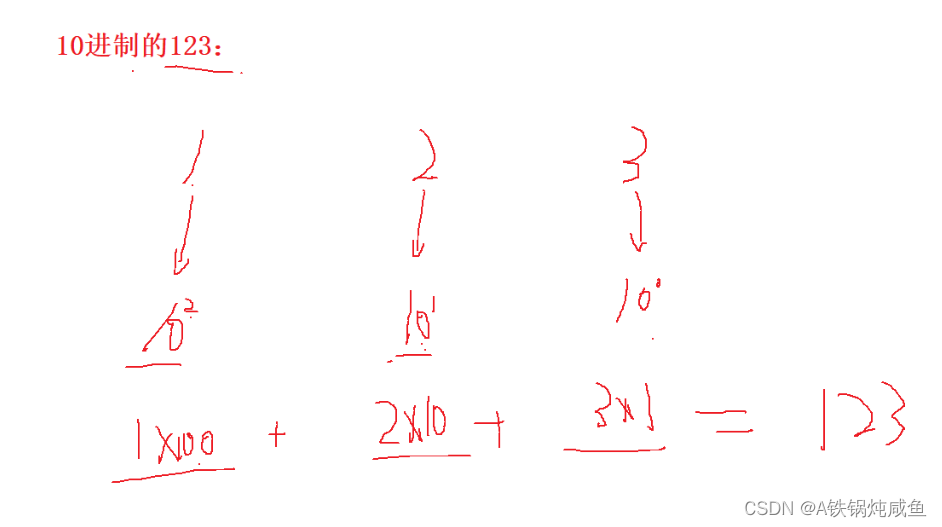
这样的计算方法来获得答案的,3对应的是10的0次方,2×10的一次方,以此类推,最后求和即可
那么我们想把二进制数字转换为十进制的数字,实际上也可以运用这样的计算方法,只不过是改成成了✖2的多少次方。
例如,我们求二进制数字1101转换为十进制的数字:
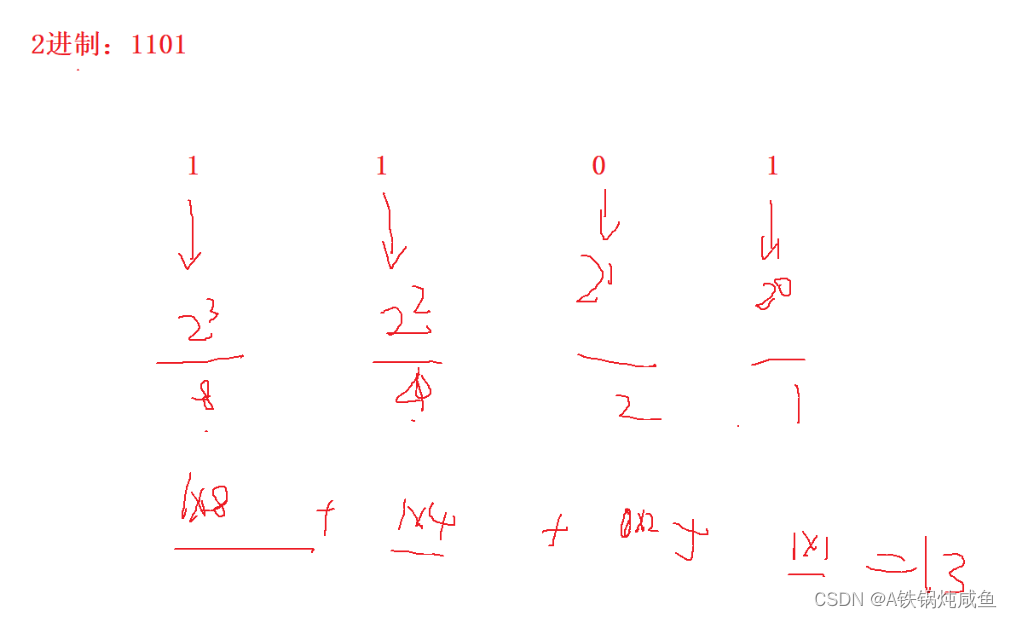
如果我们想将一个八进制数字转换为十进制数字,也是非常简单的:
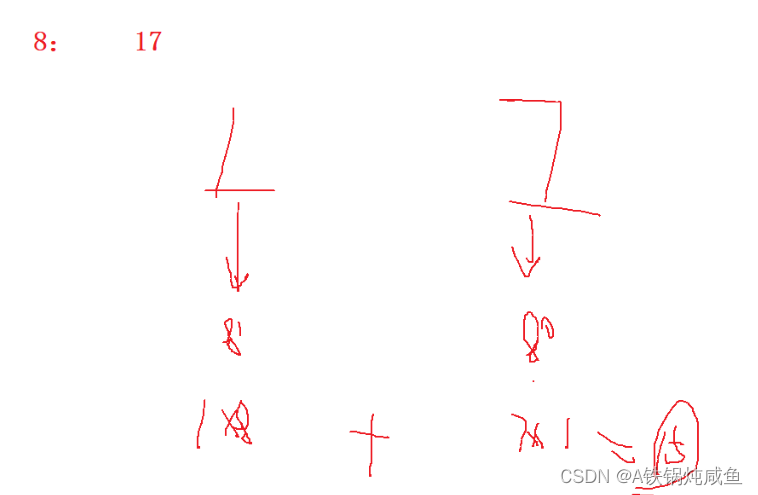
2.十进制转换为二进制
例如,我们要将十进制数字125转换为二进制数字,我们运用这样的方法:
1.将十进制数字除以2,保留整数部分,将余数写在后面
2.一直进行1过程,直到为0
3.余数按反向书写即可获得二进制数字

3.二进制转化为八(十六)进制
从右向左,三个为一组,无法组成一组就单独进行计算,例如二进制数字1011101转换为八进制数字,我们是这样做的:
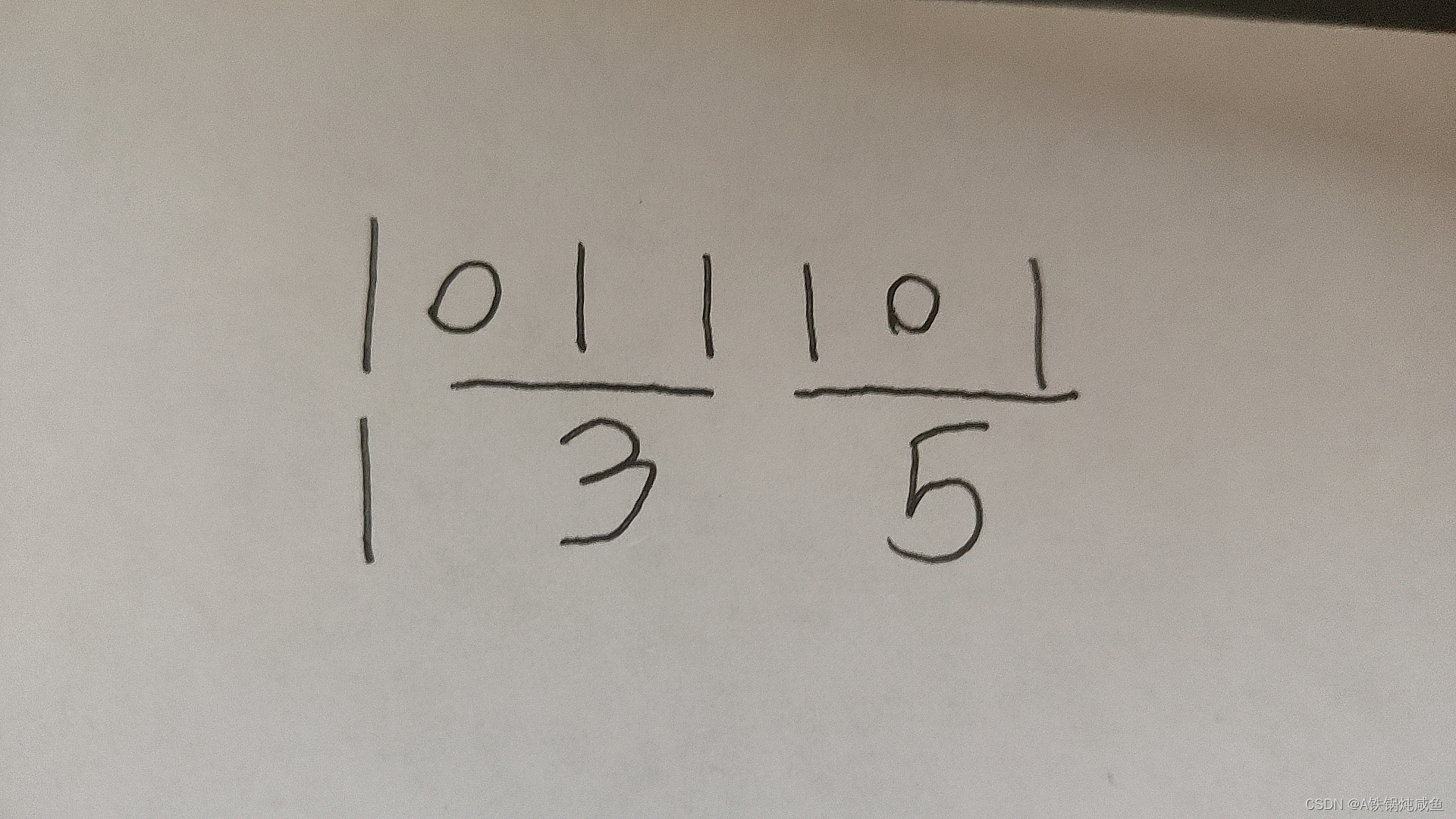
转化为十六进制的时候,从右向左,四个为一组即可
需要注意,十六进制每个位置的范围是0~F,包括0~9,A~F,A是10,F是15
确定八进制的数字时候前面加0,例如023,就是八进制的数字,十六进制前面加0x或0X,十六进制的符号大小写与x的相同
5.八(十六)进制转化为二进制
只需要二进制转化的反向进行转化即可
二.原码,反码,补码
三者描绘的都是整数
由于int类型是4个字节,32个bit,每个bit位置可以存放1个二进制数字,但是只有31位可以放大小,最开头的一位放入的数字表示正负
原码:整数的二进制表示,其中我们知道数字分为正数和负数,因此,我们需要额外来表示正负,如果数字为正数的时候,原码的符号位位0,负数则符号位为1
反码,补码:正数的反码和补码与原码一样
负数的反码:负数的原码除了符号位所有位置取反,如果原位置是1,现在改为0
负数的补码:负数的反码+1
转化过程如图: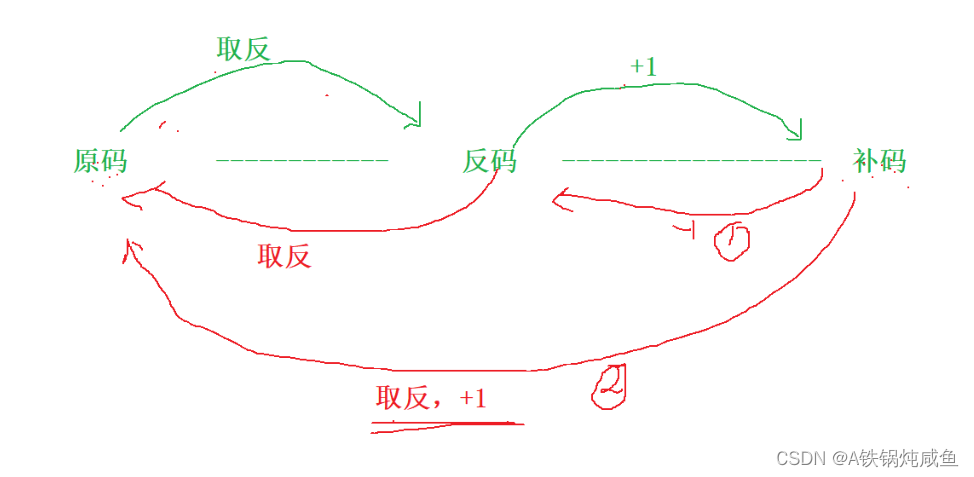
事实上,原码可以经过取反+1变为补码,补码也可以通过取反+1变为原码
我们在运算的时候,统一使用的都是补码来进行运算
三.移位操作符
移位操作符分为:<<左移操作符 >>右移操作符
书写方法是 a >> (移位的数量),例如:
int b = a >> 2;1.左移操作符的移动规律:
采用二进制数字全部左移,空位补0的方法,例如,我们写出10的补码以
![]()
现在向左移位,空位补0,超出范围的去掉
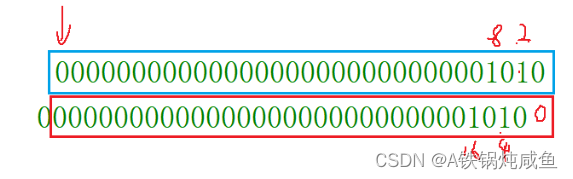
我们会发现,最后得到的结果是20,因为向左移动,代表着*2
负数也是如此,不过记得,移动的是补码,移动后也是补码
2.右移操作符的移动规律
一般来说,采用数字移动的规律,就是全部右移,然后空位补符号位的数字
四.位操作符
位操作符分为:

1.按位与&:
两个数字的补码的二进制数字在某一个位置上都为1时才为1,只要有0则位0,例如:
int a = 4; //00000000000000000000000000000100 4补码
int b = -7; //11111111111111111111111111111001 -7补码//00000000000000000000000000000000我们发现,此时没有相同的,故a&b = 0
2.按位或|:
对应位置有1就是1,都0才是0,例如
int a = 4; //00000000000000000000000000000100 4补码
int b = -7; //11111111111111111111111111111001 -7补码//11111111111111111111111111111101 a|b的补码 //10000000000000000000000000000011 还原为原码//-3一定要记得获得的是补码哦
3.按位异或^:
相同为0,想异为1
int a = 4; //00000000000000000000000000000100 4补码
int b = -7; //11111111111111111111111111111001 -7补码//11111111111111111111111111111101//-34.按位取反~:
所有位置变为与原本不同的数
五.例题
1.不创建(临时)第三个变量,实现整数交换
我们在实现整数交换时,运用的是这种方法:
int main() {int a = 3;int b = 5;int c = 0;c = a;a = b;b = c;printf("%d %d", a, b);return 0;
}
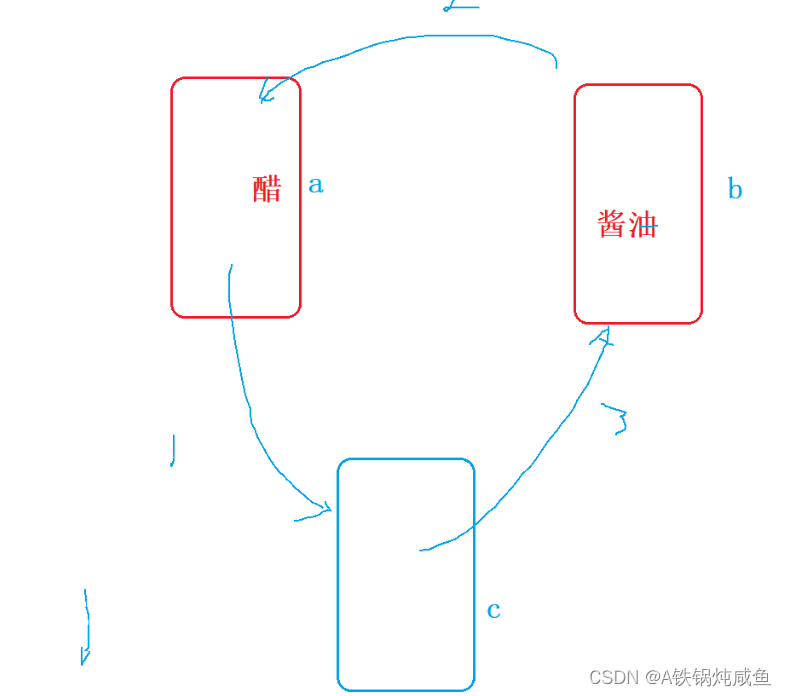 假设有两个瓶子,分别装了醋和酱油,现在让两个瓶子里面的东西反过来,我们额外拿来了一个瓶子,然后进行了操作。
假设有两个瓶子,分别装了醋和酱油,现在让两个瓶子里面的东西反过来,我们额外拿来了一个瓶子,然后进行了操作。
但在这个题目中,他让我们不创建临时变量,也就是不能额外拿来一个瓶子,实现整数的交换
我们可以采用这种方法:
int main() {int a = 3;int b = 5;//当a与b特别大的时候,超过最大值出现位数丢失(溢出)a = a + b; //a = 8 b = 5b = a - b; //b = 3 a = 8a = a - b; //a = 5 a = 3printf("%d %d", a, b);return 0;
}这样就可以交换a与b的值了,但是如果a与b两个整数非常大的时候,我们想加可能超过最大的范围,因此,这个方法有一定的局限性
我们在之前学习了^,它有如下的式子 a ^
a = 0,因为两者完全相同,同时 a ^ 0 = a,我们可以写出如下的代码:
int main() {int a = 3;int b = 5;a = a ^ b;b = a ^ b; // a ^ b ^ b = aa = a ^ b; // a ^ b ^ a = bprintf("%d %d", a, b);return 0;
}在这里,我们将a ^ b 视为了一个整体,进行的运算
2.计算一个数字的二进制数的1的数量
如果一个数字%2等于1,此时它的二进制数字的最后一位为1,我们可以写出如下的函数:
int count(unsigned int m) {int num = 0;if (m % 2) num++;m /= 2;return num;
}其中m要是unsigned int类型,因为m传进去是一串二进制数,如果是负数还需要单独判断,此时,我们将他们统一视为了正数进行的判断
当然,我们也可以通过移位操作符,来判断每一位上是否为1,写出如下的函数:
int count1(unsigned int m) {int count = 0;int i = 0;for (i = 0; i < 32; i++) {if (((m >> i) & 1) == 1)count++;}return count;
}使得m不断向右移动,来计算
同时,n = n ^ (n-1)的方法可以更快的进行运算,函数如下:
// n = n & (n-1) 让n的二进制中最右边的1消失
// n = 0时,执行几次就是有几个1 有几个1统计几次
int count2(unsigned int m) {int count = 0;while (m) {count++;m = m & (m - 1);}return count;
}
感谢您的观看!
如果您想要进行进一步的训练请移步
C语言进制习题-CSDN博客
)
)








:this的使用方法)
)


:简介与使用指南)

——交通灯控制器的multisim仿真)

)
