目录
1 二叉树小结
1.1 模式一
1.2 模式二
2 236. 二叉树的最近公共祖先
3 124. 二叉树中的最大路径和
菜鸟做题(返校版),语言是 C++
1 二叉树小结
菜鸟碎碎念
通过对二叉树的练习,我对 “递归” 有了一些肤浅的理解。我发现 “递归” 并不就等价于,先从上往下找到叶节点,再从下往上一直处理到根节点。它其实存在着两种模式。
1.1 模式一
- 从上到下处理
- 先处理根节点,后处理左右子树
代码一般都长这样:
function(Treenode * root) {if (!root) return;root->val...function(root->left);function(root->left);...
}比如 437 题中要算前缀和,那么我们自然想到要从上到下进行累加,因此选择模式一。
1.2 模式二
- 从下到上处理
- 先处理左右子树,后处理根节点
代码一般都长这样:
function(Treenode * root) {if (!root) return;function(root->left);function(root->right);root->val......
}比如 236 题要找公共祖先,那么我们自然想到要从下往上找,因此选择模式二。
2 236. 二叉树的最近公共祖先
解题思路:
- 判断当前节点的左右子树是否存在 p 或 q
- 一旦当前节点的左右子树各自包含了 p 或 q
- 那么当前节点为最近公共祖先
详细代码:
① 判断左右子树中是否存在 p 或 q,若有则 lson、rson 会为 true:
bool lson = helper(root->left, p, q);
bool rson = helper(root->right, p, q);相应的返回值如下:
return lson || rson || (root == p || root == q);意思是,对于某个子树的根节点,如果它的左右子树包含 p 或 q,或者它本身就是 p 或 q,那么等价于这个子树包含 p 或 q 。比如:对于浅绿色子树,根节点 “5” 的右子树(深绿色)包含 q,那么也等价于浅绿色子树包含 q 。
![]()
② 判断当前节点是否为最近公共祖先:
if ((lson && rson) || ((root == p || root == q) && (lson || rson))) {ans = root;
} 这一行代码非常 tricky,((root == p || root == q) && (lson || rson)) 是啥意思?它的意思是,root 等于 p 或者 q,左子树或右子树找到 p 或者 q,只要这两个条件同时成立,那么当前节点 root 就是最近公共祖先。
为什么这个判断条件没有要求指明 root 和 lson、rson 分别找到的是 p 还是 q 呢?因为只要一方确定了,另一方自然就确定了。比如:如果 root 等于 p,那么 lson 或者 rson 之前找到的一定是 q 而不是 p,否则就矛盾了。
class Solution {
public:TreeNode * ans;bool helper(TreeNode* root, TreeNode* p, TreeNode* q) {if (!root) return false;bool lson = helper(root->left, p, q);bool rson = helper(root->right, p, q);if ((lson && rson) || ((root == p || root == q) && (lson || rson))) {ans = root;} return lson || rson || (root == p || root == q);}TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {helper(root, p, q);return ans;}
};3 124. 二叉树中的最大路径和
解题思路:
- 从下向上遍历二叉树
- 路径和 = 根节点 + 根节点的左子树 + 根节点的右子树
- 根节点向父节点推荐自己
这里说的根节点泛指每个子树的根节点;“根节点的左子树” 具体是指从左子树中找出的最大路径和,后文所提到的 “左子树” 也是这个意思。
思路说明图:
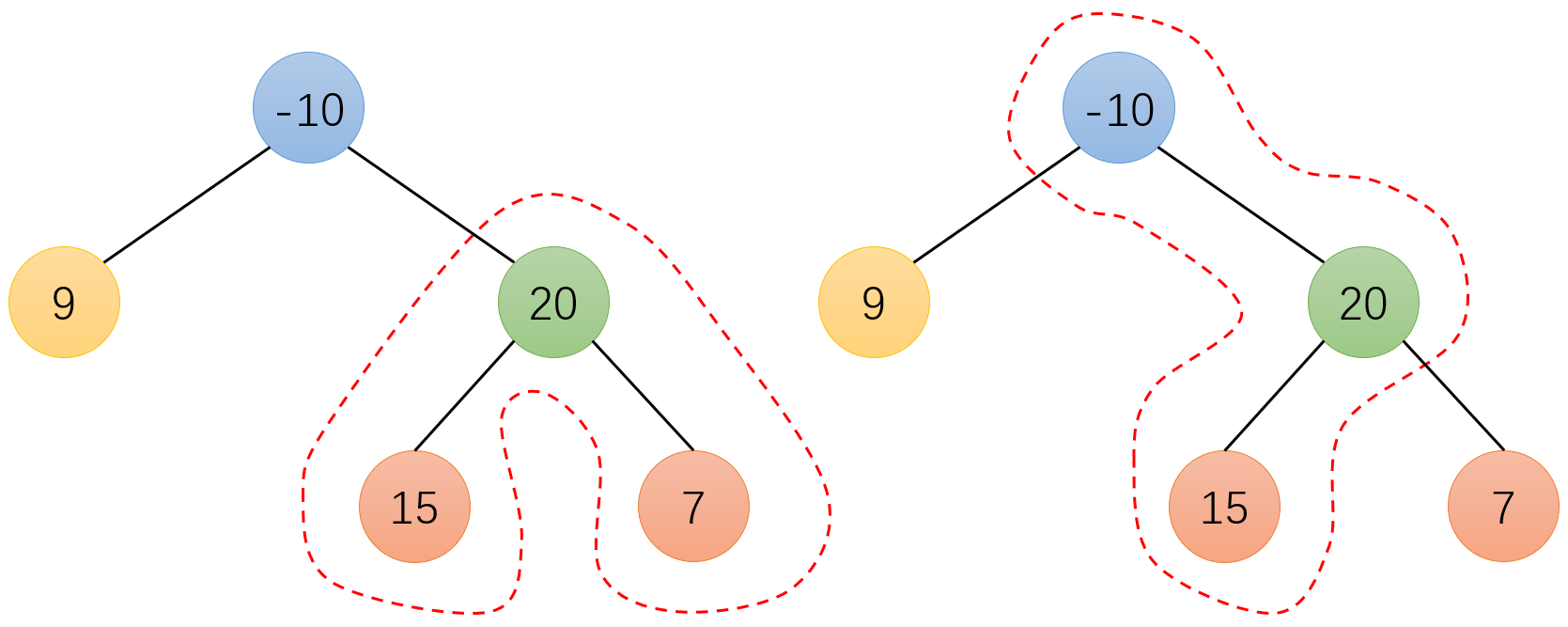
针对根节点 “20”,“20” 的左子树(“15”)和右子树(“7”)会向 “20” 自荐,只要它们不拖后腿(路径和为负),那么 “20” + 它的左子树 + 它的右子树 的路径和就是最大的。接着,“20” 会选择左子树和右子树中的较大者,一起向父节点 “-10” 自荐。以此类推。
为什么 “20” 只能携带一棵子树?因为我们构造的是一条笔直的路径,如果左右子树都带上,那这条路就分叉了。
class Solution {
public:int maxSum = INT_MIN;int helper(TreeNode* root) {if (!root) return 0;// 获取左右子树中的最大路径和int leftSum = max(0, helper(root->left));int rightSum = max(0, helper(root->right));// 计算当前子树的最大路径和int pathSum = root->val + leftSum + rightSum;maxSum = max(maxSum, pathSum);// 向父节点自荐return root->val + max(leftSum, rightSum);}int maxPathSum(TreeNode* root) {helper(root);return maxSum;}
};)






)

)





23-191)
---页面元素定位器)


