【Leetcode】889. 根据前序和后序遍历构造二叉树

文章目录

题目
思路
代码
结果

题目

题目链接
给定两个整数数组，preorder 和 postorder ，其中 preorder 是一个具有无重复值的二叉树的前序遍历，postorder 是同一棵树的后序遍历，重构并返回二叉树。
如果存在多个答案，您可以返回其中任何一个。

示例 1：

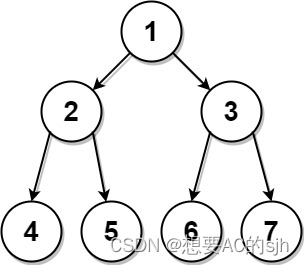
输入：preorder = [1,2,4,5,3,6,7], postorder = [4,5,2,6,7,3,1]
输出：[1,2,3,4,5,6,7]

示例 2:
输入: preorder = [1], postorder = [1]
输出: [1]

提示：

1 <= preorder.length <= 30
1 <= preorder[i] <= preorder.length
preorder 中所有值都不同
postorder.length == preorder.length
1 <= postorder[i] <= postorder.length
postorder 中所有值都不同
保证 preorder 和 postorder 是同一棵二叉树的前序遍历和后序遍历

思路

考虑到二叉树的前序遍历与后序遍历的特性，我们知道前序遍历的第一个元素 preorder[0] 与后序遍历的最后一个元素 postorder[n-1] 都对应着二叉树的根节点。获取了根节点后，我们需要将根节点的左子树和右子树区分开来，这里有两种情况需要考虑：

若原二叉树的根节点的左子树不为空，则 preorder[1] 对应着左子树的根节点；
若原二叉树的根节点的左子树为空，则 preorder[1] 对应着右子树的根节点。

对于上述两种情况，我们无法直接区分出 preorder[1] 到底是哪一种情况。但对于第二种情况，我们可以将原二叉树的右子树移到左子树，这样得到的二叉树的前序遍历数组与后序遍历数组与原二叉树相同。因为二叉树的节点值互不相同，所以我们可以在后序遍历数组中找到一个位置 k，使得 postorder[k] = preorder[1]，这样左子树的节点数目为 k+1。基于此思路，我们可以对前序遍历数组和后序遍历数组进行分治处理，将前序遍历数组划分为根节点、左子树节点和右子树节点三个部分，后序遍历数组也划分为左子树节点、右子树节点和根节点三个部分。因此，问题被划分为：

根据左子树节点的前序遍历与后序遍历数组构造二叉树；
根据右子树节点的前序遍历与后序遍历数组构造二叉树。

当节点数目为 1 时，对应构造的二叉树只有一个节点。我们可以递归地对问题进行求解，从而得到构造的二叉树。

代码

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/class Solution {
public:TreeNode* constructFromPrePost(vector<int>& preorder, vector<int>& postorder) {int n = preorder.size();unordered_map<int, int> postMap;for (int i = 0; i < n; i++) {postMap[postorder[i]] = i;}return dfs(preorder, postorder, postMap, 0, n - 1, 0, n - 1);}TreeNode* dfs(vector<int>& preorder, vector<int>& postorder, unordered_map<int, int>& postMap, int preLeft, int preRight, int postLeft, int postRight) {if (preLeft > preRight) {return nullptr;}int leftCount = 0;if (preLeft < preRight) {leftCount = postMap[preorder[preLeft + 1]] - postLeft + 1;}return new TreeNode(preorder[preLeft],dfs(preorder, postorder, postMap, preLeft + 1, preLeft + leftCount, postLeft, postLeft + leftCount - 1),dfs(preorder, postorder, postMap, preLeft + leftCount + 1, preRight, postLeft + leftCount, postRight - 1));}
};