1. 二叉树的最近公共祖先
236. 二叉树的最近公共祖先![]() https://leetcode.cn/problems/lowest-common-ancestor-of-a-binary-tree/
https://leetcode.cn/problems/lowest-common-ancestor-of-a-binary-tree/
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
示例 1:
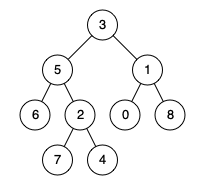
输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出:3
解释:节点 5 和节点 1 的最近公共祖先是节点 3 。示例 2:

输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出:5
解释:节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。解题思路
找祖先,涉及到回溯,所以要使用中序递归。
考虑递归的三要素:
- 参数:当前节点root,q和p两个要找的节点
- 返回值:boolean,当子树包含q的时候返回True,否则返回false
- 终止条件:root为null的时候,返回false
- 递归逻辑:无法提前终止,当左右都返回True的时候,可以确定祖先,但是,祖先的上一层无法判断是只有一个还是两个了。所以需要一个TreeNode来保存祖先。
代码
class Solution {TreeNode ancestor = null;public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {findAncestor(root, p, q);return ancestor;}public boolean findAncestor(TreeNode root, TreeNode p, TreeNode q) {if (root == null)return false;boolean cur = root == p || root == q;boolean left = findAncestor(root.left, p, q);boolean right = findAncestor(root.right, p, q);int count = 0;if (cur)count++;if (left)count++;if (right)count++;if (count == 2)ancestor = root;return left || right || cur;}
}2. 二叉搜索树的最近公共祖先
235. 二叉搜索树的最近公共祖先![]() https://leetcode.cn/problems/lowest-common-ancestor-of-a-binary-search-tree/
https://leetcode.cn/problems/lowest-common-ancestor-of-a-binary-search-tree/
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
例如,给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]
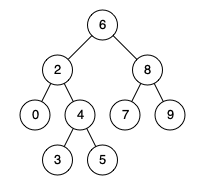
示例 1:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6
解释: 节点 2 和节点 8 的最近公共祖先是 6。示例 2:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。解题思路
二叉搜索树肯定比普通的二叉树有优化的地方,二叉搜索树的公共祖先一定是位于p和q的中间的,并且只有一个这样的祖先,因为再网上就又变成了位于两边了。
- 参数:root,p,q
- 返回值:返回找到的位于中间的节点
- 终止条件:位于中间的时候,返回root
- 递归逻辑:小于min的时候走右侧,大于max的时候走左侧
class Solution {public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {if (root.val > Math.max(p.val, q.val))return lowestCommonAncestor(root.left, p, q);else if (root.val < Math.min(p.val, q.val))return lowestCommonAncestor(root.right, p, q);elsereturn root;}
}


标签 隐藏百分比(%) ,反向显示 ,自定义颜色, demo 复制粘贴拿去用)
)
![[Mac软件]Mac上的最佳3D建模工具-犀牛Rhinoceros 8 for Mac v8.4.24044.1500完美兼容激活](http://pic.xiahunao.cn/[Mac软件]Mac上的最佳3D建模工具-犀牛Rhinoceros 8 for Mac v8.4.24044.1500完美兼容激活)



)
)

)





-dockerfile制作镜像)
