在vscode中配置好leetcode之后，一般最常用的就是通过cookie登录leetcode ;

首先点击sign in ， 然后选择最下面的 ， LeetCode Cookie !

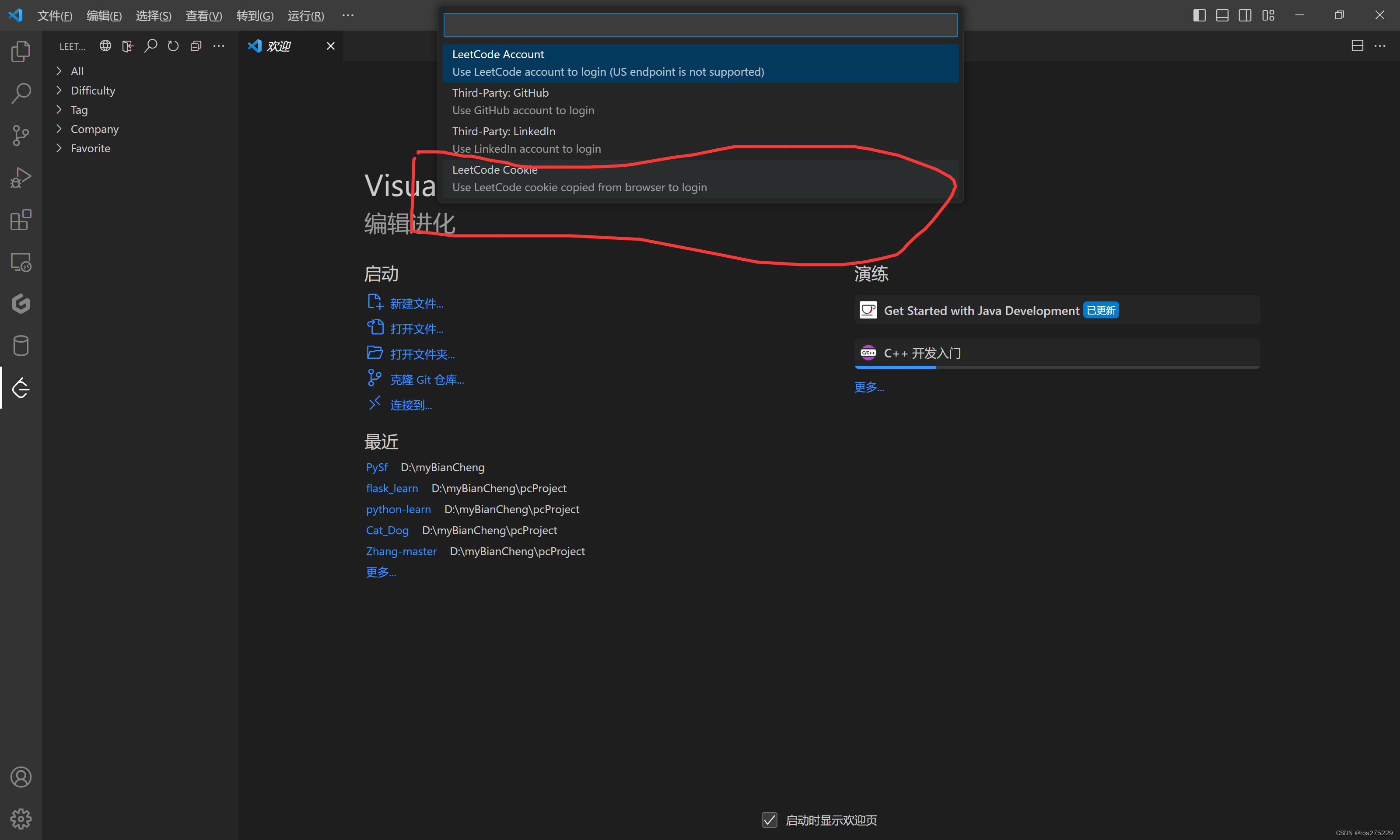
 然后输入username(也就是你的lc用户名) 或者 你leetcode绑定的邮箱 ;

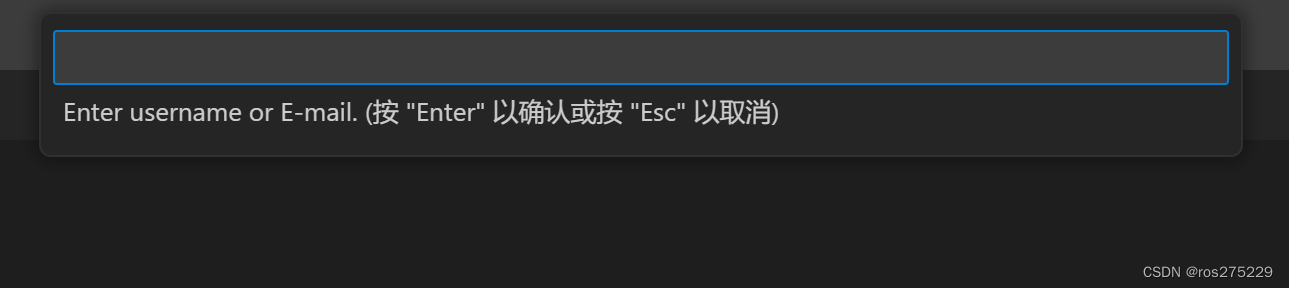
输入完成之后 ;

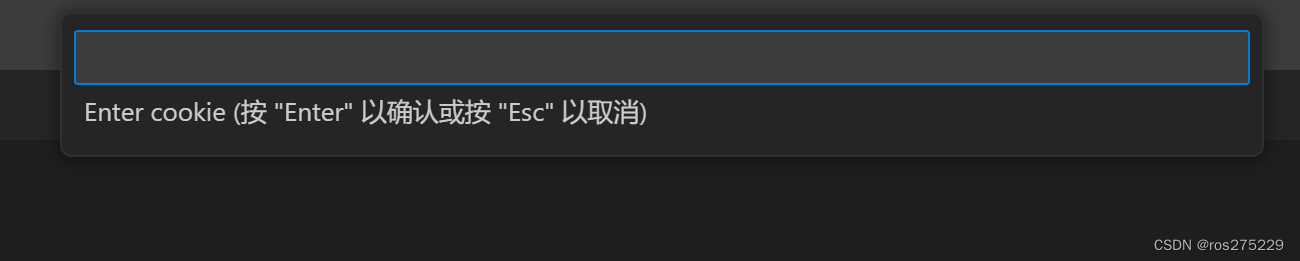
就是要你输入你的leetcode的Cookie;

首先打开你的主页 ， 右键点击检查;

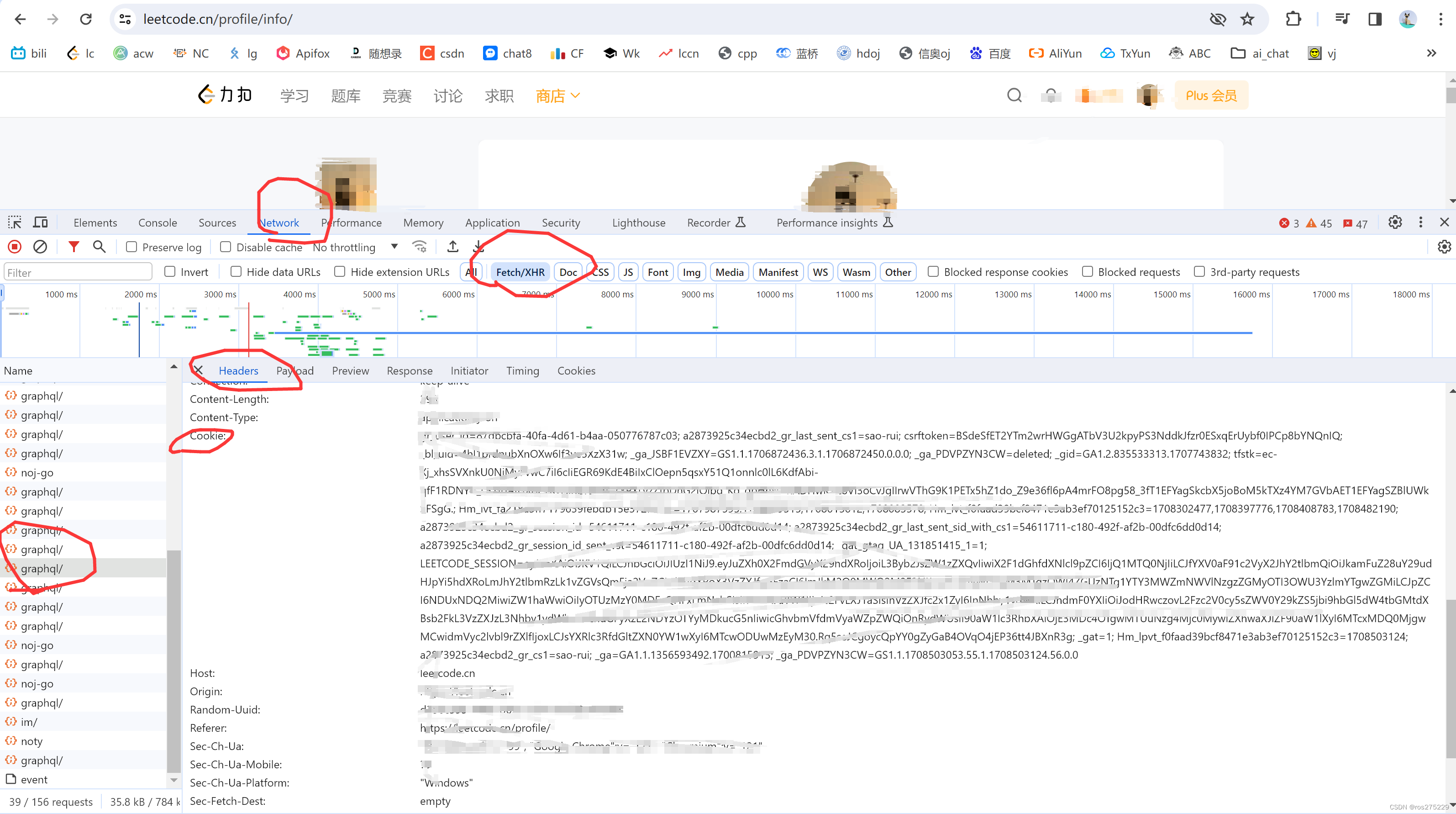
然后随便点一个地方，按照上图将cookie复制进入vscode输入就行了 ;

然后就可以快乐的用vscode刷leetcode上的题了 ;