数据结构与算法：栈

朋友们大家好啊，在链表的讲解过后，我们本节内容来介绍一个特殊的线性表：栈，在讲解后也会以例题来加深对本节内容的理解

栈

栈的介绍
- 栈进出栈的变化形式
栈的顺序存储结构的有关操作
- 栈的结构定义与初始化
- 压栈操作
- 出栈操作
- 获取栈顶元素和有效元素个数
- 判断是否为空和栈的销毁
栈的链式存储结构的有关操作
- 链表的创建
- 链式栈的定义
- 初始化
- 压栈和出栈
- 检查栈是否为空
栈的应用--有效的扩号

栈的介绍

在应用软件中，栈的应用非常普遍，比如使用浏览器上网时，会有一个后退键，点击后可以按访问顺序的逆序加载浏览过的网页
在这里插入图片描述
很多类似的软件，比如word等文档或编辑软件都有撤销的操作，也是用栈的方式来实现的

栈是一种特殊的线性数据结构，仅支持在一个位置进行添加元素（称为“入栈”或“push”操作）和移除元素（称为“出栈”或“pop”操作）的操作。这个位置就是栈顶（Top）。由于栈是后进先出（LIFO, Last In First Out）的数据结构，最后一个添加到栈中的元素将是第一个被移除。

栈是限定仅在表尾进行插入和删除操作的线性表

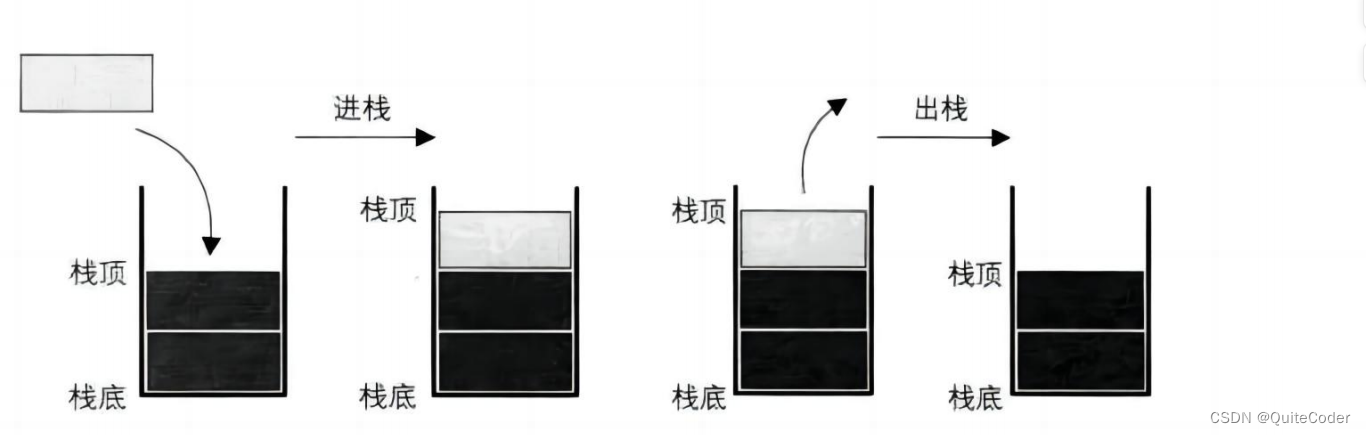
在这里插入图片描述
栈首先是一个线性表，说明栈元素具有线性关系，在定义中说在线性表的表尾进行插入和删除操作，这里的表尾是指栈顶

它的特殊之处就在于它的删除和插入始终只能在栈顶进行

栈进出栈的变化形式

首先提一个问题，最先进栈的元素，是不是一定最后出栈呢？
答案是不一定的，在不是所有元素都进栈的情况下，先进去的元素也可以出栈，保证是栈顶元素出栈就可以

举例，如果我们有1、2、3三个数字一次进栈，会有哪些出栈次序呢？

第一种：1、2、3进，再3、2、1出，出栈次序为321
第二种：1进，1出，2进，2出，3进，3出。进一个出一个，出栈次序为123
第三种，1进，2进，2出，1出，3进，3出，出栈顺序为213
第四种：1进，1出，2进，3进，3出，2出，出栈顺序为132
第五种：1进，2进，2出，3进，3出，1出，出栈次序为231

栈的顺序存储结构的有关操作

对于栈来讲，线性表的操作特性它都具备，由于它的特殊性，特别是插入和删除操作，我们改名为push和pop

线性表是用数组来实现的，对于栈这一种只能一头插入的线性表来说，下表为0的一段作为栈底

栈的结构定义与初始化

typedef int STDataType;typedef struct Stack
{STDataType* a;int top;int capacity;
}ST;

对栈进行初始化，构造initial函数

void StackInit(ST* ps)
{assert(ps);ps->a = NULL;ps->top = -1;ps->capacity = 0;}

首先assert断言ps是否为空指针，将a指向NULL，capacity置为0，而top置为-1

在栈的实现中，top变量一般用来指示栈顶元素的位置。对于一个空栈来说，不存在任何元素，因此没有一个合理的位置可以被称为栈顶。在这种情况下，需要一个特殊的值来表示栈是空的
在进行入栈和出栈操作时，top的更新逻辑变得简单直接。例如，每当添加一个新元素到栈中时，先将top加1（这将把top从-1改为0，表示第一个元素的位置），然后在top对应的位置上存放新元素

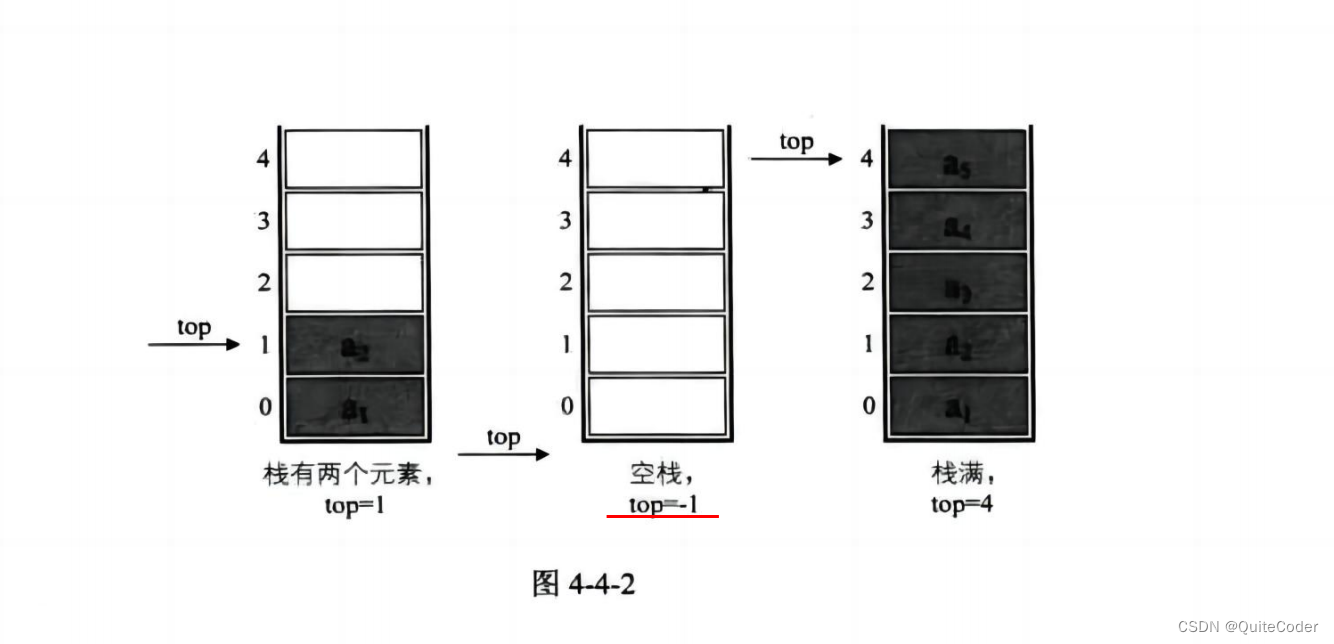
在这里插入图片描述
保证top指向栈顶元素

压栈操作

void StackPush(ST* ps, STDataType x) {assert(ps != NULL); // 检查栈是否已满if (ps->top + 1 == ps->capacity) {int newcapacity=ps->capacity==0?4:ps->capacity*2; STDataType* tmp = (STDataType*)realloc(ps->a, sizeof(STDataType) * newcapacity);if (tmp == NULL) {perror("realloc fail");return;}ps->a = tmp;ps->capacity = newcapacity;}// 先将栈顶索引top增加1，然后在新的栈顶位置存入元素xps->top++;ps->a[ps->top] = x;
}

首先检查栈是否已满，即：if (ps->top + 1 == ps->capacity)。这是通过比较top + 1（即如果添加新元素后的栈顶索引）和capacity（栈的容量）来实现的。
如果栈满，执行扩容操作。新的容量newcapacity为当前容量的两倍，但如果当前容量为0，则初始化容量为4。
使用realloc尝试扩容
栈顶索引top增加1，以便于在正确的位置添加新元素。
在新的栈顶位置存入元素x，即ps->a[ps->top] = x;

出栈操作

void StackPop(ST* ps) {assert(ps != NULL); if (ps->top == -1) { printf("栈已空，无法执行出栈操作。\n");return;}ps->top -= 1; 
}

两个操作没有涉及任何循环，时间复杂度均为O(1);

获取栈顶元素和有效元素个数

STDataType StackTop(ST* ps) {assert(ps != NULL);if (ps->top == -1) {printf("错误：试图从空栈中获取元素。\n");exit(EXIT_FAILURE); }return ps->a[ps->top];
}

int StackSize(ST* ps) {assert(ps != NULL); return ps->top + 1; 
}

判断是否为空和栈的销毁

bool StackEmpty(ST* ps) {assert(ps != NULL); return ps->top == -1; 
}

在C语言中，当一个函数的返回类型被声明为bool（需要包含<stdbool.h>头文件），那么它只能返回两个值之一：true或false。

true通常被定义为整数1。
false被定义为整数0。
这意味着，当你看到一个函数的返回类型是bool，你可以期望该函数根据其执行的操作或检查的条件，返回表示“真”或者“假”的结果。这样的函数通常用于进行某种条件检测或确认某事是否成立。

这行代码核心地检查栈是否为空。在这里，ps->top是栈顶元素的索引。通常情况下，当栈为空时，栈顶索引top被设置为-1来表示栈内没有元素。如果ps->top等于-1，函数返回true，表示栈为空；否则返回false，表示栈中有元素。

void StackDestroy(ST* ps) {assert(ps != NULL); // 确保栈指针ps非空free(ps->a);        // 释放动态数组ps->a = NULL;       // 将指针设为NULL，防止悬挂指针ps->top = -1;       // 重置栈顶指标ps->capacity = 0;   // 重置栈容量
}

栈的链式存储结构的有关操作

讲完了栈的顺序存储，我们接着来看栈的链式存储

思考一下，栈只在栈顶进行删除和插入，那么栈顶是放在链表的头端还是尾端呢？

当使用链表实现链式栈时，通常选择链表的头部作为栈顶，因为这种方法更高效、实现也更简单：

在链表头部插入或删除节点只需要O(1)的时间复杂度，因为这些操作不需要遍历整个链表。这对于栈操作（即push和pop操作）非常理想，因为它们也应该是O(1)的时间复杂度
链表有头指针，栈有顶部指针，可以做到合二为一

链表的创建

typedef int STDataType;typedef struct StackNode {STDataType data;                     struct StackNode* next;       
} StackNode;

链式栈的定义

typedef struct LinkedStack{StackNode* top;               int size;                     
} LinkedStack;

初始化

初始化一个空栈，只需要将栈顶指针设置为NULL，栈的大小设置为0

void Initialize(LinkedStack* stack) {stack->top = NULL;stack->size = 0;
}

压栈和出栈

void Push(LinkedStack* stack, STDataType x) {StackNode* newNode = (StackNode*)malloc(sizeof(StackNode));if (newNode == NULL) {printf("Memory allocation failed\n");return;}newNode->data = x ;newNode->next = stack->top;    // 新节点的下一个节点就是当前的栈顶stack->top = newNode;          // 更新栈顶为新节点stack->size++;
}

推入新元素需要创建一个新的节点，并将其插入到链表的头部。

int Pop(LinkedStack* stack) {if (stack->top == NULL) {      // 检查栈是否为空printf("Stack is empty\n");return -1;                 // 使用-1表示错误情况，实际使用中应考虑其他错误处理方式}StackNode* temp = stack->top;  // 临时保存栈顶节点int data = temp->data;         // 获取栈顶数据stack->top = temp->next;       // 更新栈顶指针为下一个节点free(temp);                    // 释放原栈顶节点的内存stack->size--;return data;                   // 返回栈顶数据
}

弹出栈顶元素先要检查栈是否为空。如果不为空，将栈顶节点从链表中移除，并释放它所占用的内存。

检查栈是否为空

检查链式栈是否为空也很简单，只需检查栈顶指针是否为NULL。

int IsEmpty(LinkedStack* stack) {return stack->top == NULL;
}

栈的应用–有效的扩号

给定一个只包括 ‘(’，‘)’，‘{’，‘}’，‘[’，‘]’ 的字符串 s ，判断字符串是否有效。

有效字符串需满足：

左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。
每个右括号都有一个对应的相同类型的左括号。

这个问题可以通过使用栈来轻松解决。基本思想是遍历字符串中的每个字符，对于每个开放括号（(, {, [），我们将其推入栈中。对于每个关闭括号（), }, ]），我们检查它是否与栈顶的开放括号匹配。如果匹配，则弹出栈顶元素并继续处理字符串的下一个字符。如果在任何时候遇到不匹配的情况，或者在遍历完字符串后栈不为空，则字符串不是有效的

typedef char STDataType;typedef struct Stack
{STDataType* a;int top;int capacity;
}ST; void StackInit(ST* ps)
{assert(ps);ps->a = NULL;ps->top = -1;ps->capacity = 0;}void StackPush(ST* ps, STDataType x) {assert(ps != NULL); if (ps->top + 1 == ps->capacity) {int newcapacity=ps->capacity==0?4:ps->capacity*2;STDataType* tmp = (STDataType*)realloc(ps->a, sizeof(STDataType) * newcapacity);if (tmp == NULL) {perror("realloc fail");return;}ps->a = tmp;ps->capacity = newcapacity;}ps->top += 1;ps->a[ps->top] = x;
}
void StackPop(ST* ps) {assert(ps != NULL); if (ps->top == -1) {printf("栈已空，无法执行出栈操作。\n");return;}ps->top -= 1; 
}
STDataType StackTop(ST* ps) {assert(ps != NULL); if (ps->top == -1) {printf("错误：试图从空栈中获取元素。\n");exit(EXIT_FAILURE); }return ps->a[ps->top];
}
int StackSize(ST* ps) {assert(ps != NULL); return ps->top + 1; 
}
bool StackEmpty(ST* ps) {assert(ps != NULL); return ps->top == -1; 
}
void StackDestroy(ST* ps) {assert(ps != NULL); free(ps->a);        ps->a = NULL;       ps->top = -1;       ps->capacity = 0;  
}

我们首先列出准备好的函数，这里的数据类型为字符类型，只需要将typedef int STDataType;改为typedef char STDataType;

bool isValid(char* s) 
{ST sa;StackInit(&sa);while(*s){if(*s=='['||*s=='{'||*s=='('){StackPush(&sa,*s);}else{if(StackEmpty(&sa))return false;char top=StackTop(&sa);StackPop(&sa);if(*s==']'&& top!='['||*s=='}'&&top!='{'||*s==')'&&top!='('){return false;}}++s;}bool ret =StackEmpty(&sa);StackDestroy(&sa);return ret;
}

使用while(*s)循环遍历字符串s中的每个字符。对于每个字符有两种情况：

左括号（[, {, (）：如果字符是左括号之一，使用StackPush(&sa,*s);将其推入栈中。
右括号（], }, )）：如果字符是右括号，首先检查栈是否为空，如果空，则立即返回false，表示没有对应的左括号与当前右括号匹配。如果栈不为空，则获取栈顶元素top=StackTop(&sa);并使用StackPop(&sa);将其从栈中弹出。然后检查栈顶元素是否与当前的右括号匹配，如果不匹配，则返回false。
结束条件：遍历结束后，使用bool ret =StackEmpty(&sa);检查栈是否为空。如果栈为空，意味着所有的左括号都已被正确匹配，返回true；否则，返回false。最后，StackDestroy(&sa);销毁栈以释放可能分配的资源

本节内存到此结束！感谢大家的阅读！