240.编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性：
每行的元素从左到右升序排列。
每列的元素从上到下升序排列。
示例 1：
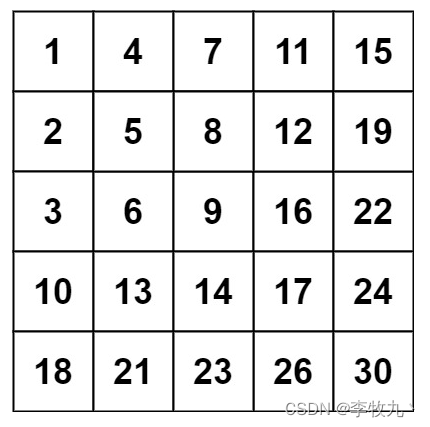
输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
输出：true
示例 2：
输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
输出：false
两个示例为同一矩阵：

• 仔细观察你会发现，如果以右上角为顶点，逆时针旋转 45^o，这就类似于二叉搜索树，左边的数都小于父节点，右边的数都大于右节点，所以我们从顶点 matrix[i,j] 开始搜索，当它小于 target 我们就 i+1 去往右节点，当它大于 target 我们就 j-1 去左顶点

•   public boolean searchMatrix(int[][] matrix, int target) {int row = 0, col = matrix[0].length - 1;while(row < matrix.length && col >= 0){if(matrix[row][col] > target)col--;else if(matrix[row][col] < target)row++;else return true;}return false;}
  

• 说实话，想到有序应该最先想到二分，我们直接遍历每一行进行二分查找，由于矩阵从上到下也是升序，所以在从上到下遍历每一行时，左上角也就是当前遍历行的行首为未查找部分矩阵的最小值，target 小于行首则说明小于剩下的所有值，那直接可以退出循环返回 false 了，而如果 target 大于行尾则直接查下一行即可。

•   public boolean searchMatrix(int[][] matrix, int target) {int n = matrix[0].length - 1;for(int i=0;i<matrix.length;i++){if(matrix[i][0] > target)break;if(matrix[i][n] < target)continue;int col = binarySearch(matrix[i], target);if (col != -1) return true;}return false;}public int binarySearch(int[] nums, int target){int left = 0, right =nums.length - 1;int mid = -1;while(left <= right){mid = left + (right - left) / 2;if(nums[mid] == target)return mid;if(nums[mid] < target) left = mid + 1;else right = mid - 1;}return -1;}