这是树的第19篇算法,力扣链接。
给定一个二叉树:
struct Node {int val;Node *left;Node *right;Node *next; }填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为
NULL。初始状态下,所有 next 指针都被设置为
NULL。示例 1:
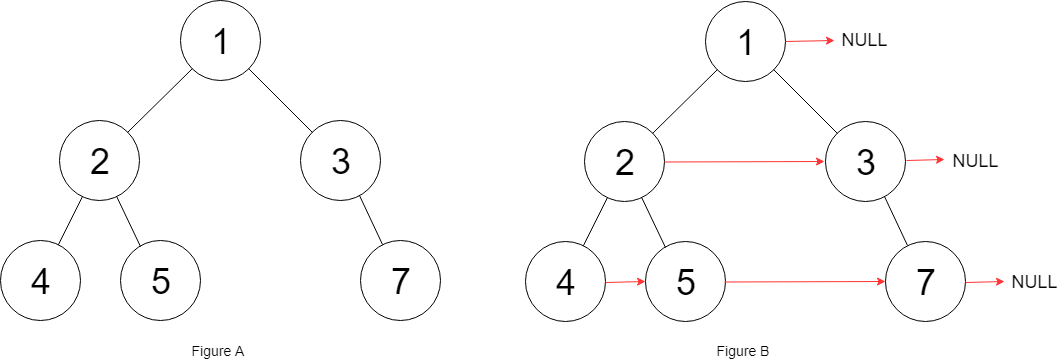
输入:root = [1,2,3,4,5,null,7] 输出:[1,#,2,3,#,4,5,7,#] 解释:给定二叉树如图 A 所示,你的函数应该填充它的每个 next 指针,以指向其下一个右侧节点,如图 B 所示。序列化输出按层序遍历顺序(由 next 指针连接),'#' 表示每层的末尾。
这道题和之前最本质的区别是这棵树不一定是完美二叉树,意味着有几个子叶可能缺失,但是广度/层级遍历不会受到影响。
func connect(root *Node) *Node {if root == nil {return nil}queue := []*Node{root}for len(queue) > 0 {var prev *Nodefor _, node := range queue {if prev != nil {prev.Next = node}if node.Left != nil {queue = append(queue, node.Left)}if node.Right != nil {queue = append(queue, node.Right)}prev = nodequeue = queue[1:]}}return root
}另一个做法之前是保持最左节点在这里可能行不太通了,我们只能一个根节点一个根节点的处理。
func connect(root *Node) *Node {start := rootfor start != nil {var nextStart, prev *Nodelink := func(cur *Node) {if cur == nil {return}if nextStart == nil {nextStart = cur}if prev != nil {prev.Next = cur}prev = cur}for node := start; node != nil; node = node.Next {link(node.Left)link(node.Right)}start = nextStart}return root
}










)




)



