本文主要参考的视频教程如下:
8小时学完线代【中国大学MOOC*小元老师】线性代数速学_哔哩哔哩_bilibili
另外这个视频可以作为补充:
【考研数学 线性代数 基础课】—全集_哔哩哔哩_bilibili
行列式的概念和定义
一般会由方程组来引出行列式
比如一个二阶行列式
二阶行列式的计算就是主对角线的乘积减去副对角线的乘积;
再看看三阶行列式
举个例子帮助理解
行列式越往高阶越复杂。
二阶和三阶的尚且可以通过上面的方式来暴力求解,但是阶数高了就比较麻烦了。
所以就需要研究行列式的各种性质。
那到底什么是行列式呢?上面的计算方式又是怎么定义的呢?
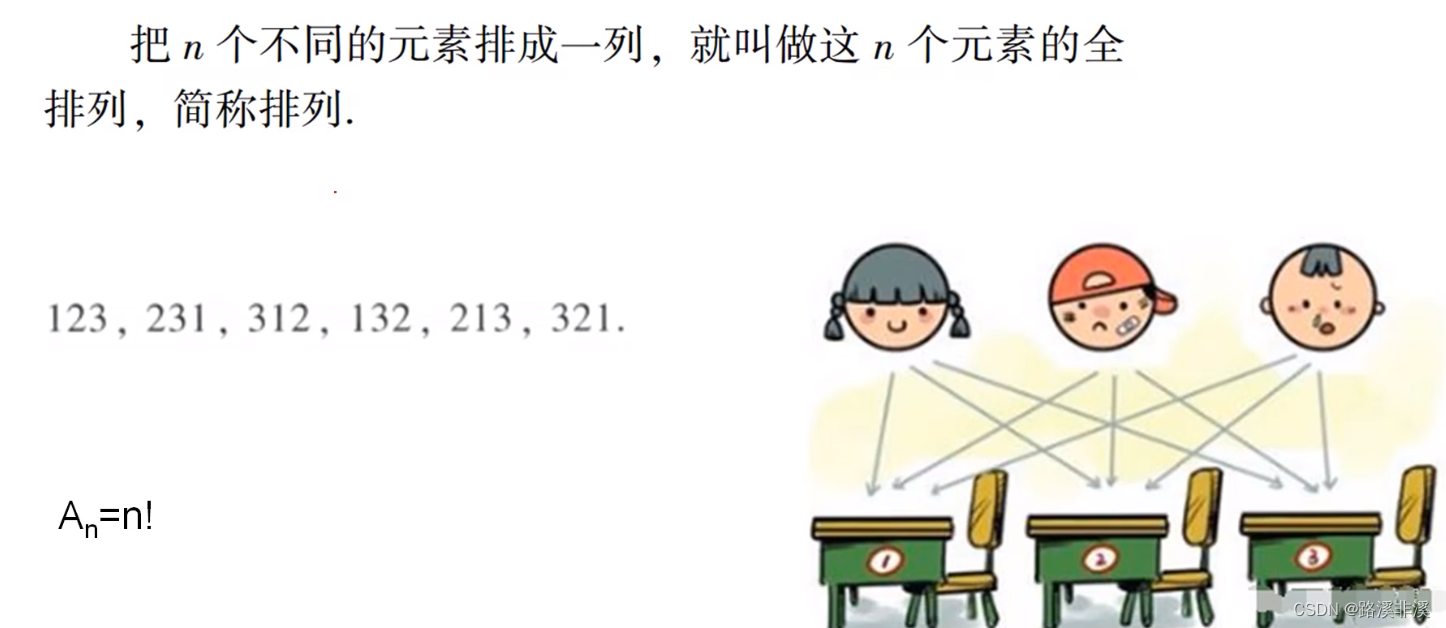
首先,我们回顾下全排列的概念
其实就是一组数有多少种排列组合,其结果就是n的阶乘。
再来看下逆序以及逆序数的概念
逆序是一种状态,而逆序数是指这种状态的数量,要注意区分。
基于全排列和逆序数的概念,我们来看看n阶行列式
n阶行列式就是不同行不同列的所有元素相乘再求和,前面的正负号由逆序数决定,总的求和项就是n的阶乘。
对于行列式,有几个问题一定要注意:
1、行列式是个方形的,行和列数量必须相等,有n行n列,就称之为n阶行列式;
2、行列式两侧用竖线来表示,不能用其他符号;
3、行列式是一个确定的常数;
行列式的定义了解就行,重点记住二阶和三阶的暴力求解方式,然后再记住一些特殊的行列式。
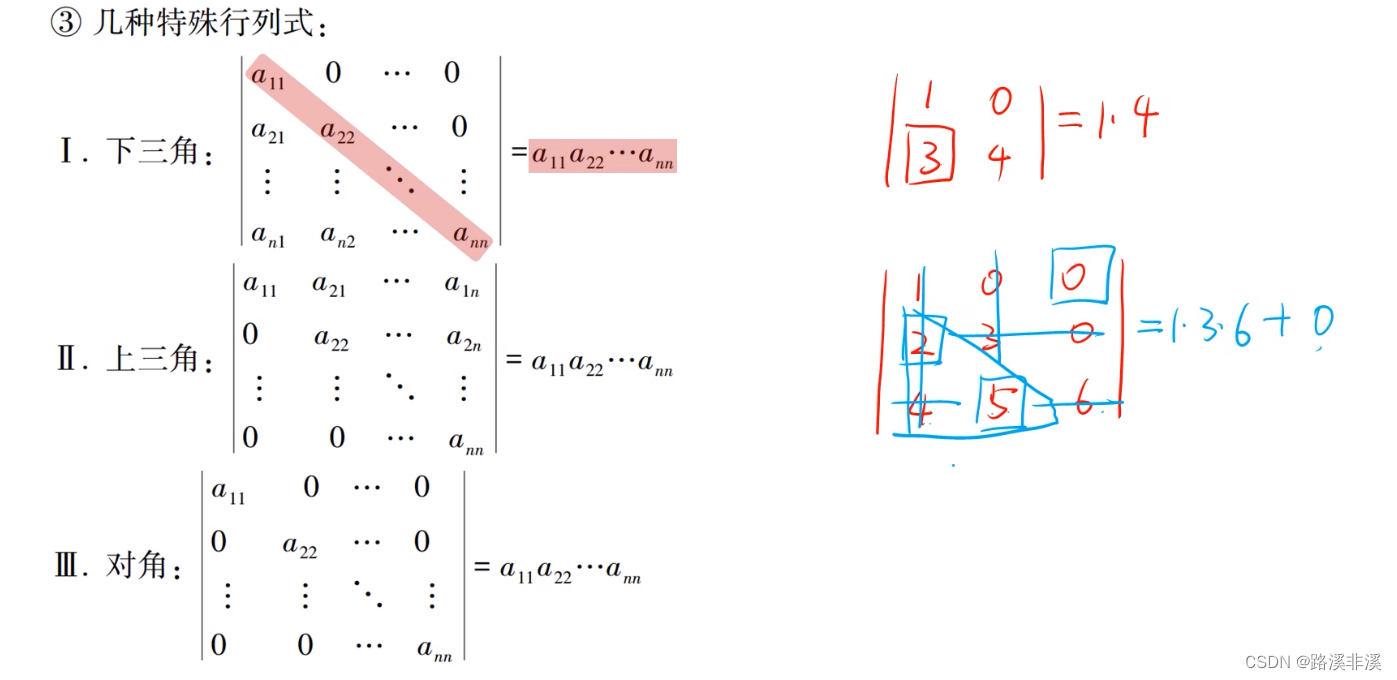
几种特殊行列式
这三种特殊行列式的结果都是主对角线相乘。
行列式的性质
依靠定义很难计算复杂的高阶行列式,所以还需要学习行列式的一些性质。
转置后值不变
转置的符号是右上角加个T
线性性质
线性性质是一大类性质,分为几个小性质
1
注意,对于行和列,都是成立的,行中可以提取k,列中也可以提取k
这个性质有意思的一点是,k可以乘到任意一行或者任意一列。
我们一般称之为倍乘性质。
以二阶行列式为例
三阶也是一样的
注意,这里的粗体a、b、c表示的是向量,我们手写的时候没法表示粗体,所以常常在符号上加一个向右的箭头,表示是个向量。
2
针对某一行或者某一列来拆分的。
还是以二阶举例来加深理解
对换性质
注意,虽然以上描述只讲了两行对换,但是对换行或者列都可以,可能是讲师的PPT写漏了。这个性质我们也可以称之为对换性质。
以二阶为例
对换性质的两条推论
很好理解,因为两行互换后,只有符号相反,用数学语言描述就是x=-x或者x=-kx,此时x只能取0值。
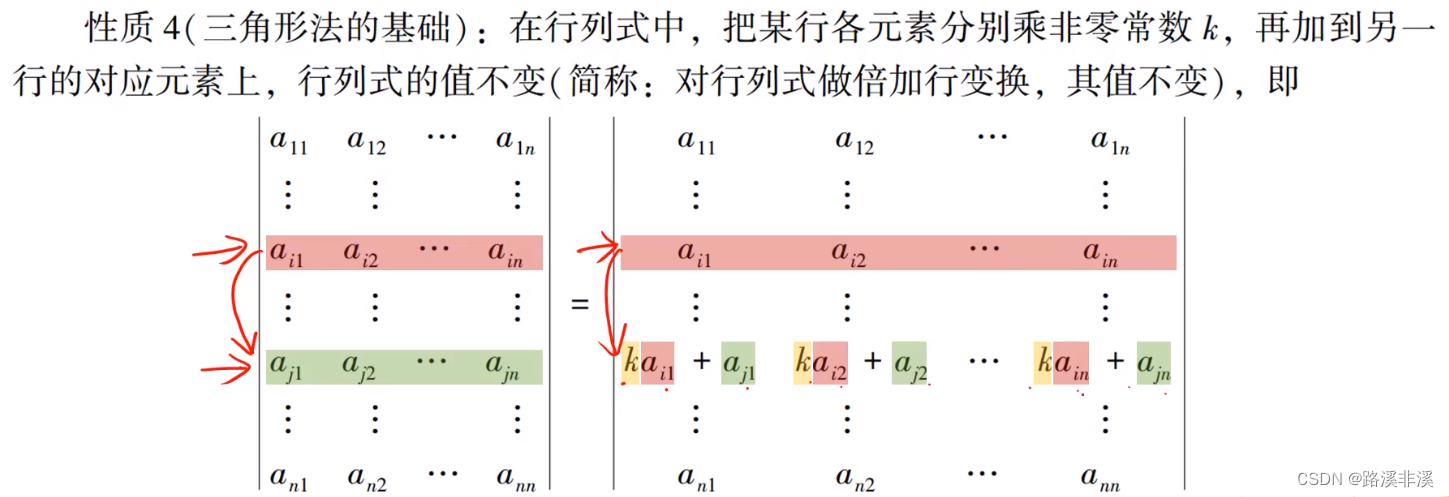
倍加行变换
注意,第i行的值并没有发生改变。
以二阶为例
可以用这个性质对某些元素进行消零。
以上几个性质如果把行列式想象成多元一次方程组来理解,就会发现二者之间是有一些关联的,比如性质4,其实就是将某一个方程整体乘以个系数再和另一个方程相加,从而实现消元。
另外注意,行列式转置后值不变,所以针对行的变换性质针对列也是成立的。
举两个例子
这里几步分别利用的是倍加、倍乘、倍加、上三角的知识。
如果利用定义来暴力求解,那就很麻烦,一般只要超过三阶,就得通过性质来求解。
行列式的展开
仅仅通过定义和行列式的性质,有些高阶行列式也很难求解。
所以,我们就可以研究如何将高阶行列式降成低阶行列式呢?
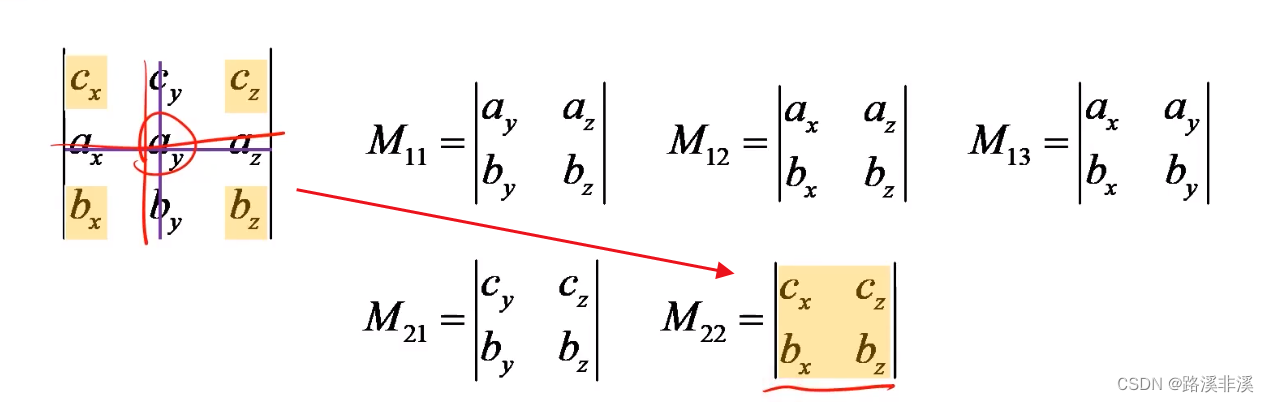
余子式和代数余子式
余子式就是行列式中某个元素去掉该元素所在行所在列之后剩下的元素所组成的行列式;
所以,某个行列式的每个元素都会有一个余子式
代数余子式就是余子式确定前面的正负号之后的余子式。
注意,剩余元素的原顺序不能改变。
代数余子式示例如下:
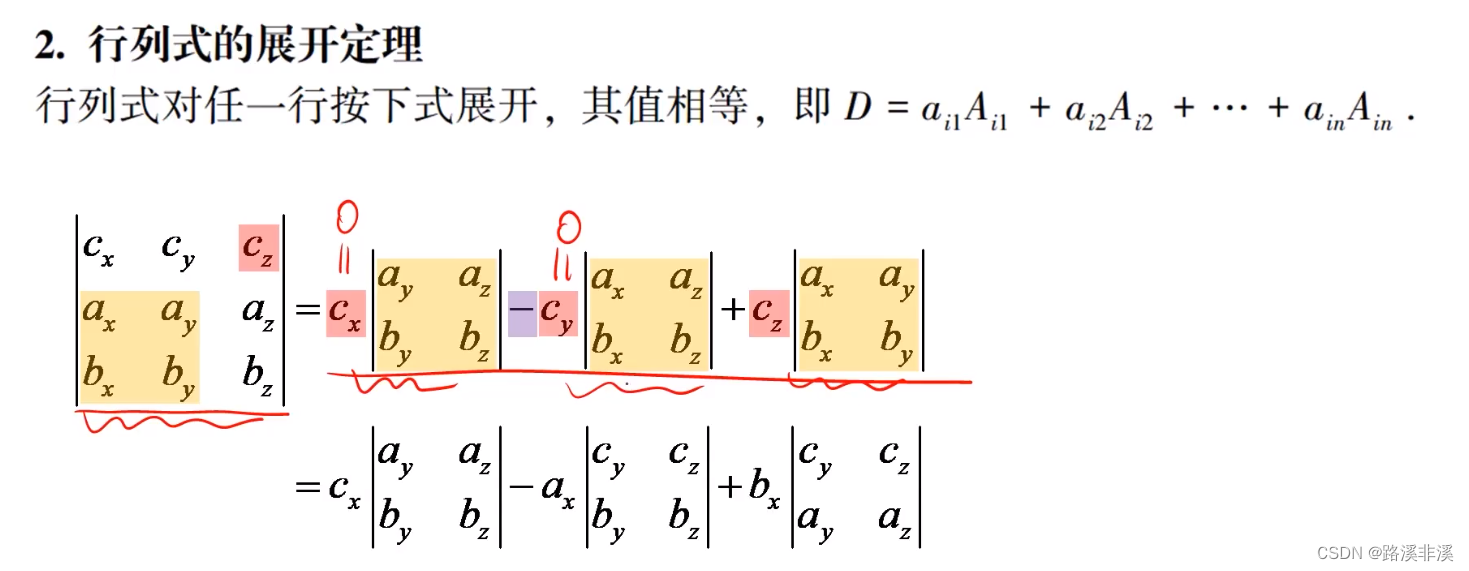
行列式的展开定理
每展开一次,行列式就会降一阶。
实际中,我们常常按照0多的行或者列来展开,能极大简化计算。如果没有0,就看看能不能通过倍加的性质来凑出更多的0
举个简单的例子
范德蒙行列式
范德蒙行列式是由一系列等比数列组成的行列式。
范德蒙行列式的结果就等于所有的公比相减再连乘,相减时一定是下标大的减下标小的。
举个简单的例子
转置后也是同样的结果。
范德蒙行列式就是由行列式展开定理来求得结果的。
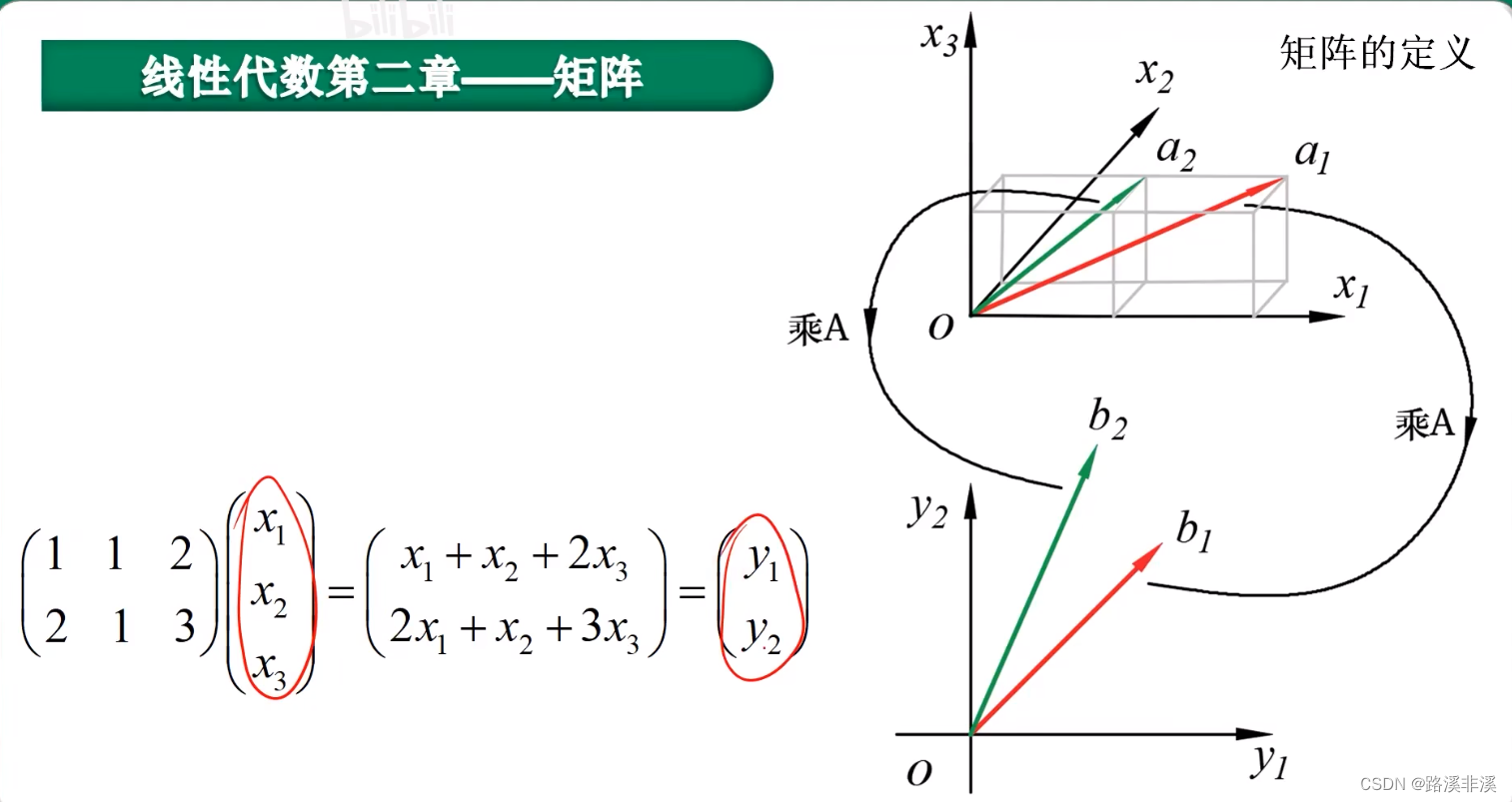
矩阵
注意区分矩阵和行列式。
矩阵的概念和定义
矩阵的定义如下:
几点注意:
1、矩阵只是一个数表,而行列式是一个确定的值,要区分二者的不同;
2、行列式要求必须是n行n列的,而矩阵的行数和列数可以不相等,若相等,可称为方阵;
3、矩阵可以用圆括号括起来,也可以用方括号括起来,注意和行列式的竖线进行区分;
4、注意区分符号和代数余子式的不同,代数余子式是Aij;
矩阵和excel表类似。
同型矩阵和矩阵相等
矩阵的运算
加法
加法的前提是两个矩阵是同型矩阵,然后对应位置的元素值直接相加。
注意和行列式的加和进行区分,行列式只针对某一行或者某一列来加减,而两个矩阵是所有对应元素都要相加。
矩阵加法满足如下运算律
数乘
也要和行列式的倍乘作区分,行列式是某一行或者某一列乘倍数,而矩阵是每一个元素都要乘。
矩阵和矩阵相乘
矩阵和矩阵相乘时,对相乘的两个矩阵是有一定要求的,即要求第一个矩阵的列数和第二个矩阵的行数是相等的。
简单来记忆,就是前者的整行和后者的整列分别相乘,然后放到对应的位置。
这种运算可以叫做内积运算。
注意和两个行列式的相乘进行区分,两个行列式的乘积其实就是两个数的乘积。
矩阵的乘法规则
注意这里的左分配律和右分配率,因为矩阵的左乘和右乘其实并不一定相等,甚至都可能没法相乘,因为反过来不一定能满足矩阵相乘的前提条件。注意和数乘进行区分。
矩阵的转置
求矩阵的行列式
矩阵只有是方阵时,才能求对应的行列式,否则这一运算没有意义。
求逆矩阵
这里的E是单位矩阵,也就是元素都是1的矩阵。
求矩阵的逆,就类似于求一个数的倒数。
矩阵变换的应用
矩阵可以通过运算来实现变换
变换的实际应用举例:
比如图片处理中的线性变换
非线性变换
矩阵还可以提升维度或者降低维度
实际上,我们可以把矩阵看成一个向量组,由一个一个的向量组成;或者我们把矩阵看成一种线性变换,对整个空间实现一种变换。
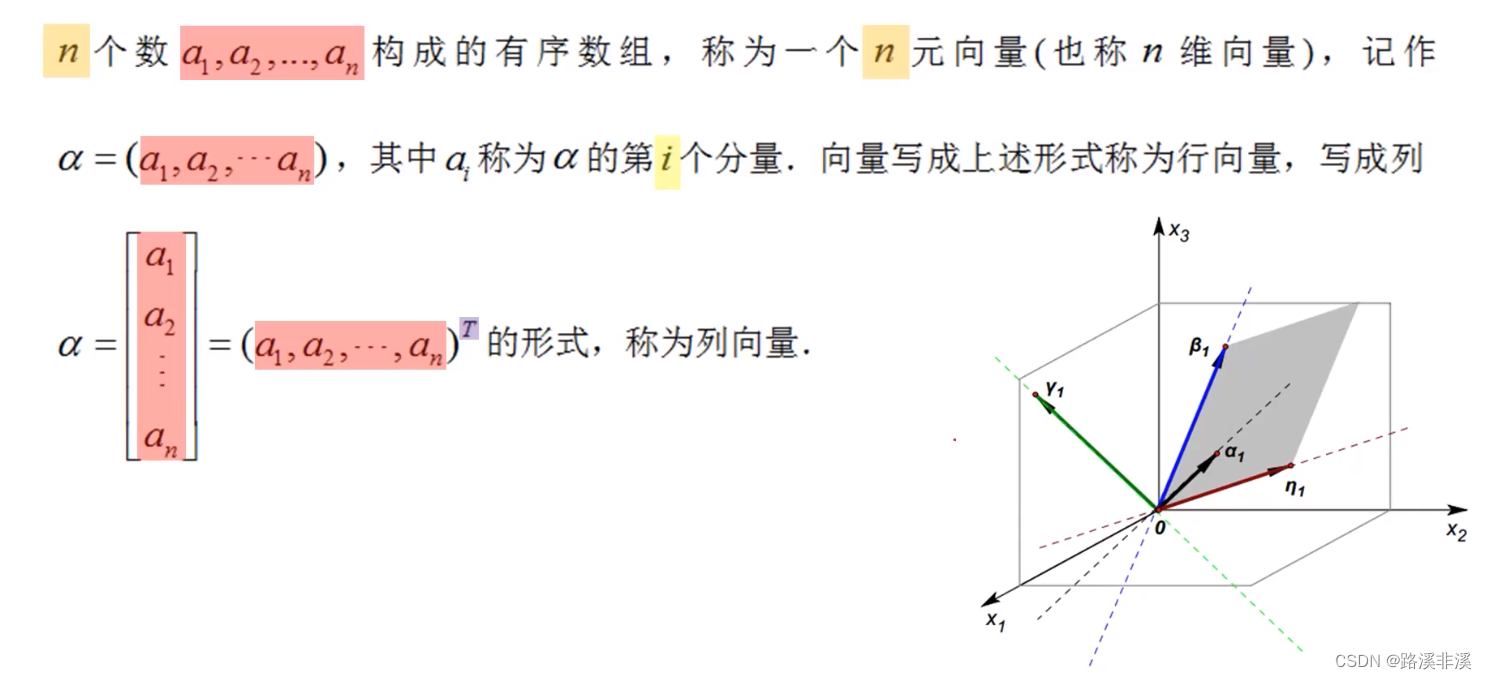
向量
向量其实是一种特殊的矩阵,矩阵可以看做向量的合集。
向量是一种只有一行或者只有一列的矩阵。
向量的基本概念
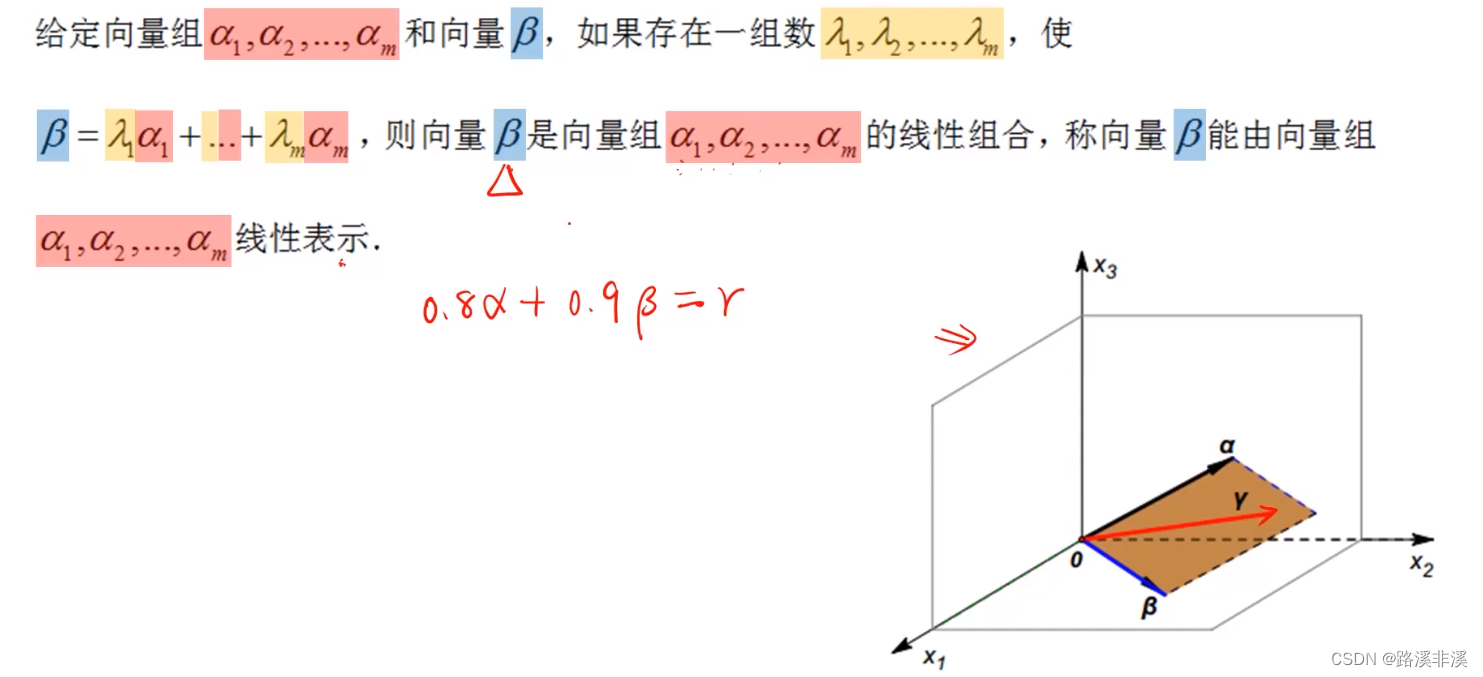
向量组及其线性组合
注意,向量里面的是元素,向量组里面的是向量。
反身性:自己和自己等价;
对称性:α组和β组等价,则β组和α组也等价;
传递性:如果α组和β组等价,β组和γ组等价,则α组和γ组等价。
线性相关
从以上描述可知,线性无关就是,只有当系数全为0时才会满足以上的等式。
相关结论
秩
暂时参考这个视频
第二章 11、矩阵的秩_哔哩哔哩_bilibili
特征值和特征向量
只有矩阵是方阵时,才会研究特征值和特征向量
更多内容需要的时候再补充……







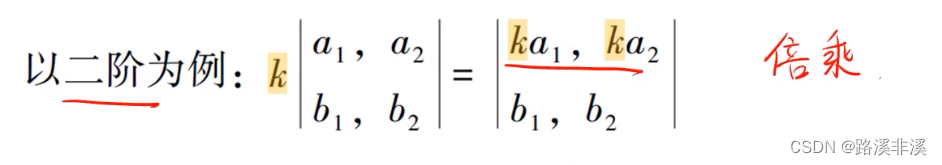
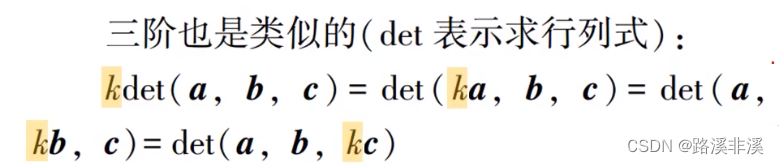

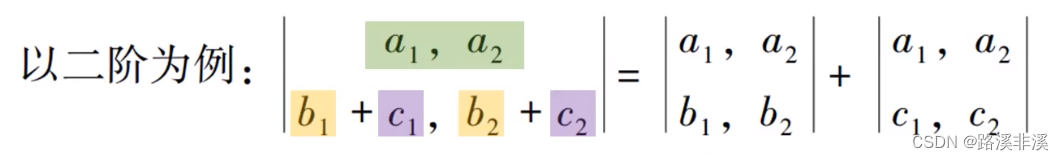



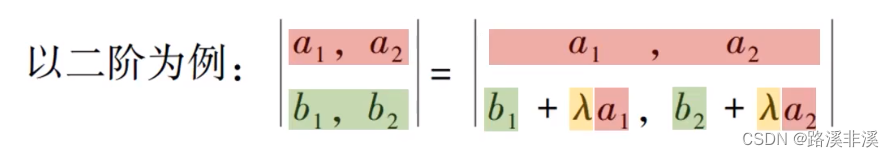


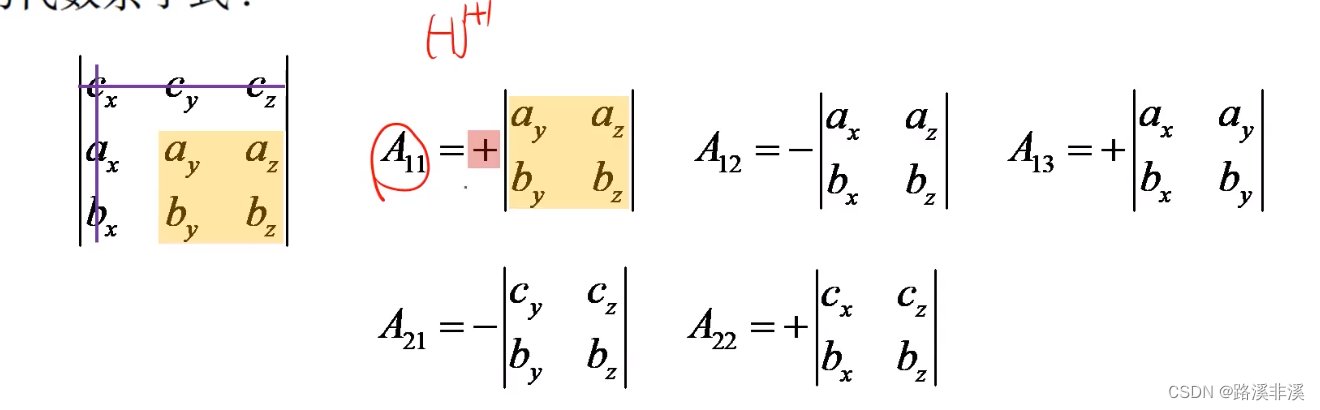


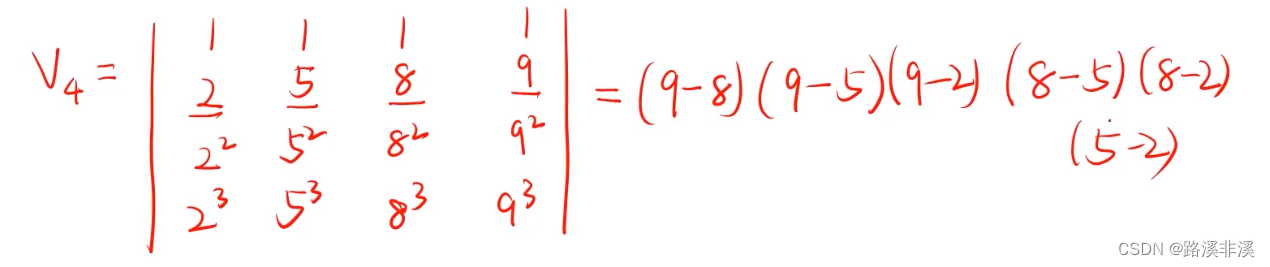







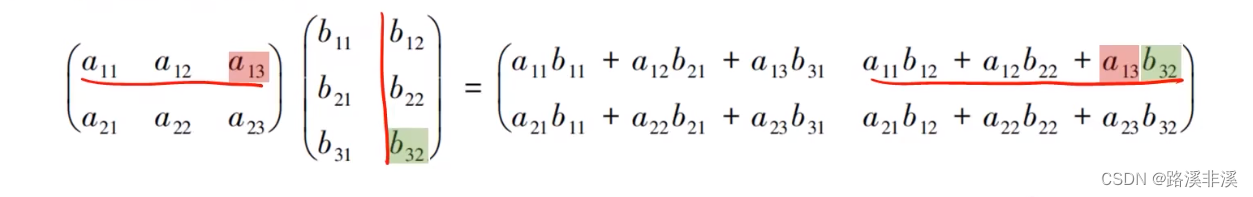





























:一种新颖的模型微调方法)
)

数据准备和数据预处理)


