问你一句:「你知道 HTTP/1.1 该如何优化吗?」

我们可以从下面这三种优化思路来优化 HTTP/1.1 协议:

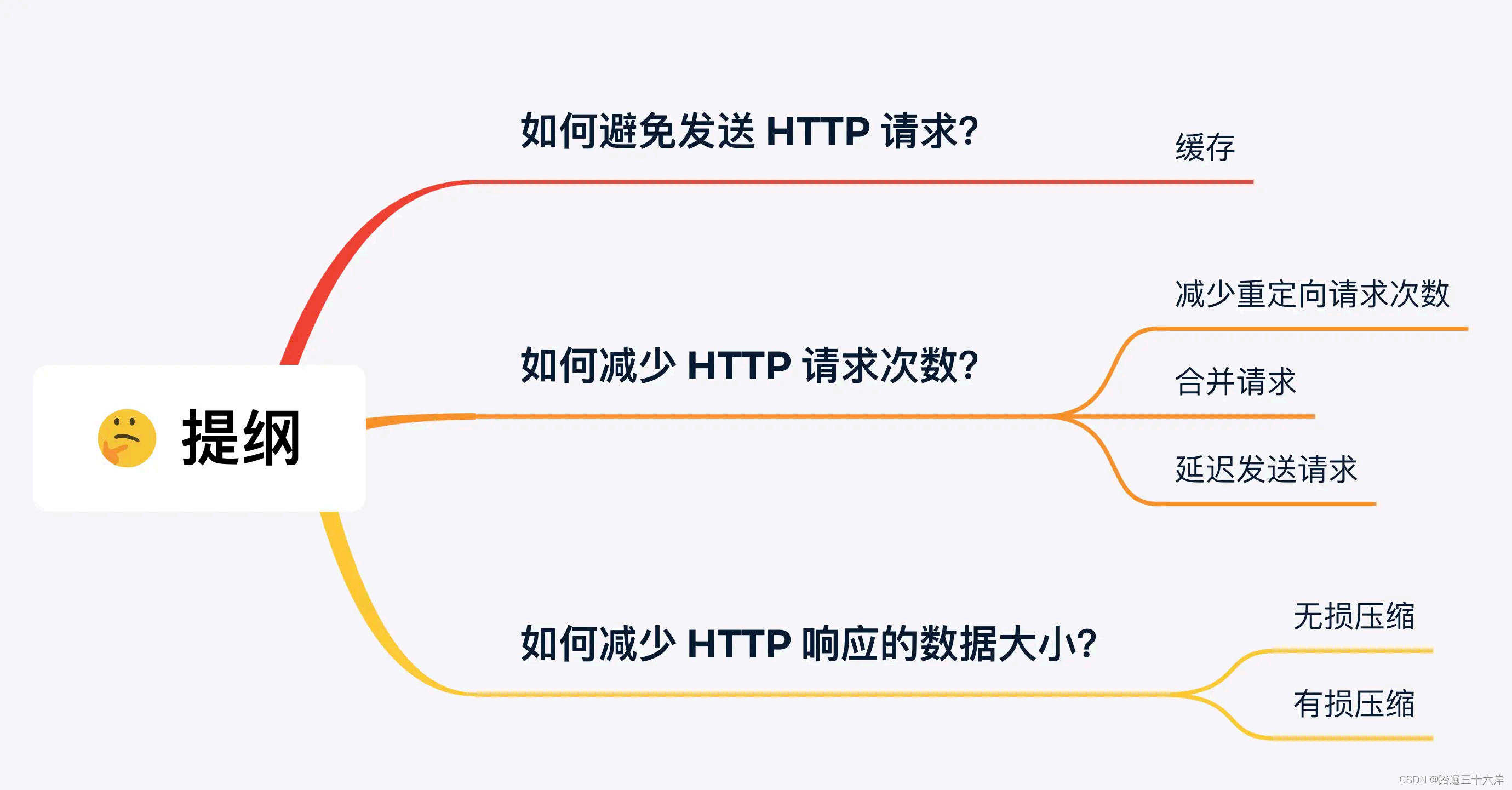
• 尽量避免发送 HTTP 请求
• 在需要发送 HTTP 请求时，考虑如何减少请求次数
• 减少服务器的 HTTP 响应的数据大小

下面，就针对这三种思路具体看看有哪些优化方法，

如何避免发送HTTP请求 : 如何避免发送HTTP请求-CSDN博客

如何减少HTTP请求次数 : 如何减少HTTP请求次数-CSDN博客

如何减少 HTTP 响应的数据大小 : 如何减少 HTTP 响应的数据大小-CSDN博客

总结

这次主要从 3 个方面介绍了优化 HTTP/1.1 协议的思路,

第一个思路是，通过缓存技术来避免发送 HTTP 请求。客户端收到第一个请求的响应后，可以将其缓存在本地磁盘，下次请求的时候，如果缓存没过期，就直接读取本地缓存的响应数据。如果缓存过期，客户端发送请求的时候带上响应数据的摘要，服务器比对后发现资源没有变化，就发出不带包体的 304 响应，告诉客户端缓存的响应仍然有效。

第二个思路是，减少 HTTP 请求的次数，有以下的方法

1. 将原本由客户端处理的重定向请求，交给代理服务器处理，这样可以减少重定向请求的次数
2. 将多个小资源合并成一个大资源再传输，能够减少 HTTP 请求次数以及 头部的重复传输，再来减少TCP 连接数量，进而省去 TCP 握手和慢启动的网络消耗
3. 按需访问资源，只访问当前用户看得到/用得到的资源，当客户往下滑动，再访问接下来的资源，以此达到延迟请求，也就减少了同一时间的 HTTP 请求次数

第三思路是，通过压缩响应资源，降低传输资源的大小，从而提高传输效率，所以应当选择更优秀的压缩算法。

不管怎么优化 HTTP/1.1 协议都是有限的，不然也不会出现 HTTP/2 和 HTTP/3 协议，后续我们再来介绍HTTP/2 和 HTTP/3 协议。

---

这期就到这里,下期见!