相机模型-内参、外参
更多内容,请关注:
github:https://github.com/gotonote/Autopilot-Notes.git)
针孔相机模型,包含四个坐标系:物理成像坐标系、像素坐标系、相机坐标系、世界坐标系。
相机参数包含:内参、外参、畸变参数
一、 内参(Intrinsics)
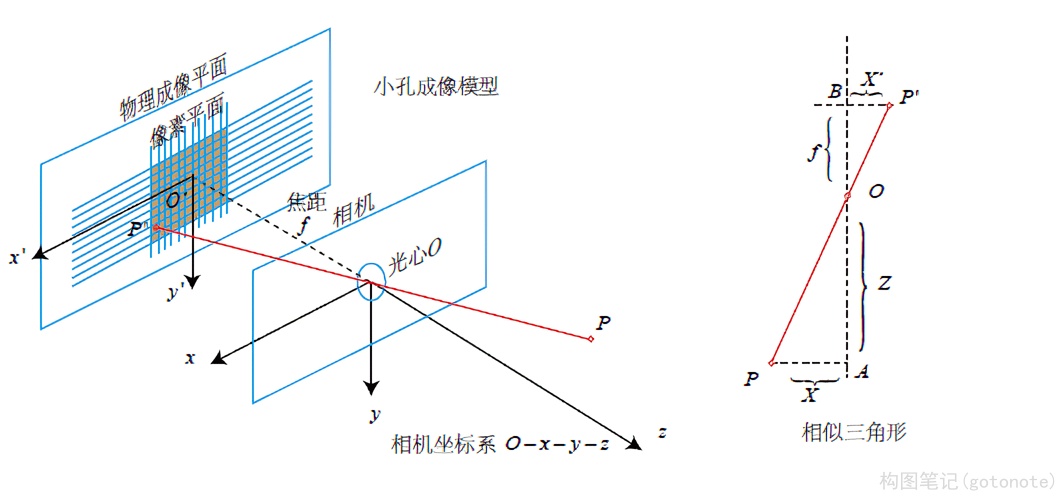
物理成像坐标系: O ′ − x ′ − y ′ O'-x'-y' O′−x′−y′
像素坐标系: O − u − v O-u-v O−u−v
相机坐标系: O − x − y O-x-y O−x−y
世界坐标系: O − X − Y − Z O-X-Y-Z O−X−Y−Z
在世界坐标系下的点 P [ X , Y , Z ] T P[X,Y,Z]^T P[X,Y,Z]T ,通过相机坐标系下的光心 O O O 投影到物理成像平面上的 P ′ [ X ′ , Y ′ , Z ′ ] T P'[X',Y',Z']^T P′[X′,Y′,Z′]T ,对应到像素坐标系下的 [ u , v ] T [u,v]^T [u,v]T 。
由相似三角形可以得到:
Z f = − X X ′ = − Y Y ′ \frac Z f = -\frac X {X'}=-\frac Y {Y'} fZ=−X′X=−Y′Y
带负号是因为小孔成像成的是倒像。为了简化模型,可以把物理成像平面看作为放到了相机的前方,这样可以直观的认为成立的正像(虚像),如下图2:

可以得到:
Z f = X X ′ = Y Y ′ \begin{align} \frac Z f = \frac X {X'}=\frac Y {Y'} \end{align} fZ=X′X=Y′Y
X ′ = f X Z \begin{align} X'=f\frac X Z \end{align} X′=fZX
Y ′ = f Y Z \begin{align} Y'=f\frac Y Z \end{align} Y′=fZY
从物理成像坐标系到像素坐标系之前,相差了一个缩放和平移。缩放是因为两个坐标系之前的表示的单位长度不一致,平移是因为两个坐标系的原点不一致。
假设,像素坐标在 u u u 方向上缩放了 α \alpha α 倍,在 v v v 方向上缩放了 β \beta β 倍,同时,原点平移了 [ c x , c y ] T [c_x,c_y]^T [cx,cy]T 。那么点 P ′ [ X ′ , Y ′ , Z ′ ] T P'[X',Y',Z']^T P′[X′,Y′,Z′]T 与像素坐标系下 [ u , v ] T [u,v]^T [u,v]T 的关系为:
{ u = α X ′ + c x v = β Y ′ + c y \begin{cases} u=\alpha X'+c_x \\ v=\beta Y'+c_y \end{cases} {u=αX′+cxv=βY′+cy
f x = α f f_x = \alpha f fx=αf
f y = β f f_y = \beta f fy=βf
{ u = f x X Z + c x v = f y Y Z + c y \begin{cases} u=f_x \frac XZ + c_x \\ v=f_y \frac YZ + c_y \end{cases} {u=fxZX+cxv=fyZY+cy
其中,变量的单位是 f → m m ; α , β → 像素 / m m ; f x , f y → 像素 f \rightarrow mm ; \alpha, \beta \rightarrow 像素/mm; f_x,f_y \rightarrow 像素 f→mm;α,β→像素/mm;fx,fy→像素。将坐标进行归一化,写成矩阵形式,并对左侧像素坐标进行齐次化,方便后面的运算:
[ u v 1 ] = 1 Z [ f x 0 c x 0 f y c y 0 0 1 ] P = △ 1 Z K P \begin{bmatrix} u \\ v \\ 1 \\ \end{bmatrix} = \frac 1Z \begin{bmatrix} f_x &0 &c_x \\ 0 &f_y &c_y\\ 0 &0 &1 \\ \end{bmatrix} \boldsymbol{P} \overset{\triangle}{=} \frac1Z \boldsymbol{KP} uv1 =Z1 fx000fy0cxcy1 P=△Z1KP
Z [ u v 1 ] = [ f x 0 c x 0 f y c y 0 0 1 ] P = △ K P {Z}\begin{bmatrix} u \\ v \\ 1 \\ \end{bmatrix} = \begin{bmatrix} f_x &0 &c_x \\ 0 &f_y &c_y \\ 0 &0 &1 \\ \end{bmatrix} \boldsymbol{P} \overset{\triangle}{=} \boldsymbol{KP} Z uv1 = fx000fy0cxcy1 P=△KP
把中间的量组成的矩阵称为相机的内参矩阵(Camera Intrinsics) K \boldsymbol K K 。
(一) 内参矩阵参数获取

图像大小 [ w , h ] [w,h] [w,h] ,单位 p i x e l pixel pixel ;相机焦距 f f f ,单位 m m mm mm ;视场角 F O V − α FOV-\alpha FOV−α ,单位弧度;像素单元长度 d x , d y \mathrm{d}x,\mathrm{d}y dx,dy ,单位 m m / p i x e l mm/pixel mm/pixel ;内参 $f_x,f_x $,单位 p i x e l pixel pixel :
f x = f d x \boldsymbol{f_x=\frac f{\mathrm{d}x}} fx=dxf
f y = f d y \boldsymbol{f_y=\frac f{\mathrm{d}y}} fy=dyf
c x = w 2 ( 假设相机主点在图像中央 ) \boldsymbol{c_x=\frac w2} \ (假设相机主点在图像中央) cx=2w (假设相机主点在图像中央)
c y = h 2 ( 假设相机主点在图像中央 ) \boldsymbol{c_y =\frac h2} \ (假设相机主点在图像中央) cy=2h (假设相机主点在图像中央)
f x \boldsymbol {f_x} fx就相当于用 x x x 方向的像素数去量化物理焦距 f f f ;
f y \boldsymbol {f_y} fy就相当于用 y y y 方向的像素数去量化物理焦距 f f f ;

1. 已知相机的硬件参数求内参
相机的内参出厂后就是固定不变的,如果知晓相机的出厂参数,可以计算相机的内参。
如成像传感器是 m × n ( μ m ) m\times n(\mu m) m×n(μm) ,图像尺寸是 w × h ( p i x e l ) w\times h(pixel) w×h(pixel) ,那么图像像素单元就是
d x = m w ( μ m / p i x e l ) \mathrm{d}x=\frac mw(\mu m/pixel) dx=wm(μm/pixel)
d y = n h ( μ m / p i x e l ) \mathrm{d}y=\frac nh(\mu m/pixel) dy=hn(μm/pixel)
c x = w 2 c y = h 2 c_x=\frac w2 \\ c_y =\frac h2 cx=2wcy=2h
如果 d x = d y \mathrm{d}x=\mathrm{d}y dx=dy ,则图像像素单元是一个正方形,此时 f x = f y \boldsymbol {f_x=f_y} fx=fy ;
如果 d x ≠ d y \mathrm{d}x \neq \mathrm{d}y dx=dy ,则图像像素单元是一个矩形,此时 f x ≠ f y \boldsymbol {f_x \neq f_y} fx=fy 。
如成像传感器是 2000 × 1000 ( μ m ) 2000\times 1000(\mu m) 2000×1000(μm) ,图像尺寸是 1000 × 500 ( p i x e l ) 1000\times 500(pixel) 1000×500(pixel) ,那么图像像素单元就是 d x = d y = 2 ( μ m / p i x e l ) \mathrm{d}x=\mathrm{d}y=2(\mu m/pixel) dx=dy=2(μm/pixel) , c x = 500 , c y = 250 ( p i x e l ) c_x=500,c_y=250(pixel) cx=500,cy=250(pixel) 。
2. 求视场角 FOV
这里只是求水平方向上的 FOV,垂直方向上的 FOV 求法和水平是一致的。
(参考图3)其中,成像传感器是 m × n ( μ m ) m\times n(\mu m) m×n(μm) ,图像尺寸是 w × h ( p i x e l ) w\times h(pixel) w×h(pixel) ,像素单元 x x x 轴方向长度 d x = m w ( μ m / p i x e l ) \mathrm{d}x=\frac mw(\mu m/pixel) dx=wm(μm/pixel) ,可以看到:
tan ( α 2 ⋅ π 180 ) = m / 2 f \begin{align} \tan({\frac {\alpha}2} \cdot \frac {\pi}{180} ) = \frac {m/2}{f} \end{align} tan(2α⋅180π)=fm/2
F O V = α = 2 arctan ( m / 2 f ) ⋅ 180 π \begin{align} FOV=\alpha = 2\arctan(\frac {m/2}{f}) \cdot \frac {180}{\pi} \end{align} FOV=α=2arctan(fm/2)⋅π180
m = w ⋅ d x m =w\cdot \mathrm{d}x m=w⋅dx
F O V = α = 2 arctan ( w ⋅ d x / 2 f ) ⋅ 180 π FOV=\alpha =2\arctan(\frac {w\cdot \mathrm dx/2}{f}) \cdot \frac {180}{\pi} FOV=α=2arctan(fw⋅dx/2)⋅π180
f x = f d x f_x = \frac f{\mathrm dx} fx=dxf
F O V = α = 2 arctan ( w 2 f x ) ⋅ 180 π \begin{align} FOV=\alpha =2\arctan(\frac {w}{2f_x}) \cdot \frac {180}{\pi} \end{align} FOV=α=2arctan(2fxw)⋅π180
如果已知相机传感器尺寸,通过公式 (5) 可以计算出相机的视场角 F O V FOV FOV ;
如果已知相机内参,通过公式 (6) 可以计算出相机的视场角 F O V FOV FOV 。
3. 通过 FOV 计算内参
由公式 (6),可得:
w 2 f x = tan ( F O V 2 ⋅ π 180 ) \frac{w}{2f_x} = \tan(\frac {FOV}{2} \cdot \frac {\pi}{180}) 2fxw=tan(2FOV⋅180π)
f x = w 2 tan ( F O V 2 ⋅ π 180 ) f_x = \frac w{2\tan(\frac {FOV}{2} \cdot \frac {\pi}{180})} fx=2tan(2FOV⋅180π)w
f y = h 2 tan ( F O V 2 ⋅ π 180 ) f_y = \frac h{2\tan(\frac {FOV}{2} \cdot \frac {\pi}{180})} fy=2tan(2FOV⋅180π)h
如果 d x = d y \mathrm{d}x=\mathrm{d}y dx=dy ,则图像像素单元是一个正方形,此时 f x = f y \boldsymbol {f_x=f_y} fx=fy ; c x = w 2 \boldsymbol {c_x=\frac w2 } cx=2w ; c y = h 2 \\ \boldsymbol {c_y =\frac h2} cy=2h 。
二、 外参 (Extrinsics)
相机外参的逆矩阵被称为camera-to-world (c2w)矩阵,其作用是把相机坐标系的点变换到世界坐标系。因为NeRF主要使用c2w,这里详细介绍一下c2w的含义。c2w矩阵是一个4x4的矩阵,左上角3x3是旋转矩阵R,右上角的3x1向量是平移向量T。有时写的时候可以忽略最后一行 [0,0,0,1] 。c2w矩阵的值直接描述了相机坐标系的朝向和原点:
$$
\left[
\begin{matrix}
R & T \
0 & 1 \
\end{matrix}
\right]
\left[
\begin{matrix}
r_{11} & r_{12} & r_{13} & t_1 \
r_{21} & r_{22} & r_{23} & t_2 \
r_{31} & r_{32} & r_{33} & t_3 \
0 & 0 & 0 & 1 \
\end{matrix}
\right]
$$
$$
\left[
\begin{matrix}
R & T \
\end{matrix}
\right]
\left[
\begin{matrix}
r_{11} & r_{12} & r_{13} & t_1 \
r_{21} & r_{22} & r_{23} & t_2 \
r_{31} & r_{32} & r_{33} & t_3 \
\end{matrix}
\right]
$$
具体的,旋转矩阵的第一列到第三列分别表示了相机坐标系的 X, Y, Z 轴在世界坐标系下对应的方向;平移向量表示的是相机原点在世界坐标系的对应位置。
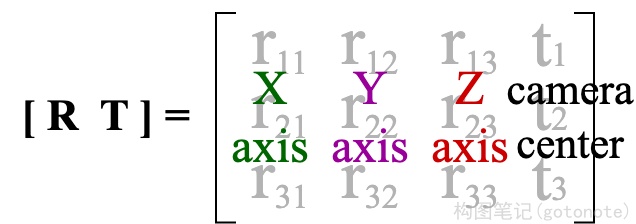
相机内参描述的是在相机坐标系下的点到像素坐标系下的对应关系,上文内提到的 P \boldsymbol P P 也是在相机坐标系下的点。相机在三维空间中运动,记点 P \boldsymbol P P 在世界坐标系下的点为 P w \boldsymbol P_w Pw ,在相机坐标系下的坐标为 P c \boldsymbol P_c Pc 。
相机在世界坐标系下的位姿,由相机的旋转矩阵 R \boldsymbol R R 和平移向量 t \boldsymbol t t 来描述。此时有( 以下用 T 3 × 4 \boldsymbol{T_{3\times4}} T3×4 代表 [ R T ] [R \ \ T] [R T] ):
Z ⋅ P u v ∣ 3 × 1 {Z} \cdot \boldsymbol {P_{uv} |_{3\times1}} Z⋅Puv∣3×1
= Z ⋅ [ u v 1 ] {= Z} \cdot \left[ \begin{matrix} u \\ v \\ 1 \\ \end{matrix} \right] =Z⋅ uv1
= K ( R P w + t ) {=} \boldsymbol{K} (\boldsymbol{RP_w+t}) =K(RPw+t)
= K 3 × 3 ⋅ T 3 × 4 ⋅ P w 4 × 1 \begin{align} {=} \boldsymbol{K_{3\times3}} \cdot \boldsymbol{T_{3\times4}} \cdot \boldsymbol{{P_w} \ _{4\times1}} \end{align} =K3×3⋅T3×4⋅Pw 4×1
两侧都是齐次坐标,同时因为齐次坐标乘上非零常数后表达同样的含义,所以可以简单地把Z去掉:
P u v = K T P w \boldsymbol {P_{uv}= KTP_w} Puv=KTPw
但这样等号意义就变了,成为在齐次坐标下相等的概念,相差了一个非零常数。为了避免麻烦,我们还是从传统意义下来定义书写等号。
式 (7) 表明,我们可以把一个世界坐标点先转换到相机坐标系,再除掉它最后一维的数值(该点距离相机成像平面的深度),这就相当于把最后一维进行了 归一化处理 ,得到点 P P P 在相机 归一化平面 上的投影:
( R P w + t ) = [ X , Y , Z ] T → [ X / Z , Y / Z , 1 ] T ( 相机坐标 → 归一化坐标 ) (\boldsymbol {RP_w+t}) \ \ \ \ {=} \ \ \ [X,Y,Z]^T \ \ \ \to \ \ \ \ [X/Z,Y/Z,1]^T \\ \ \ \ \ ({相机坐标} \ \ \to \ \ {归一化坐标}) (RPw+t) = [X,Y,Z]T → [X/Z,Y/Z,1]T (相机坐标 → 归一化坐标)
归一化坐标 可以看成相机前方 Z = 1 Z=1 Z=1 处的平面上的一个点,这个 Z = 1 Z=1 Z=1 平面也称为 归一化平面 。归一化坐标左称内参 K \boldsymbol K K 就得到了像素坐标,因此可以把像素坐标 [ u , v ] T [u,v]^T [u,v]T 看成对归一化平面上的点进行量化测量的结果。
同时可以看到,如果对相机坐标同时乘上任意非零常数,归一化坐标都是一样的,也就是 点的深度信息在投影的过程中丢失了 ,所以在单目视觉中没法得到像素点的深度值。
通过最终的转换关系来看,一个三维中的坐标点,的确可以在图像中找到一个对应的像素点,但是反过来,通过图像中的一个点找到它在三维中对应的点就很成了一个问题,因为我们并不知道等式左边的 z c z_c zc(深度值)的值。

 is undefined for the type Stream)

)
 数据同化思路)
)

:神经网络之推荐系统处理)


)

- 一致性hash)
)



)

