今天我们来学习bfs的反向搜索。

1.反向搜索

反向搜索：是从目标状态出发进行的搜索，一般用于终点状态唯一，起点状态有多种，且状态转移是可逆的（无向边）情况。

例题：在一个长度为 n 的坐标轴上，有一个非常特别的整数位置 T。蒜头君有 Q 次询问，每次询问蒜头君想要知道从整数位置 S 移动到整数位置 T 的最少移动次数。

他的移动规则如下：

1. 向前一步，坐标增加 1

2. 向后一步，坐标减少 1 

3. 跳跃一步，使得坐标乘 2

蒜头君不能移动到坐标小于 
0 或大于 n 的位置。（0≤S,T≤n≤5000,1≤Q≤10的4次方）

按照之前我们学习的课程，对于每次询问，当我们获得 
S 后，可以按照移动规则使用 BFS 计算出 
S→T 的最少移动次数。

下图为 S 分别等于1,3，T=4 的情况。

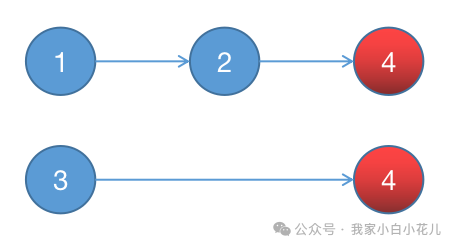
因为每次询问我们都需要进行 BFS，所以程序是十分低效的。

我们可以发现终点 
T 是唯一的，所以我们可以考虑从 T 开始进行反向搜索，计算出 T 到达每个位置的最短距离 dis[]，当我们在输入 S 进行查询时，直接输出 dis[S] 的值即可。（注：S→T 的最短距离等于 
T→S的最短距离）

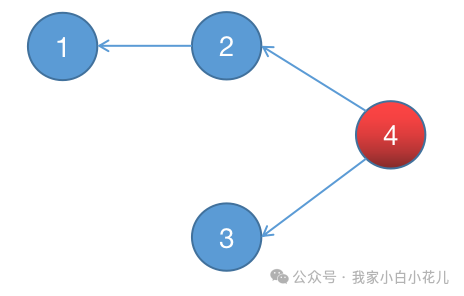
但是在搜索的过程中，我们需要改变移动规则（与原规则 
1,2,3 对应）：

1. 向后一步，坐标减少 1。

2. 向前一步，坐标增加 1。

3. 如果当前位置为偶数，则跳跃一步，使得坐标除 2；否则不执行

那我们就来使用反向搜索来解决《一维坐标的移动》这道题目。

#include <cstdio>
#include <cstring>
#include <iostream>
#include <queue>
using namespace std;
int n, dis[5005];
queue < int > q;
void bfs(int start) {memset(dis, -1, sizeof(dis));dis[start] = 0;q.push(start);while (!q.empty()) {int now = q.front();q.pop();if (now - 1 >= 0 && dis[now - 1] == -1) {dis[now - 1] = dis[now] + 1;q.push(now - 1);}if (now + 1 <= n && dis[now + 1] == -1) {dis[now + 1] = dis[now] + 1;q.push(now + 1);}if (now != 0 && now % 2 == 0 && dis[now / 2] == -1) {dis[now / 2] = dis[now] + 1;q.push(now / 2);}}
}
int main() {freopen("move.in", "r", stdin);freopen("move.out", "w", stdout);int Q, T;cin >> n >> T >> Q;bfs(T);while (Q--) {int S;cin >> S;cout << dis[S] << endl;}return 0;
}