算法学习——LeetCode力扣回溯篇3

算法学习——LeetCode力扣回溯篇3

在这里插入图片描述

491. 非递减子序列

491. 非递减子序列 - 力扣（LeetCode）

描述

给你一个整数数组 nums ，找出并返回所有该数组中不同的递增子序列，递增子序列中 至少有两个元素 。你可以按 任意顺序 返回答案。

数组中可能含有重复元素，如出现两个整数相等，也可以视作递增序列的一种特殊情况。

示例

示例 1：

输入：nums = [4,6,7,7]
输出：[[4,6],[4,6,7],[4,6,7,7],[4,7],[4,7,7],[6,7],[6,7,7],[7,7]]

示例 2：

输入：nums = [4,4,3,2,1]
输出：[[4,4]]

提示

  • 1 <= nums.length <= 15
  • -100 <= nums[i] <= 100

代码解析

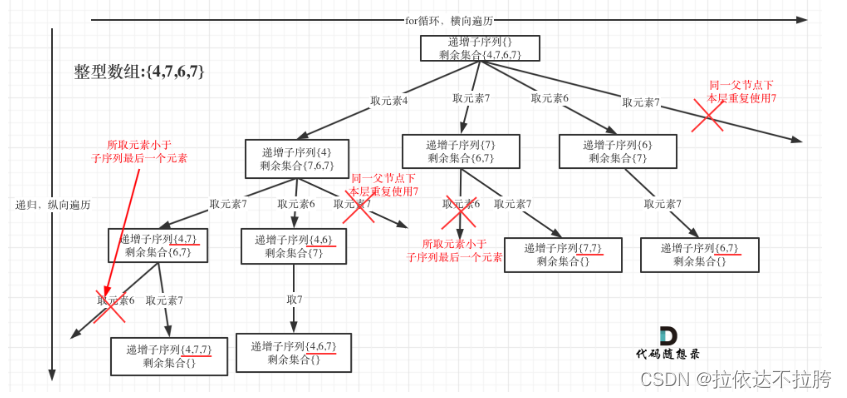
在这里插入图片描述

class Solution {
public:vector<vector<int>> result;vector<int> path;void backtracking(vector<int>& nums , int indnx ){//小于2的不加入结果，至少两个if(path.size()>=2) result.push_back(path);if(indnx >= nums.size()) return;//用set统计每一层相同值元素的使用unordered_set<int> uset;for(int i =indnx ; i<nums.size(); i++){//如果当前值小于上一个，或者这个值在该层用过了，跳过if(path.empty() == 0 && nums[i] < path.back() || uset.find(nums[i]) != uset.end()) continue;//将该使用过的存入set，标记使用过uset.insert(nums[i]);path.push_back(nums[i]);backtracking(nums,i+1 );path.pop_back();}return;}vector<vector<int>> findSubsequences(vector<int>& nums) {backtracking(nums,0);return result;}
};

46. 全排列

46. 全排列 - 力扣（LeetCode）

描述

给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

示例

示例 1：

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

示例 2：

输入：nums = [0,1]
输出：[[0,1],[1,0]]

示例 3：

输入：nums = [1]
输出：[[1]]

提示

  • 1 <= nums.length <= 6
  • -10 <= nums[i] <= 10
  • nums 中的所有整数 互不相同

代码解析

回溯法
class Solution {
public:vector<vector<int>> result;vector<int> path;void backtracking(vector<int> &nums){if(path.size() == nums.size()){result.push_back(path);return;} for(int i = 0 ; i<nums.size() ; i++){auto it = find(path.begin(),path.end(),nums[i]);//如果这个元素在这个树枝之前用过，就跳出if(it == path.end()) {path.push_back(nums[i]);}else{continue;}backtracking(nums);path.pop_back();}return;}vector<vector<int>> permute(vector<int>& nums) {backtracking(nums);return result;}
};
回溯标记法

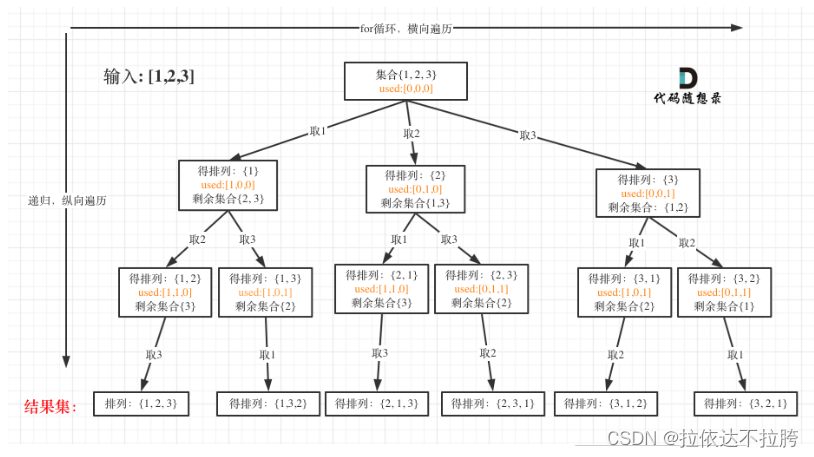
在这里插入图片描述

class Solution {
public:vector<vector<int>> result;vector<int> path;void backtracking (vector<int>& nums, vector<bool>& used) {// 此时说明找到了一组if (path.size() == nums.size()) {result.push_back(path);return;}for (int i = 0; i < nums.size(); i++) {if (used[i] == true) continue; // path里已经收录的元素，直接跳过used[i] = true;path.push_back(nums[i]);backtracking(nums, used);path.pop_back();used[i] = false;}}vector<vector<int>> permute(vector<int>& nums) {result.clear();path.clear();vector<bool> used(nums.size(), false);backtracking(nums, used);return result;}
};

47. 全排列 II

47. 全排列 II - 力扣（LeetCode）

描述

给定一个可包含重复数字的序列 nums ，按任意顺序 返回所有不重复的全排列。

示例

示例 1：

输入：nums = [1,1,2]
输出：
[[1,1,2],
[1,2,1],
[2,1,1]]

示例 2：

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

提示

  • 1 <= nums.length <= 8
  • -10 <= nums[i] <= 10

代码解析

回溯标记法（不去重，时间复杂度高）

在插入之前做一个find查找，找不到相同的插入

class Solution {
public:vector<vector<int>> result;vector<int> path;void backtracking(vector<int>& nums , vector<bool>& used){if(path.size() == nums.size()){if(find(result.begin() , result.end() , path) == result.end() ) result.push_back(path);return;}for(int i=0 ; i<nums.size() ;i++){if(used[i] == 1) continue;used[i]=1;path.push_back(nums[i]);backtracking(nums,used);path.pop_back();used[i]=0;}return;}vector<vector<int>> permuteUnique(vector<int>& nums) {vector<bool> used(nums.size(),false);backtracking(nums,used);return result;}
};
回溯去重
class Solution {
private:vector<vector<int>> result;vector<int> path;void backtracking (vector<int>& nums, vector<bool>& used) {// 此时说明找到了一组if (path.size() == nums.size()) {result.push_back(path);return;}for (int i = 0; i < nums.size(); i++) {// used[i - 1] == true，说明同一树枝nums[i - 1]使用过// used[i - 1] == false，说明同一树层nums[i - 1]使用过// 如果同一树层nums[i - 1]使用过则直接跳过if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) //去重{continue;}if (used[i] == false) {used[i] = true;path.push_back(nums[i]);backtracking(nums, used);path.pop_back();used[i] = false;}}}
public:vector<vector<int>> permuteUnique(vector<int>& nums) {result.clear();path.clear();sort(nums.begin(), nums.end()); // 排序vector<bool> used(nums.size(), false);backtracking(nums, used);return result;}
};
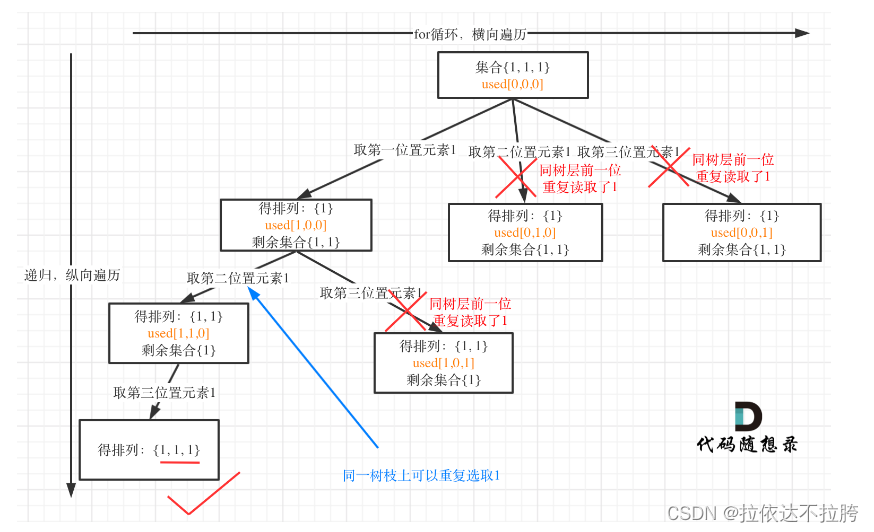
树层去重
if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false)
{continue;
}

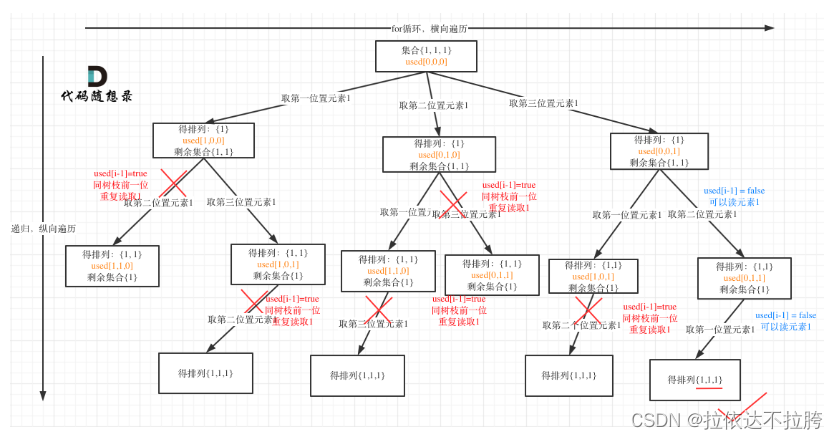
在这里插入图片描述

树枝去重
if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == true)
{continue;
}

在这里插入图片描述

332. 重新安排行程

332. 重新安排行程 - 力扣（LeetCode）

描述

给你一份航线列表 tickets ，其中 tickets[i] = [fromi, toi] 表示飞机出发和降落的机场地点。请你对该行程进行重新规划排序。

所有这些机票都属于一个从 JFK（肯尼迪国际机场）出发的先生，所以该行程必须从 JFK 开始。如果存在多种有效的行程，请你按字典排序返回最小的行程组合。

例如，行程 [“JFK”, “LGA”] 与 [“JFK”, “LGB”] 相比就更小，排序更靠前。
假定所有机票至少存在一种合理的行程。且所有的机票 必须都用一次 且 只能用一次。

示例

示例 1：
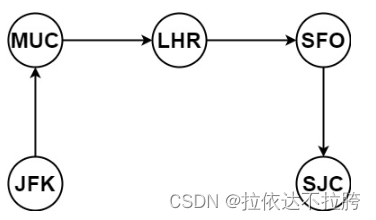
在这里插入图片描述

输入：tickets = [[“MUC”,“LHR”],[“JFK”,“MUC”],[“SFO”,“SJC”],[“LHR”,“SFO”]]
输出：[“JFK”,“MUC”,“LHR”,“SFO”,“SJC”]

示例 2：

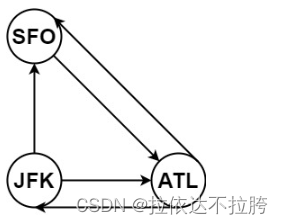
在这里插入图片描述

输入：tickets = [[“JFK”,“SFO”],[“JFK”,“ATL”],[“SFO”,“ATL”],[“ATL”,“JFK”],[“ATL”,“SFO”]]
输出：[“JFK”,“ATL”,“JFK”,“SFO”,“ATL”,“SFO”]
解释：另一种有效的行程是 [“JFK”,“SFO”,“ATL”,“JFK”,“ATL”,“SFO”] ，但是它字典排序更大更靠后。

提示

  • 1 <= tickets.length <= 300
  • tickets[i].length == 2
  • fromi.length == 3
  • toi.length == 3
  • fromi 和 toi 由大写英文字母组成
  • fromi != toi

代码解析

回溯遍历（超时）

回溯遍历每一种可能
当出现第一种可能的路线，之间加入。
当出现新的可能路线，与老路线对比，如果字典排序小于，则替换老路线

class Solution {
public:vector<string> resul;vector<string> path;void backtraking(vector<vector<string>>& tickets , string Indnx ,  vector<bool> &used){//找到路线，看是否替换老的路径//如果没有老路径直接加入，如果相同就返回，如果不同路径按照字典比较if(path.size()==tickets.size()+1){if(resul.empty()==1) {resul = path;return;}else if(resul == path) return;else {for(int j=0 ;j<path.size();j++){for(int k=0 ;k<3;k++){if(resul[j][k] == path[j][k]) continue;else if(resul[j][k] < path[j][k])return;else if(resul[j][k] > path[j][k]) {resul.clear();resul = path;return;}}}}// cout<<"resu: ";// for(auto i:resul) cout<<i<<' ';// cout<<endl;return;}for(int i=0 ; i<tickets.size();i++){//如果当前机票使用过，或者当前机票目的地不对，跳过if(used[i]==true || tickets[i][0] != Indnx) continue;//如果当前机票可用，则加入路径if(used[i]== false && tickets[i][0] == Indnx){used[i] = true;path.push_back(tickets[i][1]);//递归，确定递归找的新机票。下一站机票的开始机场，就是当前机票的目的地机场backtraking(tickets,tickets[i][1],used);used[i] = false;path.pop_back();}}return;}vector<string> findItinerary(vector<vector<string>>& tickets) {vector<bool> used(tickets.size(),false);path.push_back("JFK");backtraking(tickets,"JFK",used);return resul;}
};
排序再回溯

先对输入票排序，其中排序按照票的目的地的字典减少排序（因为出发点是确定的，目的地多种找最优解）
之后回溯遍历找路线，发现的第一个路线即为最优路线

class Solution {
public://按飞机票目的地（字符串vector第二个参数）字典减小排序class compare{public:bool operator()( const vector<string> tickets1 ,const  vector<string> tickets2 ){if((tickets1[1])[0]  < (tickets2[1])[0]) return 1;else if((tickets1[1])[0]  == (tickets2[1])[0]){if((tickets1[1])[1]  < (tickets2[1])[1]) return 1;else if((tickets1[1])[1]  == (tickets2[1])[1]){if((tickets1[1])[2]  < (tickets2[1])[2]) return 1;else return 0;}return 0;}return 0;}};vector<string> resul;vector<string> path;bool find = false;void backtraking(vector<vector<string>>& tickets , string Indnx ,  vector<bool> &used){//找到一个路径就不找了，直接是最优路径if(find == true ) return;if(path.size()==tickets.size()+1){resul = path;find =true;return;}for(int i=0 ; i<tickets.size();i++){if(used[i]==true || tickets[i][0] != Indnx) continue;if(used[i]== false && tickets[i][0] == Indnx){used[i] = true;path.push_back(tickets[i][1]);backtraking(tickets,tickets[i][1],used);used[i] = false;path.pop_back();}}return;}vector<string> findItinerary(vector<vector<string>>& tickets) {vector<bool> used(tickets.size(),false);sort(tickets.begin(),tickets.end(),compare());// for(auto i:tickets) // {//      cout<<'[';//     for(auto j:i)//     {//          cout<<j<<' ';//     }//      cout<<']';// }path.push_back("JFK");backtraking(tickets,"JFK",used);return resul;}
};

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.mzph.cn/news/682961.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

2024龙年特别篇 -- 魔法指针 之 指针变量的意义 指针运算

2024龙年特别篇 -- 魔法指针 之 指针变量的意义 指针运算

学习完指针变量&#xff1a;链接后&#xff0c; 我们继续学习指针变量的应用 目录 程序展示 原始方式 指针变量方式 代码对比 指针运算 指针-整数 用指针打印数组内容 使用指针打印1-10中的奇数 指针-指针 指针的关系运算 程序展示 打印一个有10个元素的数组&am…
阅读更多...
语言与科技创新（大语言模型对科技创新的影响）

语言与科技创新（大语言模型对科技创新的影响）

1.科技创新中的语言因素 科技创新中的语言因素至关重要&#xff0c;具体体现在以下几个方面&#xff1a; 科技文献交流&#xff1a; 英语作为全球科学研究的通用语言&#xff0c;极大地推动了科技成果的国际传播与合作。科学家们在发表论文、报告研究成果时&#xff0c;大多选…
阅读更多...
ChatGPT高效提问—prompt实践（教师助手）

ChatGPT高效提问—prompt实践（教师助手）

ChatGPT高效提问—prompt实践&#xff08;教师助手&#xff09; 下面来看看ChatGPT在教育领域有什么用途。 首先设定ChatGPT的角色为高中教师助手。 输入prompt: ChatGPT输出&#xff1a; ​ 教师助手的角色已经设置完成。下面通过几种不同的情景演示如何使用。 1.1.1 制定…
阅读更多...
2001-2022年368个地级市平均气温数据

2001-2022年368个地级市平均气温数据

2001-2022年368个地级市平均气温数据 1、时间:2001-2022年 2、范围&#xff1a;368个地级市 3、来源&#xff1a;基于NOAA下属NCEI提供的原始数据编制而成的。 4、指标&#xff1a;年份、省份、省份代码、城市、城市代码、平均气温 5、指标解释&#xff1a;平均气温指某一…
阅读更多...
【JavaEE】_JavaScript（Web API）

【JavaEE】_JavaScript（Web API）

目录 1. DOM 1.1 DOM基本概念 1.2 DOM树 2. 选中页面元素 2.1 querySelector 2.2 querySelectorAll 3. 事件 3.1 基本概念 3.2 事件的三要素 3.3 示例 4.操作元素 4.1 获取/修改元素内容 4.2 获取/修改元素属性 4.3 获取/修改表单元素属性 4.3.1 value&#xf…
阅读更多...
机器学习、深度学习、强化学习、迁移学习的关联与区别

机器学习、深度学习、强化学习、迁移学习的关联与区别

Hi&#xff0c;大家好&#xff0c;我是半亩花海。本文主要了解并初步探究机器学习、深度学习、强化学习、迁移学习的关系与区别&#xff0c;通过清晰直观的关系图展现出四种“学习”之间的关系。虽然这四种“学习”方法在理论和应用上存在着一定的区别&#xff0c;但它们之间也…
阅读更多...
FreeRTOS 队列管理

FreeRTOS 队列管理

概览 基于 FreeRTOS 的应用程序由一组独立的任务构成——每个任务都是具有独立权 限的小程序。这些独立的任务之间很可能会通过相互通信以提供有用的系统功能。 FreeRTOS 中所有的通信与同步机制都是基于队列实现的。 本章期望让读者了解以下事情 　 如何创建一个队列 　 …
阅读更多...
有限合伙协议书（模板）下

有限合伙协议书（模板）下

第六章 合伙事务的执行 第十七条 有限合伙人不执行合伙事务&#xff0c;对外不具有代表权。有限合伙企业由普通合伙人执行合伙事务。 第十八条 经全体合伙人一致同意可以委托一个普通合伙人&#xff08;也可以委托数个普通合伙人&#xff09;对外代表合伙企业&#xff0c;执…
阅读更多...
算法学习——LeetCode力扣回溯篇1

算法学习——LeetCode力扣回溯篇1

算法学习——LeetCode力扣回溯篇1 77. 组合 77. 组合 - 力扣&#xff08;LeetCode&#xff09; 描述 任何顺序 返回答案。 示例 示例 1&#xff1a; 输入&#xff1a;n 4, k 2 输出&#xff1a; [ [2,4], [3,4], [2,3], [1,2], [1,3], [1,4], ] 示例 2&#xff1a; 输…
阅读更多...
【机器学习案例4】为机器学习算法编码分类数据【含源码】

【机器学习案例4】为机器学习算法编码分类数据【含源码】

目录 编码分类数据 序数编码 标签编码 一次性编码 目标编码 目标编码的优点 目标编码的缺点 在现实生活中，收集的原始数据很少采用我们可以直接用于机器学习模型的格式，即数值型数据。因此，需要进行一些预处理，以便以正确的格式呈现数据、选择信息丰富的数据或降低其…
阅读更多...
【C++函数探幽】内联函数inline

【C++函数探幽】内联函数inline

&#x1f4d9; 作者简介 &#xff1a;RO-BERRY &#x1f4d7; 学习方向&#xff1a;致力于C、C、数据结构、TCP/IP、数据库等等一系列知识 &#x1f4d2; 日后方向 : 偏向于CPP开发以及大数据方向&#xff0c;欢迎各位关注&#xff0c;谢谢各位的支持 目录 1. 前言2.概念3.特性…
阅读更多...
GPT-4带来的思想火花

GPT-4带来的思想火花

GPT-4能够以其强大的生成能力和广泛的知识储备激发出众多思想火花。它能够在不同的情境下生成新颖的观点、独特的见解和富有创意的解决方案&#xff0c;这不仅有助于用户突破思维定势&#xff0c;还能促进知识与信息在不同领域的交叉融合。 对于研究者而言&#xff0c;GPT-4可能…
阅读更多...
浅谈业务场景中缓存的使用

浅谈业务场景中缓存的使用

业务场景中缓存的使用 一、背景二、缓存分类1.本地缓存2.分布式缓存 三、缓存读写模式1.读请求2.写请求 四、缓存穿透1.缓存空对象2.请求校验3.请求来源限制4.布隆过滤器 五、缓存击穿1.改变过期时间2.串行访问数据库 六、缓存雪崩1.避免集中过期2.提前更新缓存 七、缓存与数据…
阅读更多...
【MATLAB】鲸鱼算法优化混合核极限学习机(WOA-HKELM)回归预测算法

【MATLAB】鲸鱼算法优化混合核极限学习机(WOA-HKELM)回归预测算法

有意向获取代码&#xff0c;请转文末观看代码获取方式~也可转原文链接获取~ 1 基本定义 鲸鱼算法优化混合核极限学习机&#xff08;WOA-HKELM&#xff09;回归预测算法是一种结合鲸鱼优化算法和混合核极限学习机的混合算法。其原理主要包含以下几个步骤&#xff1a; 初始化&am…
阅读更多...
UniApp学习之旅：从入门到快速上手

UniApp学习之旅：从入门到快速上手

随着移动互联网的迅猛发展&#xff0c;跨平台应用开发成为了开发者们的热门选择。UniApp&#xff0c;作为一款使用Vue.js开发所有前端应用的框架&#xff0c;因其简单、高效、易上手的特性&#xff0c;受到了广大开发者的青睐。本文将带你走进UniApp的世界&#xff0c;从基础学…
阅读更多...
【leetcode】深搜、暴搜、回溯、剪枝（C++）2

【leetcode】深搜、暴搜、回溯、剪枝（C++）2

深搜、暴搜、回溯、剪枝&#xff08;C&#xff09;2 一、括号生成1、题目描述2、代码3、解析 二、组合1、题目描述2、代码3、解析 三、目标和1、题目描述2、代码3、解析 四、组合总和1、题目描述2、代码3、解析 五、字母大小写全排列1、题目描述2、代码3、解析 六、优美的排列1…
阅读更多...
鸿蒙视频播放器，主要包括视频获取和视频播放功能：

鸿蒙视频播放器，主要包括视频获取和视频播放功能：

鸿蒙视频播放器&#xff0c;主要包括视频获取和视频播放功能&#xff1a; 1 获取本地视频或者网络视频。 2 通过media.createAVPlayer创建播放器AVPlayer&#xff0c;然后进行视频播放。 3 通过VideoController进行AVPlayerState的状态管理&#xff0c;如开始&#xff0c;停止&…
阅读更多...
2.15 字符串练习

2.15 字符串练习

1、选择题 1.1、有以下程序 int main() { char a[7]"a0\0a0\0";int i,j; isizeof(a); jstrlen(a); printf("%d %d\n",i,j); } //strlen求出字符串的长度&#xff0c;其实是字符串中字符的个数&#xff0c;不包括\0 程序运行后的输出结果是 C…
阅读更多...
K210开发环境搭建（VS Code）

K210开发环境搭建（VS Code）

一、新建一个文件夹&#xff0c;就叫K210 二、再K210文件夹里面再新建一个文件夹&#xff0c;就叫CMake 三、找到官方提供的资料包里的cmake安装包&#xff0c; 或者直接去cmake官方下载网址进行下载 CMake官方下载网址&#xff1a;https://cmake.org/download/ 四、双击安装…
阅读更多...
Screw自动生成数据库文档

Screw自动生成数据库文档

Screw简介 官方地址 Screw可以根据数据库中的表自动生成HTML、Word、Markdown格式的文档。 Springboot 3.1集成 生成Springboot项目 Spring Initializr Maven依赖 <dependency><groupId>cn.smallbun.screw</groupId><artifactId>screw-core</…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023