傅立叶变换的本质
离散傅立叶变换的本质就是用一系列的正弦(或者余弦)函数的和来拟合一个周期函数f(t)。公式如下:
(1)
其中T是f(t)的周期,即f(t+T)=f(t)对任意t成立。和
的周期是
。换句话说,后两者的频率是f(t)的频率的k倍。这说明,我们在拟合任意一个周期函数时,只需要考虑整数倍频率的三角函数,而不需要考虑任意倍数的三角函数。
更进一步,我们能不能在正弦和余弦之间只保留一个呢?还真行,因为:
(2)
其中,
。值得注意的是,这个转换在
或
等于0或者都等于0时仍然成立。
因此,我们只需要正弦函数就能够拟合任意周期函数。其中参数和
分别被称为正弦函数的振幅和偏移。也就是说,虽然三角函数少了一个,但参数数量并没有增加。
类似地,我们可以很容易地把公式(2)转换为一个具有振幅和偏移的余弦函数。我们把这两种变换分别称为正弦傅立叶变换和余弦傅立叶变换。
正弦和余弦傅立叶变换意味着什么
再来看看下面两个公式,告诉我,你会想到什么?
(3)
(4)
没错,我们会想到点的极坐标。就是旋转半径的长度,
是旋转时间。
是角速度,是一个常量。
则是旋转起始角度。公式(3)和(4)可以用来分别计算直角坐标系下点的横坐标和纵坐标。
总结一下,我们得到以下两个公式:
(5)
(6)
其中函数和
分别用来计算点的横、纵坐标。
的取值范围是[0, T]。
应用
公式(5)和(6)提示我们:直角坐标系下,在一幅由一定顺序的点组成的图像中,每个点的横、纵坐标可以分开来计算,互不干扰。并且,每一个这样的坐标——不管是横坐标还是纵坐标——都可以转化为一组固定的半径和起始角度的组合,即和
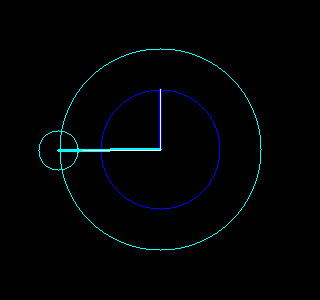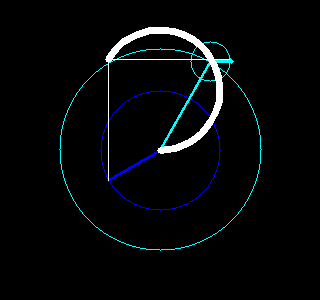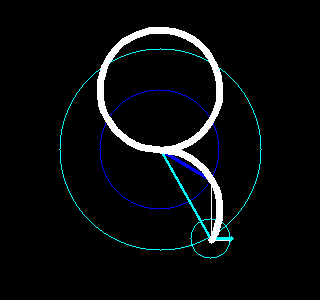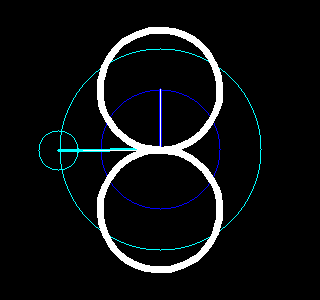
。每一对半径和起始角度又对应了一个以整数倍频率旋转着的圆。把这些圆的圆心按频率从低到高首尾相连,就可以构成一幅有趣的动画,该动画不仅重现了原图像,更揭示了傅立叶变换的本质。
根据这个想法,我们用Python写了一些程序,利用快速傅立叶变换(参见函数numpy.fft.fft)、OpenCV(参见包cv2)和图像io(参见包imageio)实现了一些有趣的动画,能够绘画出我们事先指定的图像。结果如下。
|
|
|
 | 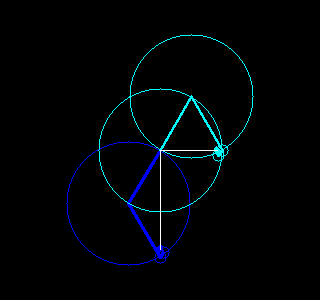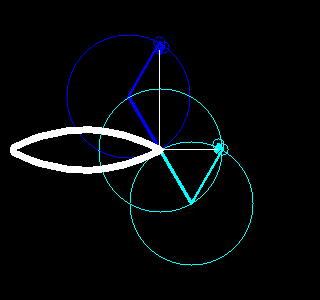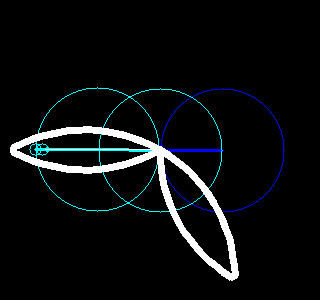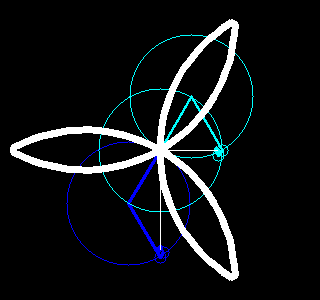 |
 | 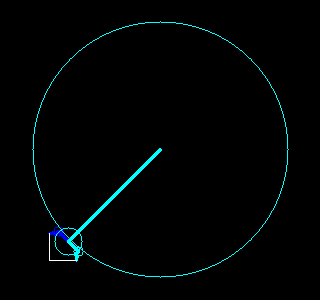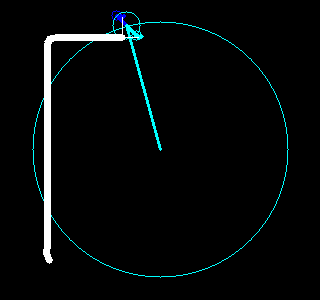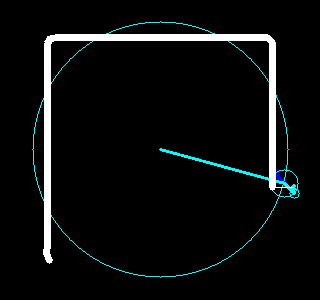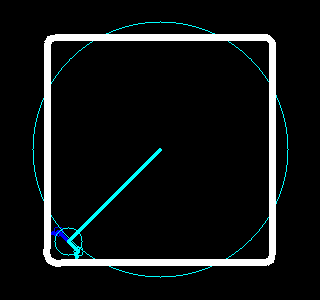 |
甚至可以绘画0~9十个数字。
 | 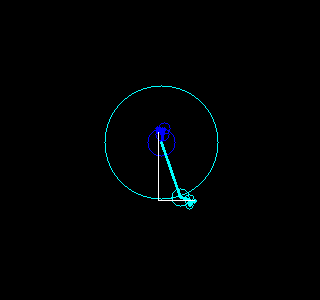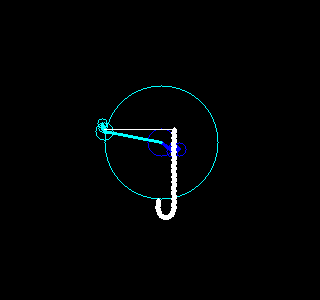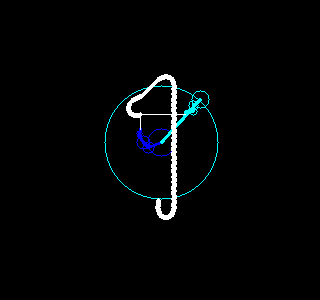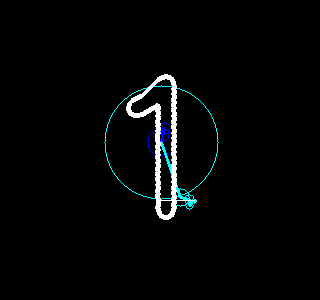 |  |
 |  |  |
 |  |  |
 |
最后给大家看的是奥运五环:







导数与微分)


)








:JIT即时编译器原理)
