本专题主要介绍容斥原理。
大家高中的时候肯定接触过韦恩图,容斥原理比较通俗的理解就是减去所有可能并加上重叠的部分。
我们直接看公式:
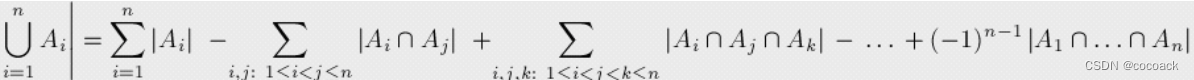
知道后,我们先看道模板题:
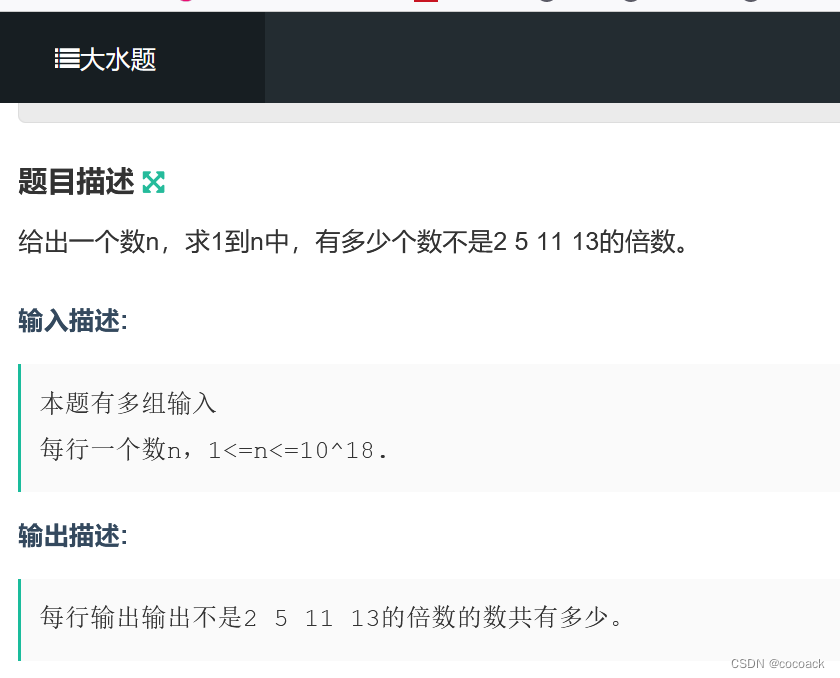
下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
#define int long long
int a[6],n;
signed main(){a[0]=2;a[1]=5;a[2]=11;a[3]=13;while(cin>>n){int sum=0;for(int i=0;i<=(1<<4)-1;i++){int cnt=0;int ww=1;for(int j=0;j<4;j++){if((i>>j)&1==1){ww*=a[j];cnt++;}}if(cnt%2==0) sum+=n/ww;else sum-=n/ww;}printf("%lld\n",sum);}
}接下来看一道有趣的题:

下面是分析:
首先,题目应该改为被1只及以上。同时10^4,显然不能容斥原理,但我们可以借鉴它先减后弥补的思想。
下面是解法(十分的巧妙):


下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
#define int long long
int n,m,x;
map<int,int> mp;
int gcd(int a,int b){while(b){int tmp=b;b=a%b;a=tmp;}return a;
}
signed main(){scanf("%lld%lld",&n,&m);for(int i=1;i*i<=m;i++){if(m%i==0){mp[i]=0;mp[m/i]=0;}}mp.erase(m);for(int i=1;i<=n;i++){scanf("%lld",&x);int yy=gcd(x,m);for(map<int,int>::iterator it=mp.begin();it!=mp.end();it++){if((it->first)%yy==0) mp[it->first]=1;}}int sum=0;for(map<int,int>::iterator it=mp.begin();it!=mp.end();it++){if(it->second==0) continue;int num=m/(it->first);sum+=((it->first)*(num))*(num-1)/2*(it->second);for(map<int,int>::iterator it1=it;it1!=mp.end();it1++){if(it1==it) it1++;if(it1==mp.end()) break;if((it1->first)%(it->first)==0) mp[it1->first]-=it->second;}}cout<<sum;
}(2024))



项目方舟框架(ArkUI)之ImageAnimator组件)


)

)




C. Kefa and Park(DFS、实现))



 C. Choose the Different Ones(Java))
![[Doris] Doris的安装和部署 (二)](http://pic.xiahunao.cn/[Doris] Doris的安装和部署 (二))