主要是点(point)、线(linestring)、面(surface)
1 基本方法和属性
object.area | 返回对象的面积(浮点数) |
object.bounds | 返回一个(minx, miny, maxx, maxy)元组(浮点值),该元组界定了对象的边界 |
object.length | 返回对象的长度(浮点数) |
object.minimum_clearance | 返回通过移动一个节点所能产生的无效几何形状的最小距离 这可以被视为几何形状的稳健性的度量,其中较大的最小清晰度值表示更稳健的几何形状。 如果一个几何形状不存在最小清晰度,例如一个点,这将返回math.infinity。
|
object.geom_type | 返回一个字符串,指定对象的几何类
|
object.distance | 返回到另一个几何对象的最小距离(浮点数)
|
object.hausdorff_distance | 返回到另一个几何对象的豪斯多夫距离(浮点数)。 两个几何形状之间的豪斯多夫距离是一个几何形状上的点到另一个几何形状上最近点的最远距离
|
object.representative_point |
|
2 Points
2.1 创建点
使用 Shapely 创建点时,可以直接提供 x 和 y 的坐标值,或者提供一个包含 x 和 y 值的元组
from shapely import Point# 使用位置坐标值创建点
point = Point(0.0, 0.0)# 使用点元组参数创建点
q = Point((0.0, 0.0))
2.2 属性和方法
point.area | 始终是0 |
point.length | 始终是0 |
point.bounds | 对于点来说,这些值是点的坐标
|
| 访问坐标值
coords还可以这样使用:
|
3 LineStrings
- 接受一个有序的2个或更多个 (x, y[, z]) 点元组序列
- 构造出的
LineString对象代表点之间的一个或多个连接的线性样条。有序序列中允许重复的点,但可能会导致性能损失,应该避免。LineString可以自我交叉

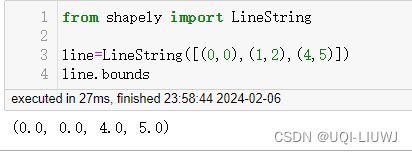
3.1 方法和属性
line.area | 始终是0 |
line.length | 线段的长度 |
line.bounds | x-y 边界框是一个 (minx, miny, maxx, maxy) 元组
|
line.coords | 定义的坐标值可以通过
|
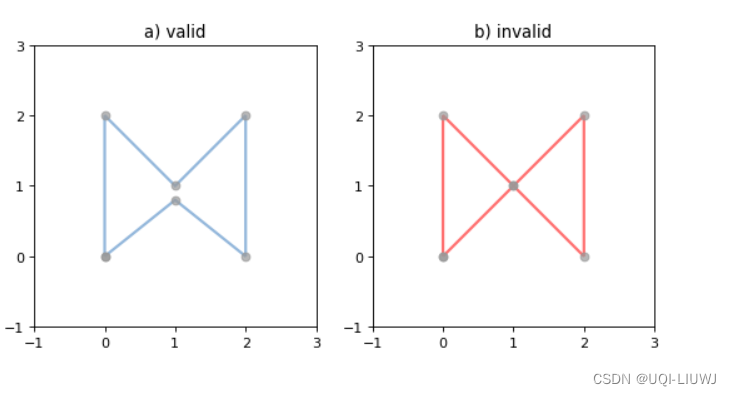
4 LinearRing
- 受一个有序的 (x, y[, z]) 点元组序列
- 序列可以通过在第一个和最后一个索引处传递相同的值来显式关闭。否则,序列将通过将第一个元组复制到最后一个索引来隐式关闭
LinearRing有零面积和非零长度- 与
LineString一样,有序序列中允许重复的点,但可能会导致性能损失,应该避免。LinearRing不能自我交叉,也不能在单个点上接触自身
coords |  |
area | 始终为0 |
length | 长度 |
bounds |
5 polygon
Polygon类的构造函数接受两个位置参数。- 第一个参数是一个有序的 (x, y[, z]) 点元组序列,这与
LinearRing的情况完全相同。 - 第二个参数是一个可选的,无序的环状序列序列,指定了特征的内部边界或“洞”(同时在第一个LinearRing里面的部分挖掉,不在第一个
- 第一个参数是一个有序的 (x, y[, z]) 点元组序列,这与
from shapely import Polygonpoly=Polygon([(0,2),(2,2),(2,0)],[[(0.5, 1.5), (1.5, 1.5), (1.5, 0.5), (0.5, 0.5)]])
poly
area | 面积 |
length | |
bounds | |
exteriorinteriors | 访问组成环(外环 内环)
|
6 box
方形多边形
from shapely.geometry import boxbox(0,0,1,2)
7 形状的集合
7.1 GeometryCollection
- 当两个几何对象的交集包含多种类型的几何元素时,例如
LineString和Point,Shapely 会使用GeometryCollection类型来表示这些结果
from shapely.geometry import LineStringa = LineString([(0, 0), (1, 1), (1,2), (2,2)])
b = LineString([(0, 0), (1, 1), (2,1), (2,2)])
x = a.intersection(b)
print(x)
#GEOMETRYCOLLECTION (LINESTRING (0 0, 1 1), POINT (2 2))
7.1.1 geoms
通过 geoms 属性访问 GeometryCollection 中的成员
list(x.geoms)
#[<LINESTRING (0 0, 1 1)>, <POINT (2 2)>]7.2 集合中的点:MultiPoint 类
MultiPoint 类用于表示点的集合。
构造函数接受一个点的序列,其中每个点可以是 (x, y[, z]) 形式的元组。
from shapely import MultiPoint
points = MultiPoint([(0.0, 0.0), (1.0, 1.0)])
print(points.area)
# 输出 0.0
print(points.length)
# 输出 0.0
area | 始终为0 |
length | 始终为0 |
bounds | |
geoms | MultiPoint中的点
|
7.3 集合中的线:MultiLineString 类
MultiLineString 类表示线的集合。构造函数接受一系列类似线的序列或对象。
一个 MultiLineString 对象的面积为零,长度为非零

from shapely import MultiLineString
coords = [((0, 0), (1, 1)), ((-1, 0), (1, 0))]
lines = MultiLineString(coords)
lines
area | 始终为0 |
length | |
bounds | |
geoms | MultiLineString中的点
|
7.4 多边形中的点 MultiPolygon
from shapely import Polygon
from shapely import MultiPolygon
polygon1 = Polygon([(0, 0), (1, 1), (1, 0),(0,1)])
polygon2 = Polygon([(0,0),(0,2),(1,1)])multiPolygon=MultiPolygon([polygon1,polygon2])
multiPolygon
area | |
length | |
bounds | |
geoms |  |














明朝事儿》)









)




)
)
