视觉SLAM十四讲学习笔记（二）三维空间刚体

哔哩哔哩课程连接：视觉SLAM十四讲ch3_哔哩哔哩_bilibili

一、旋转矩阵

1 点、向量、坐标系

2 坐标系间的欧氏变换

3 变换矩阵与齐次坐标

二、实践：Eigen（1）

运行报错记录与解决

三、旋转向量和欧拉角

1 旋转向量

2 欧拉角

四、四元数

1 四元数的定义

2 四元数的运算

3 用四元数表示旋转

4 四元数到旋转矩阵的转换

五、实践：Eigen（2）

useGeometry

visualizeGeometry

总结

前言

问题用两个方程描述：

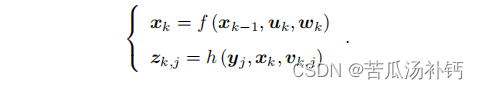
本文将介绍视觉 SLAM 的基本问题之一：一个刚体在三维空间中的运动是如何描述的。

将介绍旋转矩阵、四元数、欧拉角的意义，以及它们是如何运算和转换的。在实践部分，将介绍线性代数库 Eigen。它提供了 C++ 中的矩阵运算，并且它的 Geometry 模块还提供了四元数等刚体运动的描述。Eigen 的优化非常完善，但是它的使用方法有一些特殊的地方。

一、旋转矩阵

1 点、向量、坐标系

三维空间由三个轴组成，所以一个空间点的位置可以由三个坐标指定。不过，刚体不光有位置，还有自身的姿态。相机也可以看成三维空间的刚体，于是位置是指相机在空间中的哪个地方，而姿态则是指相机的朝向。

点

点存在于三维空间之中
点和点可以组成向量
点本身由原点指向它的向量所描述

向量

带指向性的箭头
可以进行加法、减法等运算

坐标系：由三个正交的拍组成

构成线性空问的一组基
左手系和右手系

定义坐标系后、向量可以由坐标表示，如果我们确定一个坐标系，也就是一个线性空间的基 (e1, e2, e3)，那就可以谈论向量 a 在这组基下的坐标了：

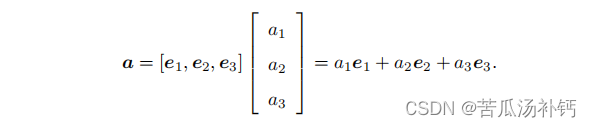
向量的运算可以由坐标运算来表达，内积（可以描述向量间的投影关系）可以写成：

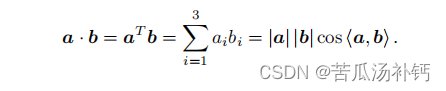
外积，外积的方向垂直于这两个向量，大小为 |a| |b|sin <a, b>，是两个向量张成的四边形的有向面积：

引入了 ∧ 符号，把 a 写成一个矩阵。事实上是一个反对称矩阵(Skew-symmetric)，你可以将 ∧ 记成一个反对称符号。外积只对三维向量存在定义，还能用外积表示向量的旋转。

2 坐标系间的欧氏变换

在SLAM中：

固定的世界坐标系和移动的机器人坐标系
机器人坐标系随着机器人运动而改变，每个时刻都有新的坐标系

描述两个坐标系之间的旋转关系，再加上平移，统称为坐标系之间的变换关系。

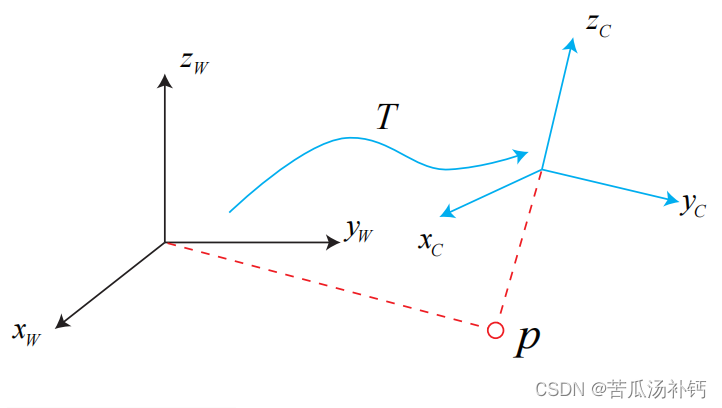
上图为坐标变换。对于同一个向量 p，它在世界坐标系下的坐标 pw 和在相机坐标系下的 pc 是不同的。这个变换关系由坐标系间的变换矩阵 T 来描述。

相机运动是一个刚体运动，它保证了同一个向量在各个坐标系下的长度和夹角都不会发生变化。这种变换称为欧氏变换。

设某个单位正交基 (e1, e2, e3) 经过一次旋转，变成了 (e ′ 1 , e ′ 2 , e ′ 3 )。那么，对于同一个向量 a（注意该向量并没有随着坐标系的旋转而发生运动），它在两个坐标系下的坐标为 [a1, a2, a3] T 和 [a ′ 1 , a ′ 2 , a ′ 3 ] T。根据坐标的定义，有：

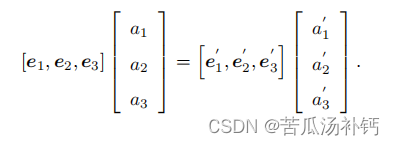
对上面等式左右同时左乘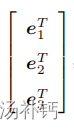，那么左边的系数变成了单位矩阵，所以：

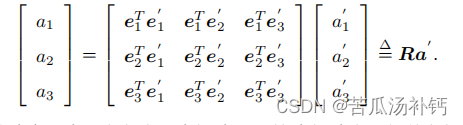
把中间的阵定义成一个矩阵 R。这个矩阵由两组基之间的内积组成，刻画了旋转前后同一个向量的坐标变换关系。只要旋转是一样，那么这个矩阵也一样。矩阵 R 描述了旋转本身，因此又称为旋转矩阵，有以下性质：

行列式为1
正交阵
对于同一个旋转变化，对应唯一的旋转矩阵
旋转矩阵的充要条件：行列式为 1 的正交矩阵
集合定义：SO(n) 是特殊正交群（Special Orthogonal Group）。

旋转矩阵可以描述相机的旋转。由于旋转矩阵为正交阵，它的逆（即转置）描述了一个相反的旋转。

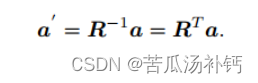
考虑平移，设平移向量为 t ，旋转矩阵为 R ，则

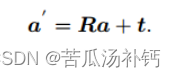
3 变换矩阵与齐次坐标

齐次坐标：齐次坐标是用N+1个数来表示N维坐标的一种方式。

变换矩阵（Transform Matrix）：如果T是一个把Rn映射到Rm的线性变换，且x是一个具有n个元素的列向量，那么我们把m×n的矩阵A，称为T的变换矩阵。

假设进行了两次变换：R1, t1 和 R2, t2，满足：

b = R1a + t1
c = R2b + t2

但是从 a 到 c 的变换为： c = R2 (R1a + t1) + t2.

引入齐次坐标和变换矩阵重写：

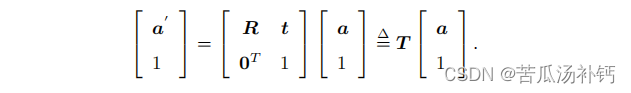
关于变换矩阵 T，它具有比较特别的结构：左上角为旋转矩阵，右侧为平移向量，左下角为 0 向量，右下角为 1。这种矩阵又称为特殊欧氏群（Special Euclidean Group）：

在不引起歧义的情况下，我们以后不区别齐次坐标与普通的坐标的符号，默认我们使用的是符合运算法则的那一种。

二、实践：Eigen（1）

本章需要虚拟机或ubuntu系统，自行安装。下载配套资源，记录在视觉SLAM十四讲学习笔记（一）初识SLAM-CSDN博客

打开文件夹ch3

Eigen安装：

sudo apt-get install libeigen3-dev

装好后可以ls查看头文件库

ls /usr/include/eigen3/

Eigen是一个纯用头文件搭建起来的库，没有源文件。这意味着只能找到它的头文件，而没有类似.so或.a的二进制文件。在使用时，只需引入Eigen的头文件即可，不需要链接库文件。

然后就可以在你的程序引用#include <Eigen/Core>。

cmake .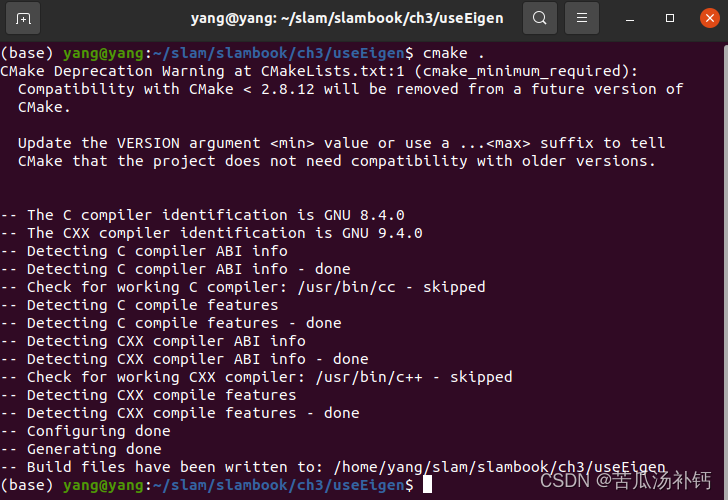

make

下面一段代码实际联系Eigen的使用：

#include <iostream>
using namespace std;
#include <ctime>
// Eigen 部分
#include <Eigen/Core>
// 稠密矩阵的代数运算（逆，特征值等）
#include <Eigen/Dense>#define MATRIX_SIZE 50/****************************
* 本程序演示了 Eigen 基本类型的使用
****************************/int main( int argc, char** argv )
{// Eigen 中所有向量和矩阵都是Eigen::Matrix，它是一个模板类。它的前三个参数为：数据类型，行，列// 声明一个2*3的float矩阵Eigen::Matrix<float, 2, 3> matrix_23;// 同时，Eigen 通过 typedef 提供了许多内置类型，不过底层仍是Eigen::Matrix// 例如 Vector3d 实质上是 Eigen::Matrix<double, 3, 1>，即三维向量Eigen::Vector3d v_3d;// 这是一样的Eigen::Matrix<float,3,1> vd_3d;// Matrix3d 实质上是 Eigen::Matrix<double, 3, 3>Eigen::Matrix3d matrix_33 = Eigen::Matrix3d::Zero(); //初始化为零// 如果不确定矩阵大小，可以使用动态大小的矩阵Eigen::Matrix< double, Eigen::Dynamic, Eigen::Dynamic > matrix_dynamic;// 更简单的Eigen::MatrixXd matrix_x;// 这种类型还有很多，我们不一一列举// 下面是对Eigen阵的操作// 输入数据（初始化）matrix_23 << 1, 2, 3, 4, 5, 6;// 输出cout << matrix_23 << endl;// 用()访问矩阵中的元素for (int i=0; i<2; i++) {for (int j=0; j<3; j++)cout<<matrix_23(i,j)<<"\t";cout<<endl;}// 矩阵和向量相乘（实际上仍是矩阵和矩阵）v_3d << 3, 2, 1;vd_3d << 4,5,6;// 但是在Eigen里你不能混合两种不同类型的矩阵，像这样是错的// Eigen::Matrix<double, 2, 1> result_wrong_type = matrix_23 * v_3d;// 应该显式转换Eigen::Matrix<double, 2, 1> result = matrix_23.cast<double>() * v_3d;cout << result << endl;Eigen::Matrix<float, 2, 1> result2 = matrix_23 * vd_3d;cout << result2 << endl;// 同样你不能搞错矩阵的维度// 试着取消下面的注释，看看Eigen会报什么错// Eigen::Matrix<double, 2, 3> result_wrong_dimension = matrix_23.cast<double>() * v_3d;// 一些矩阵运算// 四则运算就不演示了，直接用+-*/即可。matrix_33 = Eigen::Matrix3d::Random();      // 随机数矩阵cout << matrix_33 << endl << endl;cout << matrix_33.transpose() << endl;      // 转置cout << matrix_33.sum() << endl;            // 各元素和cout << matrix_33.trace() << endl;          // 迹cout << 10*matrix_33 << endl;               // 数乘cout << matrix_33.inverse() << endl;        // 逆cout << matrix_33.determinant() << endl;    // 行列式// 特征值// 实对称矩阵可以保证对角化成功Eigen::SelfAdjointEigenSolver<Eigen::Matrix3d> eigen_solver ( matrix_33.transpose()*matrix_33 );cout << "Eigen values = \n" << eigen_solver.eigenvalues() << endl;cout << "Eigen vectors = \n" << eigen_solver.eigenvectors() << endl;// 解方程// 我们求解 matrix_NN * x = v_Nd 这个方程// N的大小在前边的宏里定义，它由随机数生成// 直接求逆自然是最直接的，但是求逆运算量大Eigen::Matrix< double, MATRIX_SIZE, MATRIX_SIZE > matrix_NN;matrix_NN = Eigen::MatrixXd::Random( MATRIX_SIZE, MATRIX_SIZE );Eigen::Matrix< double, MATRIX_SIZE,  1> v_Nd;v_Nd = Eigen::MatrixXd::Random( MATRIX_SIZE,1 );clock_t time_stt = clock(); // 计时// 直接求逆Eigen::Matrix<double,MATRIX_SIZE,1> x = matrix_NN.inverse()*v_Nd;cout <<"time use in normal inverse is " << 1000* (clock() - time_stt)/(double)CLOCKS_PER_SEC << "ms"<< endl;// 通常用矩阵分解来求，例如QR分解，速度会快很多time_stt = clock();x = matrix_NN.colPivHouseholderQr().solve(v_Nd);cout <<"time use in Qr decomposition is " <<1000*  (clock() - time_stt)/(double)CLOCKS_PER_SEC <<"ms" << endl;return 0;
}

运行报错记录与解决

在学习SlamBook2-ch3中对Eigen矩阵运算包内容时，编写好相关代码后make报错：

[ 50%] Building CXX object CMakeFiles/eigenMatrix.dir/eigenMatrix.cpp.o
/home/yang/slam/SLAMBook/ch3/useEigen/useEigen/src/eigenMatrix.cpp:6:10: fatal error: Eigen/Core: 没有那个文件或目录#include <Eigen/Core>^~~~~~~~~~~~
compilation terminated.
CMakeFiles/eigenMatrix.dir/build.make:62: recipe for target 'CMakeFiles/eigenMatrix.dir/eigenMatrix.cpp.o' failed
make[2]: *** [CMakeFiles/eigenMatrix.dir/eigenMatrix.cpp.o] Error 1
CMakeFiles/Makefile2:67: recipe for target 'CMakeFiles/eigenMatrix.dir/all' failed
make[1]: *** [CMakeFiles/eigenMatrix.dir/all] Error 2
Makefile:83: recipe for target 'all' failed
make: *** [all] Error 2

因为在当初安装eigen库时，系统默认安装到了 /usr/include/eigen3/Eigen 路径下，根据CmakeLists中的路径无法定位到Eigen库文件文件夹所在的位置，从而报错。

解决方法：
使用下面命令将eigen的安装路径映射到/usr/include路径下:

sudo ln -s /usr/include/eigen3/Eigen /usr/include/Eigen

三、旋转向量和欧拉角

1 旋转向量

矩阵表示方式至少有以下缺点：

SO(3) 的旋转矩阵有九个量，但一次旋转只有三个自由度。因此这种表达方式是冗余的。同理，变换矩阵用十六个量表达了六自由度的变换。
旋转矩阵自身带有约束：它必须是个正交矩阵，且行列式为 1。变换矩阵也是如此。当我们想要估计或优化一个旋转矩阵/变换矩阵时，这些约束会使得求解变得更困难。

对于坐标系的旋转，任意旋转都可以用一个旋转轴和一个旋转角来刻画。于是，我们可以使用一个向量，其方向与旋转轴一致，而长度等于旋转角。这种向量，称为旋转向量（或轴角，Axis-Angle）。这种表示法只需一个三维向量即可描述旋转。同样，对于变换矩阵，我们使用一个旋转向量和一个平移向量即可表达一次变换。这时的维数正好是六维。

角轴与旋转矩阵的不同：

旋转矩阵:九个量，有正交性约来和行列式值约束
角轴:三个量，没有约衷

注意它们只是表达方式的不同，但表达的东西可以是同一个。角轴也就是后面要介绍的李代数。

假设有一个旋转轴为 n，角度为 θ 的旋转，显然，它对应的旋转向量为 θn。由旋转向量到旋转矩阵的过程由罗德里格斯公式（Rodrigues’s Formula ）表明，由于推导过程比较复杂，本文不作描述，只给出转换的结果：

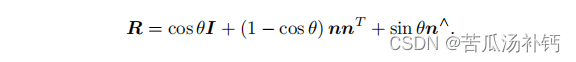
旋转矩阵转轴角：

角度：

轴：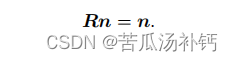

转轴 n 是矩阵 R 特征值 1 对应的特征向量。求解此方程，再归一化，就得到了旋转轴。

2 欧拉角

欧拉角提供了一种非常直观的方式来描述旋转——它使用了三个分离的转角，把一个旋转分解成三次绕不同轴的旋转。可以定义 ZY Z、ZY X 等等旋转方式。如果讨论更细一些，还需要区分每次旋转是绕固定轴旋转的，还是绕旋转之后的轴旋转的，这也会给出不一样的定义方式。

将腕转分解为三次不同轴上的转动,以便理解
例如:按Z-Y-X顺序转动
轴可以是定轴或动轴，顺序亦可不同,因此存在许多种定义方式不同的欧拉角
常见的有 yaw-pilch-roll(偏航-怕仰-滚转)角等等

ZY X 转角相当于把任意旋转分解成以下三个轴上的转角：

绕物体的 Z 轴旋转，得到偏航角 yaw；
绕旋转之后的 Y 轴旋转，得到俯仰角 pitch；
绕旋转之后的 X 轴旋转，得到滚转角 roll。

万向锁(Gimbal Lock)

ZYX顺序中，若Pitch为正负90度，则第三次旋转和第一次绕同一个轴，使得系统丢失了一个自由度――存在奇异性问题。

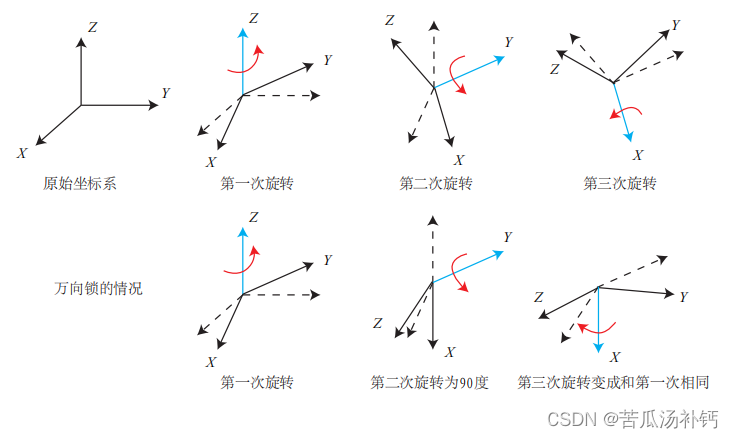
程序中直接使用欧拉角表达姿态，同样不会在滤波或优化中使用欧拉角表达旋转（因为它具有奇异性）。不过，若你想验证自己算法是否有错时，转换成欧拉角能够快速辨认结果的正确与否。

由于万向锁，欧拉角不适于插值和达代，往往只用于人机交互中。
可以证明,用三个实数来表达三维旋转时，会不可避免地碰到奇异性问题。
SLAM程序中很少直接使用欧拉角表达姿态

四、四元数

1 四元数的定义

四元数是 Hamilton 找到的一种扩展的复数，它既是紧凑的，也没有奇异性。一个四元数 q 拥有一个实部和三个虚部。本书把实部写在前面（也有地方把实部写在后面），像这样：

这里，s 称为四元数的实部，而 v 称为它的虚部。如果一个四元数虚部为 0，称之为实四元数。反之，若它的实部为 0，称之为虚四元数。

能用单位四元数表示三维空间中任意一个旋转，不过这种表达方式和复数有着微妙的不同。在复数中，乘以 i 意味着旋转 90 度。这是否意味着四元数中，乘 i 就是绕 i 轴旋转 90 度？那么，ij = k 是否意味着，先绕 i 转 90 度，再绕 j 转 90 度，就等于绕 k 转90 度？正确的事情应该是，乘以 i 应该对应着旋转 180 度，这样才能保证 ij = k 的性质。而 i 2 = −1，意味着绕i 轴旋转 360 度后，你得到了一个相反的东西。这个东西要旋转两周才会和它原先的样子相等。

假设某个旋转是绕单位向量 n = [nx, ny, nz] T 进行了角度为 θ 的旋转，那么这个旋转的四元数形式为：

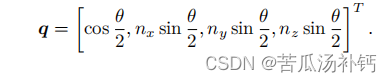
反之，亦可从单位四元数中计算出对应旋转轴与夹角：

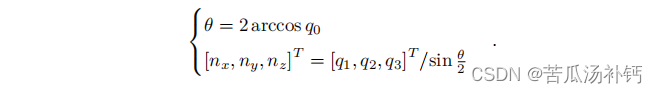
在四元数中，任意的旋转都可以由两个互为相反数的四元数表示。同理，取 θ 为 0，则得到一个没有任何旋转的实四元数：

2 四元数的运算

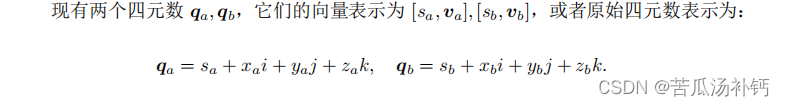
那么，它们的运算可表示如下。

加减法

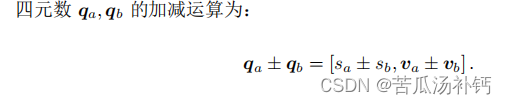
乘法：

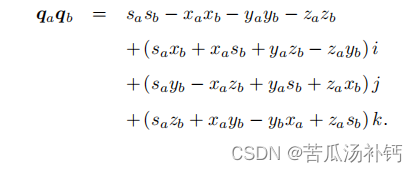
如果写成向量形式并利用内外积运算，乘法表达会更加简洁：

在该乘法定义下，两个实的四元数乘积仍是实的，这与复数也是一致的。然而，注意到，由于最后一项外积的存在，四元数乘法通常是不可交换的，除非 va 和 vb 在 R 3中共线，那么外积项为零。

共轭：

模长：

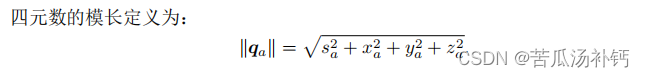
可以验证，两个四元数乘积的模即为模的乘积。这保证单位四元数相乘后仍是单位四元数。

逆：

如果 q 为单位四元数，逆和共轭就是同一个量。同时，乘积的逆有和矩阵相似的性质：

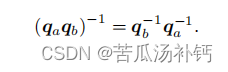
数乘与点乘：

3 用四元数表示旋转

这相当于把四元数的三个虚部与空间中的三个轴相对应。然后，用四元数 q 表示旋转：

可以验证，计算结果的实部为 0，故为纯虚四元数。其虚部的三个分量表示旋转后 3D 点的坐标。

4 四元数到旋转矩阵的转换

把四元数转换为矩阵的最直观方法，是先把四元数 q 转换为轴角 θ 和 n，然后再根据罗德里格斯公式转换为矩阵。

反之，由旋转矩阵到四元数的转换如下。假设矩阵为 R = {mij}, i, j ∈ [1, 2, 3]，其对应的四元数 q 由下式给出：

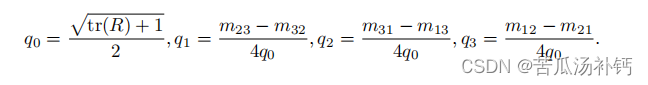
值得一提的是，由于 q 和 −q 表示同一个旋转，事实上一个 R 对应的四元数表示并不是惟一的。同时，除了上面给出的转换方式之外，还存在其他几种计算方法。实际编程中，当 q0 接近 0 时，其余三个分量会非常大，导致解不稳定，此时再考虑使用其他的方式进行转换。

五、实践：Eigen（2）

useGeometry

打开文件夹useGeometry，步骤和二、实践：Eigen（1） 一致

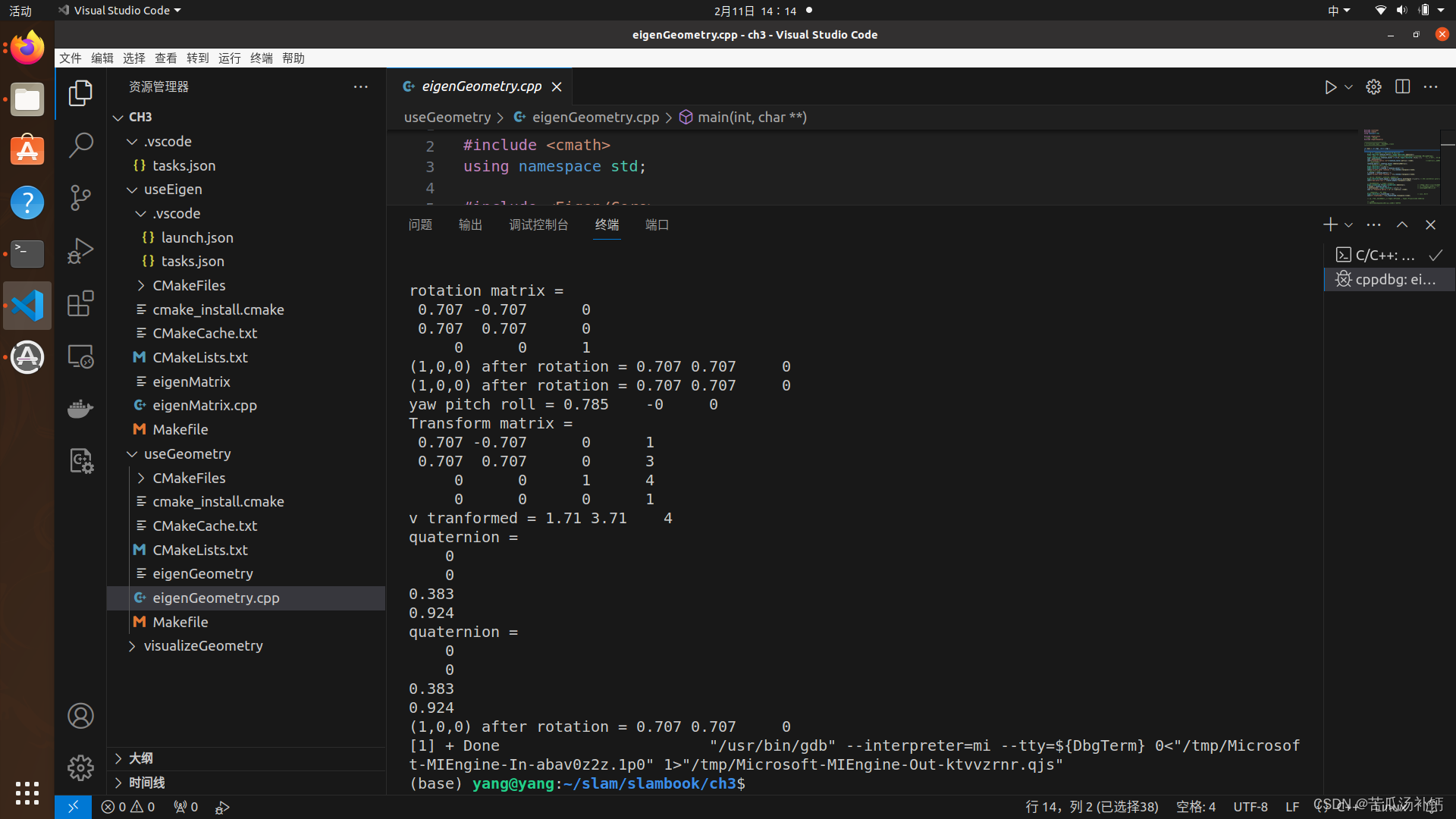
visualizeGeometry

打开文件夹visualizeGeometry，打开Readme.txt，文件内容如下：

1. How to compile this program:* use pangolin: slambook/3rdpart/Pangolin or download it from github: https://github.com/stevenlovegrove/Pangolin* install dependency for pangolin (mainly the OpenGL): 
sudo apt-get install libglew-dev* compile and install pangolin
cd [path-to-pangolin]
mkdir build
cd build
cmake ..
make 
sudo make install * compile this program:
mkdir build
cd build
cmake ..
make * run the build/visualizeGeometry2. How to use this program:The UI in the left panel displays different representations of T_w_c ( camera to world ). It shows the rotation matrix, tranlsation vector, euler angles (in roll-pitch-yaw order) and the quaternion.
Drag your left mouse button to move the camera, right button to rotate it around the box, center button to rotate the camera itself, and press both left and right button to roll the view. 
Note that in this program the original X axis is right (red line), Y is up (green line) and Z in back axis (blue line). You (camera) are looking at (0,0,0) standing on (3,3,3) at first. 3. Problems may happen:
* I found that in virtual machines there may be an error in pangolin, which was solved in its issue: https://github.com/stevenlovegrove/Pangolin/issues/74 . You need to comment the two lines mentioned by paulinus, and the recompile and reinstall Pangolin, if you happen to find this problem. If you still have problems using this program, please contact: gaoxiang12@mails.tsinghua.edu.cn

根据文件操作即可，这部分我没有去实践，大家可以自行探索。