目录

前言

KNN算法

决策树算法

朴素贝叶斯算法

岭回归算法

线性优化算法

---

前言

本篇文章会介绍一些sklearn库中简单的机器学习算法如何使用，一些注释已经写在代码中，帮助一些小伙伴入门sklearn库的使用。

注意：本篇文章只涉及到如何使用，并不会讲解原理，如果想了解原理的小伙伴请自行搜索其他技术博客或者查看官方文档。

KNN算法

from sklearn.datasets import load_iris  # 导入莺尾花数据集的模块
from sklearn.model_selection import train_test_split # 导入划分数据集的模块
from sklearn.preprocessing import StandardScaler  # 导入标准化的模块
from sklearn.neighbors import KNeighborsClassifier  # 导入KNN算法的模块
from sklearn.model_selection import GridSearchCV  # 导入网格搜索和交叉验证的模块（判断k取几的时候KNN算法的准确率最高）iris = load_iris()  # 引入数据集x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target)  # 进行训练集和测试集的划分transfer = StandardScaler()  # 标准化操作
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)estimator = KNeighborsClassifier()  # KNN算法
param_dict = {'n_neighbors': [1, 3, 5, 7, 9, 11]}  # 以字典的形式传入
estimator = GridSearchCV(estimator, param_grid=param_dict,cv=10)  # 网格搜索
estimator.fit(x_train, y_train)
y_predict = estimator.predict(x_test)
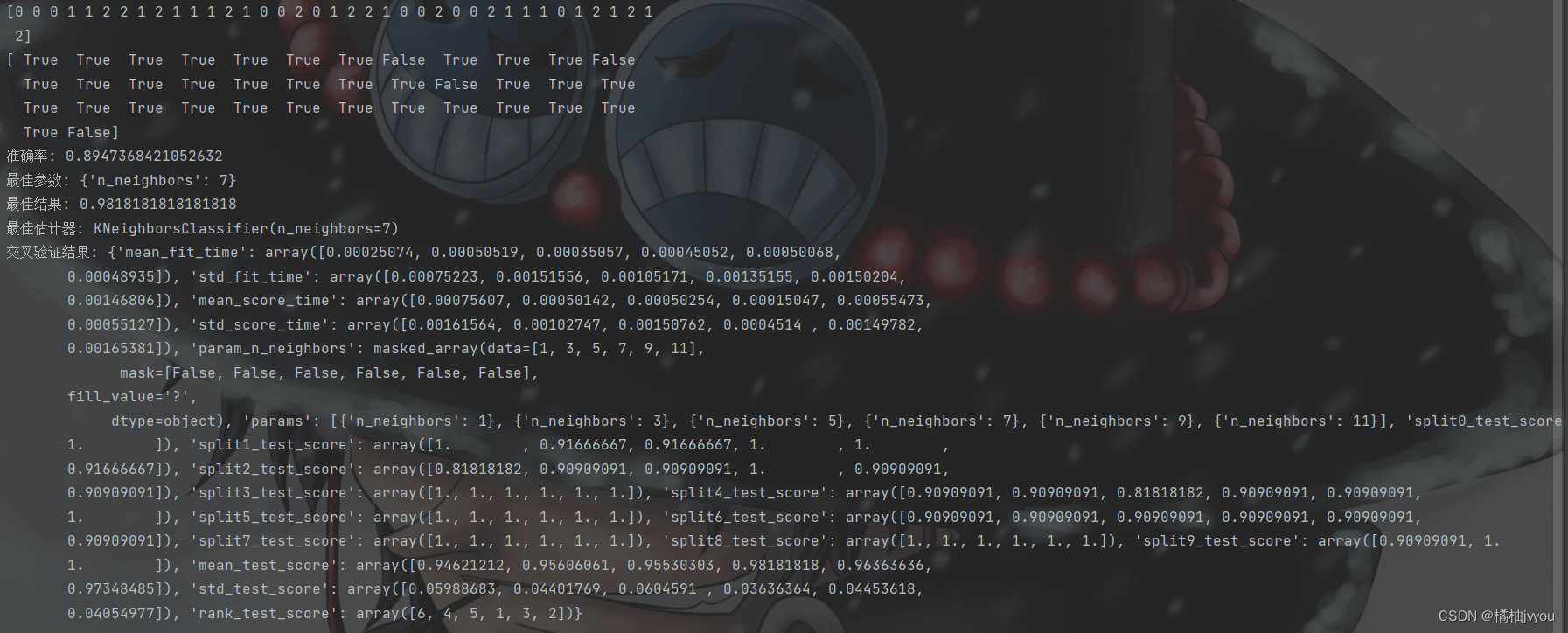
print(y_predict)
print(y_predict == y_test)
r = estimator.score(x_test, y_test)
print('准确率:', r)
print('最佳参数:', estimator.best_params_)
print('最佳结果:', estimator.best_score_)
print('最佳估计器:', estimator.best_estimator_)
print('交叉验证结果:', estimator.cv_results_)

决策树算法

from sklearn.datasets import load_iris  # 导入莺尾花数据集的模块
from sklearn.model_selection import train_test_split  # 导入划分数据集的模块
from sklearn.tree import DecisionTreeClassifier  # 导入决策树算法的模块
from sklearn import tree  # 导入决策树可视化的模块
import matplotlib.pyplot as pltiris = load_iris()  # 引入数据集x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target)  # 进行训练集和测试集的划分estimator = DecisionTreeClassifier(criterion='entropy')  # 按照信息增益决定特征分别位于树的那层
estimator.fit(x_train, y_train)
y_predict = estimator.predict(x_test)
print(y_predict)
print(y_predict == y_test)
r = estimator.score(x_test, y_test)
print('准确率:', r)plt.figure(figsize=(10, 10))
tree.plot_tree(estimator, feature_names=iris.feature_names)  # 决策树可视化
plt.show()

 

 朴素贝叶斯算法

# 计算概率，那种的概率大就把它划分为那种
from sklearn.datasets import load_iris  # 导入莺尾花数据集的模块
from sklearn.model_selection import train_test_split  # 导入划分数据集的模块
from sklearn.naive_bayes import MultinomialNB  # 导入朴素贝叶斯算法的模块iris = load_iris()  # 引入数据集x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target)  # 进行训练集和测试集的划分estimator = MultinomialNB()  # 朴素贝叶斯算法
estimator.fit(x_train, y_train)
y_predict = estimator.predict(x_test)
print(y_predict)
print(y_predict == y_test)
r = estimator.score(x_test, y_test)
print('准确率:', r)

 

岭回归算法

# 用岭回归对波士顿房价进行预测
from sklearn.datasets import load_boston  # 导入波士顿房价的模块
from sklearn.model_selection import train_test_split  # 导入数据集划分的模块
from sklearn.preprocessing import StandardScaler  # 导入标准化的模块
from sklearn.linear_model import Ridge  # 导入岭回归算法的模块
from sklearn.metrics import mean_squared_error  # 导入均方误差的模块boston = load_boston()
print('特征数量：', boston.data.shape)x_train, x_test, y_train, y_test = train_test_split(boston.data, boston.target, random_state=22)  # 进行数据集划分，最后一个参数是设定随机数种子transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)estimator = Ridge()
estimator.fit(x_train, y_train)
y_predict = estimator.predict(x_test)
error = mean_squared_error(y_test, y_predict)
print('岭回归-权重系数(k)为:', estimator.coef_)
print('岭回归-偏置(b)为:', estimator.intercept_)
print('岭回归-均方误差为:', error)

线性优化算法

# 几个特征对应几个权重系数:y=k1x1+k2x2+k3x3+k4x4+.....+knxn+b
# 对波士顿房价进行预测
# 正规方程优化算法和梯度下降优化算法
from sklearn.datasets import load_boston  # 导入波士顿房价的模块
from sklearn.model_selection import train_test_split  # 导入数据集划分的模块
from sklearn.preprocessing import StandardScaler # 导入标准化的模块
from sklearn.linear_model import LinearRegression, SGDRegressor  # 导入正规方程算法和梯度下降算法的模块
from sklearn.metrics import mean_squared_error  # 导入均方误差的模块（判断两个算法那个更优，均方误差越小的算法越优）boston = load_boston()
print('特征数量：', boston.data.shape)x_train, x_test, y_train, y_test = train_test_split(boston.data, boston.target, random_state=22)  # 进行数据集划分，最后一个参数是设定随机数种子transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)estimator = LinearRegression()
estimator.fit(x_train, y_train)
y_predict = estimator.predict(x_test)
error=mean_squared_error(y_test, y_predict)
print('正规方程-权重系数(k)为:', estimator.coef_)
print('正规方程-偏置(b)为:', estimator.intercept_)
print('正规方程-均方误差为:', error)estimator = SGDRegressor()
estimator.fit(x_train, y_train)
y_predict = estimator.predict(x_test)
error = mean_squared_error(y_test, y_predict)
print('梯度下降-权重系数(k)为:', estimator.coef_)
print('梯度下降-偏置(b)为:', estimator.intercept_)
print('梯度下降-均方误差为:', error)