1、选择题
1.1、若有以下程序
main()
{ char a='1',b='2';
printf("%c,",b++);
printf("%d\n",b-a); }
程序运行后的输出结果是 C
A)3,2 B)50,2
C)2,2 D)2,50
解析:b++是先赋值后自加,所以打印出来的是2,自加之后b=3,b-a的值是3-1=2,所以打印出2,所以结果是2,2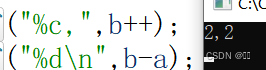
1.2、有以下程序
main()
{
int a,b,d=25;
a=d/10%9;
b=a&&(-1);
printf("%d,%d\n",a,b);
}
程序运行后的输出结果是 B
A)6,1 B)2,1
C)6,0 D)2,0
解析:首先,a=d/10%9=25/10%9=2%9=2,b=a&&(-1),为逻辑运算,只判断真假,a=2为真,-1为真,逻辑与运算之后的结果为真,所以b=1,所以打印的结果是2,1
1.3、若整型变量a、b、c、d中的值依次为:1、4、3、2。则条件表达式a<b?a:c<d?c:d的值 A
A)1 B)2 c)3 D)4
解析:三目运算符(条件表达式?表达式1:表达式2;)的条件表达式成立时执行表达式1,否则执行表达式2,a<b?a:c<d?c:d为一个三目运算符作为另一个三目运算符的表达式2,所以先看a<b?:1<4成立,所以执行表达式1:a,就是1。
1.4、若给定条件表达式(m)?(a++): (a--),则其中表达式m 。 C
A. 和(m= =0)等价 B. 和(m= =1)等价
C. 和(m!=0)等价 D. 和(m!=1)等价
解析:在(m)?(a++): (a--),三目运算里条件表达式(m)?是判断m是否为真,等价于m不为0,即m!=0
1.5、以下选项中,当x为大于1的奇数时,值为0的表达式 D
A. x%2==1 B. x/2 C. x%2!=0 D. x%2==0
解析:奇数对2取余的值一定为1,所以x%2==1为真,即表达式的值为1,x/2一定>=1,不为0,所以x/2也为真,即表达式的值也是1,同理,x%2!=0也成立,为真,即表达式的值也是1,x%2==0为假,即表达式的值为0
1.6 有如下程序段,输出结果为 C
int i = 1;
int j = i++;
if( (i>j++) || (i++ == j) ) i+=j;
printf(“%d\n” , i );
A. 2 B. 3 C. 4 D. 5
解析:j=i++,被赋值为i的当前值1,之后i自增1为2,接下来是一个if语句,其中包含两个条件,用逻辑或||连接。C 语言中的逻辑或运算符具有短路特性,即如果第一个条件为真,则不会检查第二个条件。第一个条件是(i>j++)。由于此时i的值是 2,j的值是 1,所以i>j为真。但是,这里还有一个j++操作,它会在比较之后执行,使j自增 1 变为 2。不过,由于第一个条件已经为真,if语句中的逻辑或操作不会检查第二个条件(i++ == j)。所以i=2,j=2,然后执行i+=j,i=i+j=2+2=4
1.7设 int a=12; 表达式a+=a-=a*=a的值是 C 。
A 12 B 144 C 0 D 132
解析:从右往左执行:a*=a=a*a=12*12=144,即此时a=144,然后a-=144=a-144=144-144=0,此时a=0,然后a+=0=0+0=0,此时a=0
1.8若整型变量a、b、c、d中的值依次为:1、4、3、2。则条件表达式a>b?a:c<d?c:d的值 B
A)1 B)2 c)3 D)4
解析:首先a>b?:1>4不成立,所以执行表达式2(c<d?c:d):c<d?:3<2不成立,执行这个里面的表达式2(d),即为2
1.9 有以下程序
main()
{ int i=1,j=2,k=3;
if(i++==1&&(++j==3||k++==3))
printf("%d %d %d\n",i,j,k);
}
程序运行后的输出结果是 D
A)1 2 3 B)2 3 4
C)2 2 3 D)2 3 3
解析:i++==1&&(++j==3||k++==3)先判断i++==1成立,之后i自加为2,(++j==3||k++==3)先判断++j==3成立,j=3所以后面的k++==3就不用判断了,所以k还是3,即输出2,3,3
2、填空题
2.1设a=12,n=5,则计算了表达式a%=(n%=2)后,a的值为 0 ,计算了表达式a+=a-=a*=a后,a的值为 0
解析:a%=(n%=2):n初始值为 5,n%2 的结果是 1(5 除以 2 的余数是 1),因此n=1。即a%=1,=a%1=0任何数除以 1 的余数都是 0(除了 0 本身)
a+=a-=a*=a:从右往左执行:a*=a=a*a=12*12=144,即此时a=144,然后a-=144=a-144=144-144=0,此时a=0,然后a+=0=0+0=0,此时a=0
2.2 设x=2.5,a=7,y=4.7,则x+a%3*(int)(x+y)%2/4的值为 2.75 。
解析:x+a%3*(int)(x+y)%2/4=x+1*(int)(x+y)%2/4=x+1*11%2/4=x+1/4=2.5+0.25=2.75
2.3 设a=2,b=3,x=3.5,y=2.5,则(float)(a+b)/2+(int)x%(int)y的值为 3.5 。
解析:(float)(a+b)/2+(int)x%(int)y=(2+3)/2+3%2=2+1=3.5
2.4以下程序运行后的输出结果是 10 20 0
main()
{
int a,b,c
a=10;b=20;c=(a%b<1)||(a/b>1);
printf("%d %d %d\n",a,b,c);
}
解析:c=(a%b<1)||(a/b>1):首先a%b=10%20=10>1,所以表达式a%b<1为假,a/b=10/20=0,所以a/b>1也为假,在逻辑运算或的规律是有真则真,全假才假,所以表达式(a%b<1)||(a/b>1)为假,所以c=0,即打印出来的是10 20 0
2.5以下程序运行时若从键盘输入:B33<回车>.输出结果是
#include "stdio.h"
main()
{
char a;
int b;
a=getchar();
scanf("%d",&b);
a = a - 'A' + '0';
b = b * 2;
printf("%c %c\n",a,b);
}
解析:getchar()函数读取第一个字符 'B',并将其赋值给a。scanf("%d",&b);读取接下来的整数 "33",并将其赋值给b。a的值从 'B' 转换为对应的数字。转换的逻辑是a = a - 'A' + '0';。因为 'B' 的 ASCII 值是 66,'A' 的 ASCII 值是 65,所以'B'-'A'的结果是 1。再加上 '0'(其 ASCII 值是 48),最终a的值变为 1 + 48 = 49,即字符 '1'。a的值从 33 乘以 2,得到 66。![]()
2.6设a、b、c均为int型变量且a=7.5, b=2,c=3.6, 则表达式a>b && c>a || a<b && !c>b的值是 0 。
解析:a=7.5, b=2,c=3.6,a>b 是7>2,为真。c>a 是3>7,为假,a<b 是7<2,为假。!c>b是!3>2,首先!3是0,然后0>2是假。a>b && c>a结果是假。a<b && !c>b是 结果也是假,因此,表达式a>b && c>a || a<b && !c>b的值是假。
2.7设a、b、c均为int型变量且a=6, b=4,c=2, 则表达式!(a-b)+c-1 && b+c/2的值是 。
解析:!(a-b)+c-1 && b+c/2=!(6-4)+2-1&&4+2/2=!2+2-1&&4+1=0+2-1&&5=1&&5=1
2.8设a、b均为int型变量且a=2, b=4, 则表达式!(x=a) || (y=b) && 0的值是 0 。
解析:!(x=a)|| (y=b) && 0=!(x=2)||(y=4)&&0=0||1&&0=1&&0=0
2.9设a、b、c均为int型变量且a=1, b=4,c=3, 则表达式!(a<b) || !c && 1的值是 0 。
解析:!(a<b) || !c && 1=!(1<4)||!3&&1=!1||!3&&1=0||0&&1=0&&1=0
2.10 若有条件“2<x<3或x<-10”,其对应的C语言表达式是
解析:2<x<3为x>2&&x<3,或x<-10是||x<-10,即表达式为:x>2&&x<3||x<-10
3、填空题
3.1、 编写程序,从标准输入读取字符,并把它们写到标准的输出中。除了大写字母变换成小写字母外,所有字符的输出形式与它们的输入形式相同。
代码:
#include <iostream>
using namespace std;
int main()
{char str;//定义一个字符串存储输入的数据while(cin >> str)//从终端获取输入的字符串{// 如果字符是大写字母,则转换为小写字母if (str>='A'&&str<='Z'){str=str-'A'+'a';}// 输出字符cout << str;}return 0;
}
结果:
![]()
4、分析题
4.1、 思考一下,有两个整形变量a与b,如何在不使用第3个变量的情况下,实现a与b变量值的交换
方法一: 异或
#include <iostream>
using namespace std;
int main()
{int a=10,b=20;a=a^b;b=a^b;a=a^b;cout << a << " " << b << endl;return 0;
}
结果:
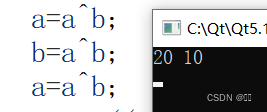
方法二:加减
#include <iostream>
using namespace std;
int main()
{int a=10,b=20;a=a+b;b=a-b;a=a-b;cout << a << " " << b << endl;return 0;
}
结果:
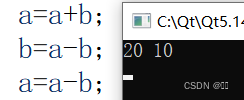



)
![P8756 [蓝桥杯 2021 省 AB2] 国际象棋 状压dp统计情况数的一些小理解](http://pic.xiahunao.cn/P8756 [蓝桥杯 2021 省 AB2] 国际象棋 状压dp统计情况数的一些小理解)










)

【被封印的创世神】)

