第六章 图
6.1 图的基本概念
- 概念
-
图的概念:G由点集V和边集E构成,记为G=(V,E),边集可以为空,但是点集不能为空
·注意:线性表可以是空表,树可以是空树,但图不可以是空,即V一定是非空集
-
无向图与有向图
-
无向图
-
无向边(简称边)
-
无序对,例如(a,b)=(b,a),表示a和b两个点相连
-
-
有向图
-
有向边(简称弧)
-
有序对,例如<v,w>,称为从顶点v指向顶点w的弧,其中v称为弧尾,w称为弧头,<v,w>≠<w,v>,
-
-
-
简单图与多重图(数据结构课程只探讨 简单图)
-
简单图(包含简单有向图、简单无向图)
-
不存在重复边
-
不存在顶点到自身的边
-
-
多重图
-
图G中某两个结点之间的边数多于一条
-
允许顶点通过同一条边和自己关联
-
-
-
顶点的度、入度、出度
-
对于无向图:
-
顶点v的度是指依附于该顶点的边的条数,记为TD(v)
-
无向图每条边贡献两个度,因此n条边的无向图总度数为2n
-
-
对于有向图:
-
入度是以顶点v为终点的有向边的数目,记为ID(v)
-
出度是以顶点v为起点的有向边的数目,记为OD(v)
-
顶点v的度等于其入度和出度之和,即TD(v) = ID(v) + OD(v)
-
有向图每个边贡献一个入度和一个出度,因此有向图总出度等于总入度等于边的个数
-
-
-
顶点与顶点的关系
-
路径:
-
顶点a到顶点b之间的一条路径是指顶点序列,acde…fgb
-
有向图的路径方向必须符合有向边的方向
-
有向图和无向图均有不存在路径的情况:
-
无向图一个孤立点没有任何边——没有到这点的路径
-
有向图一个点没有被任何弧头指到——没有路径
-
-
-
回路:第一个顶点和最后一个顶点相同的路径称为回路或环
-
简单路径:在路径序列中,顶点不重复出现的路径称为简单路径。
-
简单回路:除第一个顶点和最后一个顶点外,其余顶点不重复出现的回路称为简单回路
-
路径长度:路径上边的数目
-
点到点的距离:从顶点u出发到顶点v的最短路径若存在,则此路径的长度称为从u到v的距离,若从u到v根不不存在路径,则记该距离为无穷 (∞)
-
无向图中,若从顶点v到顶点w有路径存在,则称v和w是连通的
-
有向图中,若从顶点v到顶点w和从顶点w到顶点v之间都有路径,则称这两个顶点是强连通的
-
连通图:若无向图G中任意两个顶点都是连通的,则称图G为连通图,否则称为非连通图。
-
对于n个顶点的无向图G,若G是连通图,则最少有 n-1 条边
-
对于n个顶点的无向图G,若G是非连通图,则最多可能有条边
-
-
强连通图:若有向图中任何一对顶点都是强连通的,则称此图为强连通图
-
对于n个顶点的有向图G若G是强连通图,则最少有(n)条边(形成回路)
-
-
-
-
图的局部
-
子图:设有两个图G=(V,E)和G’=(V,E),若V是V的子集,且E’是E的子集,不存在边两端的任何一端没有点的情况,则称G’是G的子图
-
生成子图:包含原图的所有顶点,和部分边的子图
-
连通分量:无向图中的极大连通子图(子图必须连通并且包含尽可能多的顶点和边)
-
强连通分量:有向图中的极大强连通子图(子图必须连通并且包含尽可能多的边)
-
生成树:连通图的生成树是包含图中全部顶点的一个极小连通子图
-
(保持连通且边尽可能少)
-
若图中顶点数为n,则它的生成树含有 n-1条边。
-
对生成树而言,若砍去它的一条边,则会变成非连通图,若加上一条边则会形成一个回路。
-
应用场景:用最少的道路(边)树,连接所有地区(点)
-
-
生成森林:在非连通图中,连通分量的生成树构成了非连通图的生成森林
-
边的权:在一个图中,每条边都可以标上具有某种含义的数值,该数值称为该边的权值。
-
带权图/网:边上带有权值的图称为带权图,也称网。
-
带权路径长度:当图是带权图时,路径上所有边的权值之和,称为该路径的带权路径长度
-
-
几种特殊形态的图
-
无向完全图:无向图中任意两个顶点之间都存在边
- 若无向图的顶点数|V|=n,则
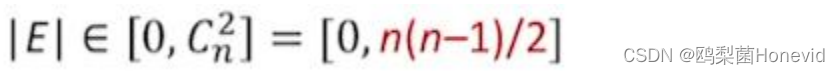
- 若无向图的顶点数|V|=n,则
-
有向完全图:有向图中任意两个顶点之间都存在方向相反的两条弧
- 若有向图的顶点数|V|=n,则
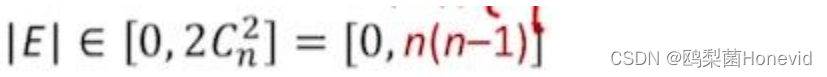
- 若有向图的顶点数|V|=n,则
-
稀疏图与稠密图:边数很少的图称为稀疏图反之称为稠密图
-
树:不存在回路,且连通的无向图
-
n个顶点的树,必有n-1条边
-
n个顶点的图,若边数大于n-1,则一定有回路
-
树是连通图(无向图)
-
-
有向树:1个顶点的入度为0,其余顶点的入度均1有向图,称为有向树
- 有向树是有向图,但不是强连通图
-

- 理解
-
连通图:连起来就行,最少的马路连通最多的村子
-
完全图:每个点,都除他以外的所有点,完全连接
- 技巧
-
当有n个点,若边数等于n-1,则无环连通,但若边数超过n-1,则有环未必连通
-
有n个顶点的无向图,边数v的几个临界值:
-
如果v<n-1,一定不是连通图
-
如果n-1≤v< C n − 1 2 + 1 C_{n - 1}^{2} + 1 Cn−12+1,则可能是连通图,也可能不是
-
如果v> C n − 1 2 + 1 C_{n - 1}^{2} + 1 Cn−12+1,则一定是连通图(确保n个顶点连通的思路:n-1个顶点形成完全图,再加上一个边,那么一定连通)
-

)

【被封印的创世神】)



)
![[算法学习]](http://pic.xiahunao.cn/[算法学习])
-前端框架)

项目概述)
)




原理)

