操作环境:
MATLAB 2022a
1、算法描述
D2D蜂窝通信介绍
D2D蜂窝通信允许在同一蜂窝网络覆盖区域内的终端设备直接相互通信,而无需数据经过基站或网络核心部分转发。这种通信模式具有几个显著优点:首先,它可以显著降低通信延迟,因为数据传输路径更短;其次,由于减少了基站的中转,可以提高数据传输的能效,从而延长终端设备的电池寿命;再次,D2D通信可以提高系统容量和频谱效率,因为同一地理区域内的频谱可以被重复利用;最后,它还可以增强蜂窝网络的覆盖,特别是在网络边缘或传统基站无法覆盖的区域。
在D2D通信的实现中,存在几个关键技术挑战,包括用户发现、功率控制、资源分配和干扰管理。用户发现是指如何有效识别和选择在物理上靠近的设备进行D2D通信。功率控制涉及确定适当的发射功率水平,以确保通信质量同时最小化对其他用户的干扰。资源分配是指如何在D2D用户和蜂窝用户之间高效分配有限的频谱资源。干扰管理则是确保D2D通信不会对蜂窝网络中的其他用户造成不可接受的干扰。
启发式算法在D2D中的应用
在D2D蜂窝通信中,启发式算法主要用于解决资源分配和功率控制问题。这些算法通常基于某些简化的规则或经验,以快速找到问题的可行解。例如,一种简单的启发式方法是基于信道状态信息(CSI)的用户配对策略,其中选择信道条件最佳的用户对进行D2D通信,以此来最大化系统吞吐量或最小化总功率消耗。
然而,启发式算法也存在一定的局限性。由于它们通常基于局部信息做出决策,因此可能无法达到全局最优。此外,这些算法的性能在很大程度上依赖于设计时考虑的特定场景和假设,可能在网络环境发生变化时性能下降。
最优化算法的角色
最优化算法在D2D蜂窝通信中的应用包括但不限于功率控制、资源分配和信道选择。这些算法试图找到数学意义上的最优解,以达到如最大化网络吞吐量、最小化能耗或优化服务质量(QoS)等目标。
例如,可以通过建立一个优化模型来描述网络吞吐量与D2D对的功率分配、频谱分配之间的关系。然后,应用诸如拉格朗日乘数法、对偶分解或内点法等数学优化技术来求解该模型,寻找最优解。这些方法能够提供精确的解决方案,但它们的计算复杂度较高,特别是在用户数量和网络规模较大时,求解过程可能变得非常耗时。
随机算法的应用
随机算法通过引入随机性来探索解空间,能够在复杂或不确定的环境中找到问题的近似最优解。在D2D蜂窝通信中,这类算法特别适用于动态变化的网络环境,如动态的用户分布、变化的信道条件等。
遗传算法是一种模拟自然进化过程的随机算法,它通过选择、交叉和变异等操作在解的种群中引导搜索过程。在D2D通信的资源分配问题中,遗传算法可以用于在多个目标之间寻找权衡,如在系统吞吐量和用户公平性之间。模拟退火算法模仿金属退火过程,通过逐渐降低“温度”来减少解的随机搜索范围,有效地避免陷入局部最优解。粒子群优化算法则通过模拟鸟群的社会行为来更新解,适用于连续空间的优化问题。
这些随机算法能够在较宽的范围内探索解空间,找到满意的解决方案,但它们的性能依赖于算法参数的选择,且通常无法保证找到全局最优解。
总体而言,D2D蜂窝通信中的启发式算法、最优化算法和随机算法各有优缺点。启发式算法实现简单、计算效率高,适用于实时或近实时的场景,但可能无法保证找到全局最优解。最优化算法能够提供理论上的最优解,但在面对大规模或高度复杂的问题时,计算复杂度可能非常高。随机算法提供了一种灵活的解决方案,能够在可接受的时间内找到满意的解,特别适合于解决传统算法难以处理的优化问题。在实际应用中,根据具体问题的特点和需求,选择合适的算法类型是关键。
结论
D2D蜂窝通信技术为提高蜂窝网络的性能和效率提供了新的途径。在实现这一目标的过程中,启发式算法、最优化算法和随机算法各有其独特的优势和适用场景。选择合适的算法不仅取决于问题本身的特性,也依赖于实际应用中的具体要求,如解的质量、算法的复杂度和执行时间等。通过合理选择和设计算法,可以有效地解决D2D蜂窝通信中的关键问题,推动5G及未来网络技术的发展。
2、仿真结果演示
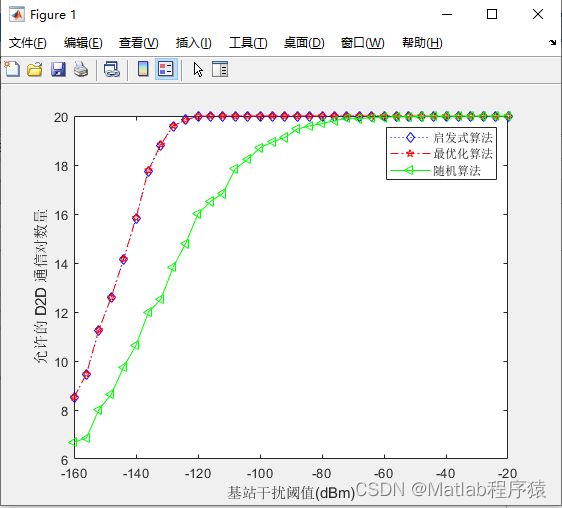
3、关键代码展示
4、MATLAB 源码获取
V
点击下方名片




![猫头虎分享已解决Bug || RuntimeError: size mismatch, m1: [32 x 100], m2: [500 x 10]](http://pic.xiahunao.cn/猫头虎分享已解决Bug || RuntimeError: size mismatch, m1: [32 x 100], m2: [500 x 10])
)




:Linux的vi/vim编辑器)


)
)




