简介:在计算机科学中是指一种通过重复将问题分解为同类的子问题而解决问题的方法。通过函数的自调用化繁为简。
递归可以说是编程中最神奇的一种算法。因为我们有时候可能不能完全明晰代码的运行过程,但是我们却知道代码可以跑出正确的结果。而当我们使用其他算法,我们必须将代码运行的每一个细节都弄清楚才能确保代码的正确性。这就是递归的神奇之处。
下面由浅入深对递归进行解析:
1.阶乘计算
相信这是每个人初学递归时都会遇到的问题。当然这也是最容易理解的一种递归,思路很简单:
如果要计算n的阶乘,我们可以先算出n-1的阶乘再乘上n,如果要计算n-1的阶乘,我们可以先算出n-2的阶乘再乘上n-1,依此类推,递归逐渐深入,我们只需要给出1的阶乘和0的阶乘,然后递归就会不断返回,最后算出n的阶乘。
这一点还是比较容易理解,此处不作赘述。
int f(int n)
{if (n == 0 || n == 1)return 1;elsereturn n * f(n - 1);
}2.爬楼梯
爬楼梯OJ
题目概述:
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
这也是一个典型可以用递归解决的问题
思路:如果我们要到达n阶,我们可以从n-1阶往上跳一个台阶,或者从n-2阶往上跳2个台阶,我们可以想想是不是只有这两种情况?所以到达n阶的方法数量是不是就是到达n-1阶的方法数量和到达n-2阶的方法数量之和?答案是显然的。那么这个问题是不是就和第一个例题类似了,只是这里的递归分支了,但是本质上是相同的,我们只需要给出到达1阶和到达2阶的方法数量,递归就能返回到n阶的方法数量。
int climbStairs(int n){if(n==1)return 1;else if(n==2)return 2;elsereturn climbStairs(n-1)+climbStairs(n-2);
}需要注意的是:这里给出的代码并不能通过,因为分支递归在递归层数过深的时候很容易超时,举个例子,我们要计算到达10阶的方法数,我们要算9阶和8阶.......
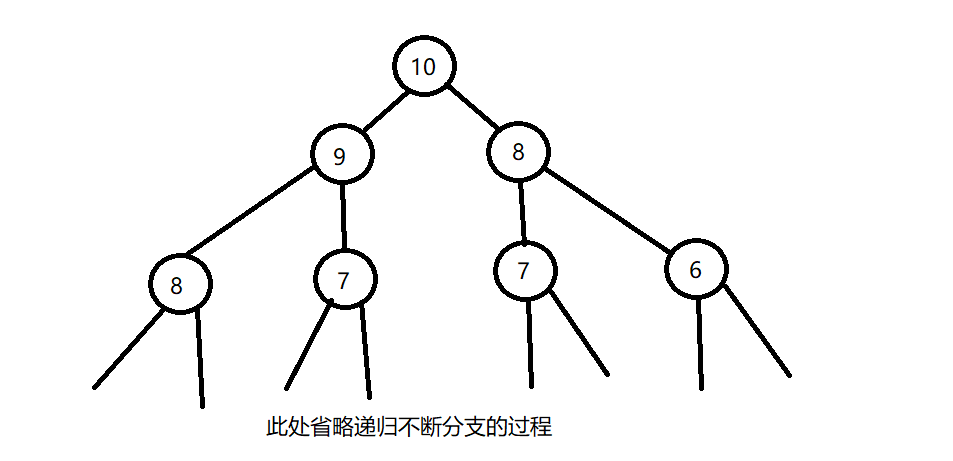
这里递归的时间复杂度是O(2^n),n过大时超时是必然的。如果要避免超时可以使用迭代(循环)代替递归。使用递归的优势是代码逻辑更加明了,而迭代的优势是速度更快,如果递归分支了那么迭代的优势会更加明显。
这里给出迭代的方法仅供参考,不作讨论
int climbStairs(int n){if(n==1)return 1;if(n==2)return 2;int a=1;int b=2;int c;while(n>=3){c=a+b;a=b;b=c;n--;}return c;
}3.找最大值
要求很简单,写一个函数
int find(int*nums,int numsSize)要求返回nums数组的最大值。最简单的方法是定义一个max变量遍历nums并更新max最后返回即可。如果使用递归该怎么做呢?
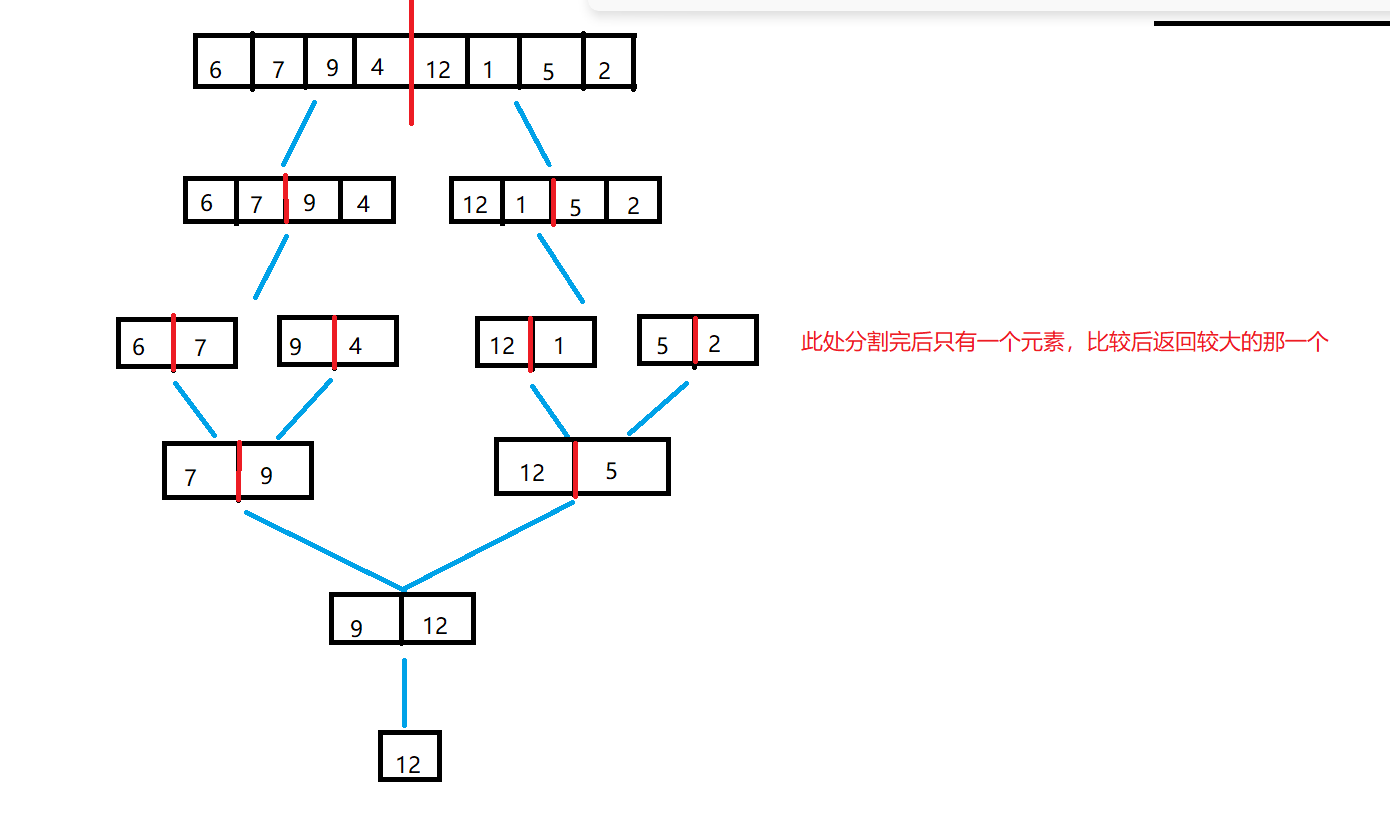
思路:我们将nums平分为左右两个部分,记左半部分最大值为max1,右半部分最大值为max2,那么显然整个nums的最大值是max1和max2中较大的一个。那么同样的,max1和max2是如何得到的呢?我们将左右部分分别再次平分........不断进行下去,知道最后平分完之后一个元素单独组成一个部分,那么这个部分的最大值就是这个单独的元素
int max(int* nums, int numsSize)
{int right = numsSize - 1;if (right == 0)return nums[0];else{int mid = right / 2;return max(nums, mid + 1) > max(nums + mid + 1, right -mid)? max(nums, mid + 1): max(nums + mid + 1, right - mid);}
}以下是一个示意图:
教学视频:
在这里强烈推荐一个视频,视频链接,看完这个视频会对递归以及接下来的问题有更深刻的认识
4.归并排序
从这个部分开始递归就上了一个档次,第三个问题其实是这个问题的铺垫
归并排序的原理:与第三个问题一样,将数组细分直到每个部分只有一个元素,此时每个部分可以看作升序,使用merge函数将两部分合并成一个升序的部分(merge函数是将[4,8,9,10,1,2,3]这样两个部分为升序的数组排成完全升序的数组,力扣上有类似的实现merge函数的OJ 合并两个有序数组,但是这里是仅处理一个数组,只需要进行一些细节处理就能转换成相同问题)
归并排序的实现
void sort(int* arr1, int left, int right)
{if (right == left)return;int mid = left + (right - left) / 2;//将左半部分排序sort(arr1, left, mid);//将右半部分排序sort(arr1, mid + 1, right);//将两个升序部分排成完全升序merge(arr1, left, mid, right);
}merge的实现
void merge(int* arr, int start, int mid, int end)
{int* copy = (int*)malloc(sizeof(int) * (end -start+ 1));memcpy(copy, arr+start,(end-start+1)*sizeof(int));int count = start;int count1 = 0;int count2 = mid-start+1;while (count1 <= mid-start && count2 <= end-start){if (copy[count1] <= copy[count2]){arr[count++] = copy[count1++];}else{arr[count++] = copy[count2++];}}if(count1==mid-start+1){while (count2 <= end-start){arr[count++] = copy[count2++];}}else{while (count1 <= mid-start){arr[count++] = copy[count1++];}}free(copy);
}在上边给出的教学视频里包含详细的动画展示,这里就不画图进行模拟了。
5.汉诺塔问题

有A、B、C三根柱子,初始状态A柱子上有若干个盘子,目标是将A上的所有盘子移动到C柱子上,并且小盘子在上,大盘子在下,与初始状态相同。移动过程中大盘子不能放在小盘子上。
我们设计一个函数
void hano(int n,char a,char b,char c)很多人对函数的四个参数不理解,或者理解不深刻,包括一些博文对几个参数都没有很好的解释。在这里先进行一个简单的分析,在后面的代码中会深入剖析。
参数分析:
很明显n表示A柱子上有n个盘子,奇怪的是为什么要三个char类型变量???其实很简单,这里的三个char类型形参接收的分别常量'A' 'B' 'C'中的一个。这个函数的含义是:将a变量的柱子上的n-1个盘子移动到b变量的盘子上,再将a变量柱子上第n个(最大的)盘子移动到c变量柱子上,最后将b变量柱子上的n-1个盘子移动到c变量柱子上。举个例子:
hano(15,'B','A','C');表示将B柱子上的14个盘子移动到A,再把B上最后一个盘子移动到C上,再把A上n-1个盘子移动到C上
但是n-1个盘子是不能直接移动的,所以具体是怎么移动的呢?
当n=2时,我们会使用这个函数
hano(2,'A','B','C');这样n-1=1,我们每次只会移动一个盘子,就可以直接移动了。
当n=3时,我们需要把2个盘子从A移动到B上,于是我们使用
hano(n-1,'A','C','B');那么怎么把2个盘子移动到B上?我们首先要把1个盘子移动到C上
那么对于n个盘子,我们的思路也一样
//move中的n表示的是 第n个盘子
void move(int n, char soure, char destination)
{printf("move %d from %c to %c\n", n, soure, destination);
}
void hano(int n,char a,char b,char c)
{if (n == 1){move(1, a, c);}else{//将n-1个盘子从a移动到b上//问题:既然是从a到b,那么和第二个参数有什么关系呢?为什么需要第二个参数?hano(n - 1, a, c, b);move(n, a, c);//只有一个盘子了,直接打印出移动轨迹hano(n - 1, b, a, c);}
}现在对代码中提出的问题进行解答:我们再hano函数中再次调用hano,三个参数的值是会来回hano知道这一步的三hano才能推测下一步的三个参数,少一个参数hano函数就不能正常递归了
到了这里文章就结束了,最后再次推荐大家看一看文章给出的视频,看完会对递归有更深刻的认识。









?)






)


)