1. 直接计算法
给定模型![]() 和观测序列
和观测序列![]() ,计算观测序列O出现的概率
,计算观测序列O出现的概率![]() 。最直接
。最直接
的方法是按概率公式直接计算.通过列举所有可能的长度为T的状态序列![]() ,求各个状
,求各个状
态序列 I 与观测序列![]() 的联合概率
的联合概率![]() ,然后对所有可能的状态序列求和,得
,然后对所有可能的状态序列求和,得
到![]() 。
。
状态序列![]() 的概率是
的概率是![]()
对固定的状态序列![]() ,观测序列
,观测序列![]() 的概率是
的概率是![]() 。
。
![]() ,O和I同时出现的联合概率为
,O和I同时出现的联合概率为![]()
![]() 。然后,对所有可能的状态序列I求和,得到观测序列O的概率
。然后,对所有可能的状态序列I求和,得到观测序列O的概率
![]() ,即
,即![]()
![]() 但是,利用公式计算
但是,利用公式计算
量很大,是![]() 阶的,这种算法不可行。
阶的,这种算法不可行。
2. 前向算法
首先定义前向概率。给定隐马尔可夫模型λ,定义到时刻 t 部分观测序列为![]() ,且
,且
状态为q1的概率为前向概率,记作![]() 。可以递推地求得前向概率α(i)
。可以递推地求得前向概率α(i)
及观测序列概率![]() 。
。
算法:(观测序列概率的前向算法)输入:隐马尔可夫模型λ,观测序列O;输出:观测序列概率P
(O|λ)。
初值:![]()
递推:对![]() ,
,![]()
终止:![]()
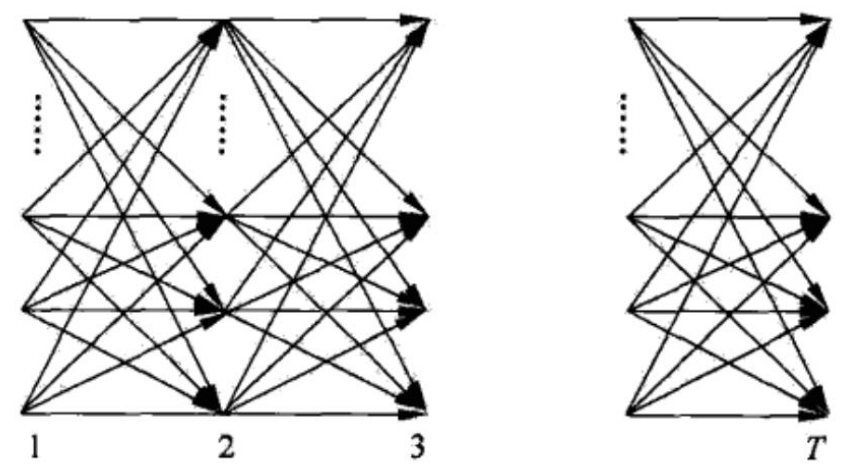

如上图所示,前向算法实际是基于“状态序列的路径结构”递推计算P(O|λ)的算法。前向算法高
效的关键是其局部计算前向概率,然后利用路径结构将前向概率“递推”到全局,得到P(O|λ).
具体地,在时刻t=1,计算α1(i)的N个值(i=1,2,···,N);在各个时刻t=1,2,···,T-1,
计算αt+1(i)的N个值(i=1,2,···.,N),而且每个αt+1(i)的计算利用前一时刻N个αt(j),减少计
算量的原因在于每一次计算直接引用前一个时刻的计算结果,避免重复计算。这样,利用前向概率
计算P(O|λ)的计算量是![]() 阶的,而不是直接计算的
阶的,而不是直接计算的![]() 阶。
阶。
前向算法的复杂度:
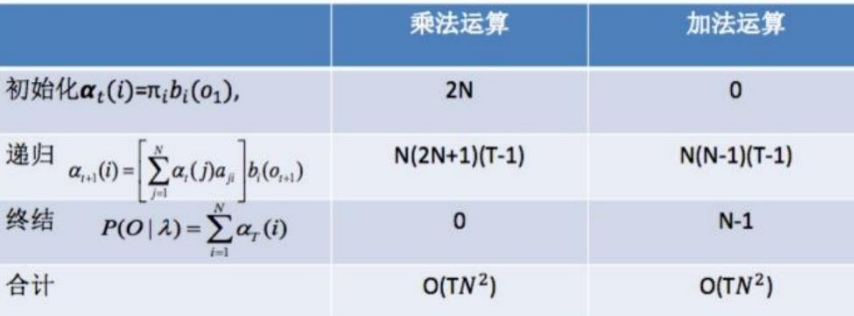
所以利用前向算法计算![]() 的计算量是
的计算量是![]() 阶的,当N=3,T=100时,
阶的,当N=3,T=100时,
原始算法:![]() 大约需要10^(50)次运算;前向算法:
大约需要10^(50)次运算;前向算法:![]() 计算次数小于2000次
计算次数小于2000次
前向算法Python实现分析:
import numpy as np def forward_algorithm(obs, states, start_p, trans_p, emit_p): """ obs: 观察序列 states: 隐藏状态集合 start_p: 初始状态概率 trans_p: 状态转移概率 emit_p: 发射概率 """ T = len(obs) N = len(states) # 初始化alpha alpha = np.zeros((T, N)) alpha[0, :] = start_p * emit_p[:, obs[0]] # 递推计算alpha for t in range(1, T): for n in range(N): alpha[t, n] = sum(alpha[t-1, :] * trans_p[:, n]) * emit_p[n, obs[t]] # 计算观察序列的概率 P = sum(alpha[-1, :]) return P, alpha # 示例
obs = [0, 1, 0] # 观察序列
states = [0, 1] # 隐藏状态集合
start_p = [0.6, 0.4] # 初始状态概率
trans_p = [[0.7, 0.3], [0.4, 0.6]] # 状态转移概率
emit_p = [[0.1, 0.9], [0.9, 0.1]] # 发射概率 P, alpha = forward_algorithm(obs, states, start_p, trans_p, emit_p)
print(f"观察序列的概率: {P}")3. 后向算法
后向概率:给定隐马尔可夫模型λ,定义在时刻t状态为q1的条件下,从t+1到T的部分观测序列为
![]() 的概率为后向概率,记作
的概率为后向概率,记作![]()
可以用递推的方法求得后向概率βt(i)及观测序列概率P(O|λ)。
观测序列概率的后向算法:
输入:隐马尔可夫模型λ,观测序列O;输出:观测序列概率P(O|λ)。
![]() ,对
,对![]()
![]()
![]()
后向算法Python实现分析:
import numpy as np def backward_algorithm(obs, states, start_p, trans_p, emit_p): """ obs: 观察序列 states: 隐藏状态集合 start_p: 初始状态概率 (虽然后向算法本身不使用这个参数,但为了完整性仍然包括在参数列表中) trans_p: 状态转移概率 emit_p: 发射概率 """ T = len(obs) # 观察序列的长度 N = len(states) # 隐藏状态的数量 # 初始化beta beta = np.ones((T, N)) # 从观察序列的倒数第二个元素开始递推计算beta for t in range(T - 2, -1, -1): for n in range(N): beta[t, n] = np.dot(beta[t + 1, :] * emit_p[:, obs[t + 1]], trans_p[n, :]) # 计算观察序列的概率 # 注意:这里我们实际上计算的是所有可能路径的概率之和, # 但由于我们只需要这个总和,因此不需要显式地计算每个路径的概率。 # 初始状态概率start_p在后向算法中并不直接用于计算观察序列的概率, # 但我们可以利用最后一步的beta和初始的发射概率来计算整个观察序列的概率。 # 这是一种不太常见的做法,因为我们通常使用前向-后向算法来计算概率, # 该算法结合了前向和后向概率以避免数值下溢问题。 # 然而,为了这个示例的完整性,我们将展示如何使用beta来计算概率。 # 请注意,这种方法可能不是数值上最稳定的。 # 正确的做法是使用前向-后向算法中的一个步骤来计算概率,如下: # P = sum(forward_probs[-1] * backward_probs[0]) (其中forward_probs和backward_probs是归一化的) # 但在这个例子中,我们只实现后向算法,所以我们将使用一种简化的方法(可能不是最优的)。 # 计算最后一步的"后向概率"(未归一化) last_step_backward = np.dot(beta[0, :] * emit_p[:, obs[0]], start_p) # 由于我们没有计算前向概率,我们不能简单地通过前向和后向概率的乘积来归一化。 # 因此,我们将依赖这样一个事实:对于正确的模型参数,后向算法计算的beta应该使得下面的求和接近1(但不是严格的1,因为数值误差)。 # 在实际应用中,应该使用前向-后向算法来确保正确的归一化。 # 近似计算观察序列的概率(这不是标准做法,仅用于演示目的) P = np.sum(last_step_backward) return P, beta # 示例参数(同前向算法示例)
obs = [0, 1, 0] # 观察序列
states = [0, 1] # 隐藏状态集合(这里用整数表示状态)
start_p = [0.6, 0.4] # 初始状态概率(虽然后向算法不使用它来计算概率)
trans_p = [[0.7, 0.3], [0.4, 0.6]] # 状态转移概率
emit_p = [[0.1, 0.9], [0.9, 0.1]] # 发射概率 # 调用后向算法函数并打印结果
P, beta = backward_algorithm(obs, states, start_p, trans_p, emit_p)
print(f"观察序列的概率(近似): {P}")4. 计算
利用前向概率和后向概率,可以得到关于单个状态和两个状态概率的计算公式。
给定模型λ和观测O,在时刻t处于状态q1的概率。记![]()
可以通过前向后向概率计算。事实上,![]()
由前向概率![]() 和后向概率
和后向概率![]() 定义可知:
定义可知:![]()
于是得到: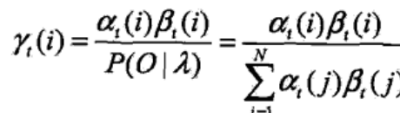
给定模型λ和观测O,在时刻t处于状态qt且在时刻t+1处于状态qj的概率。记
![]()
可以通过前向后向概率计算: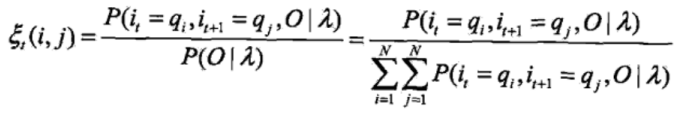
而![]() 所以:
所以: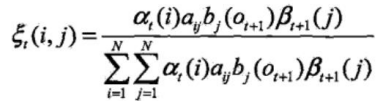
将![]() 和
和![]() 对各个时刻t求和,可以得到一些有用的期望值:
对各个时刻t求和,可以得到一些有用的期望值:
在观测O下状态i出现的期望值![]() ,在观测O下由状态i转移的期望值
,在观测O下由状态i转移的期望值![]()
在观测O下由状态i转移到状态j的期望值![]()
![洛谷 P2678 [NOIP2015 提高组] 跳石头 (Java)](http://pic.xiahunao.cn/洛谷 P2678 [NOIP2015 提高组] 跳石头 (Java))






》笔记8.1)






 证书apiserver_client_certificate_expiration_seconds)




