先看一个背包问题的简单版:
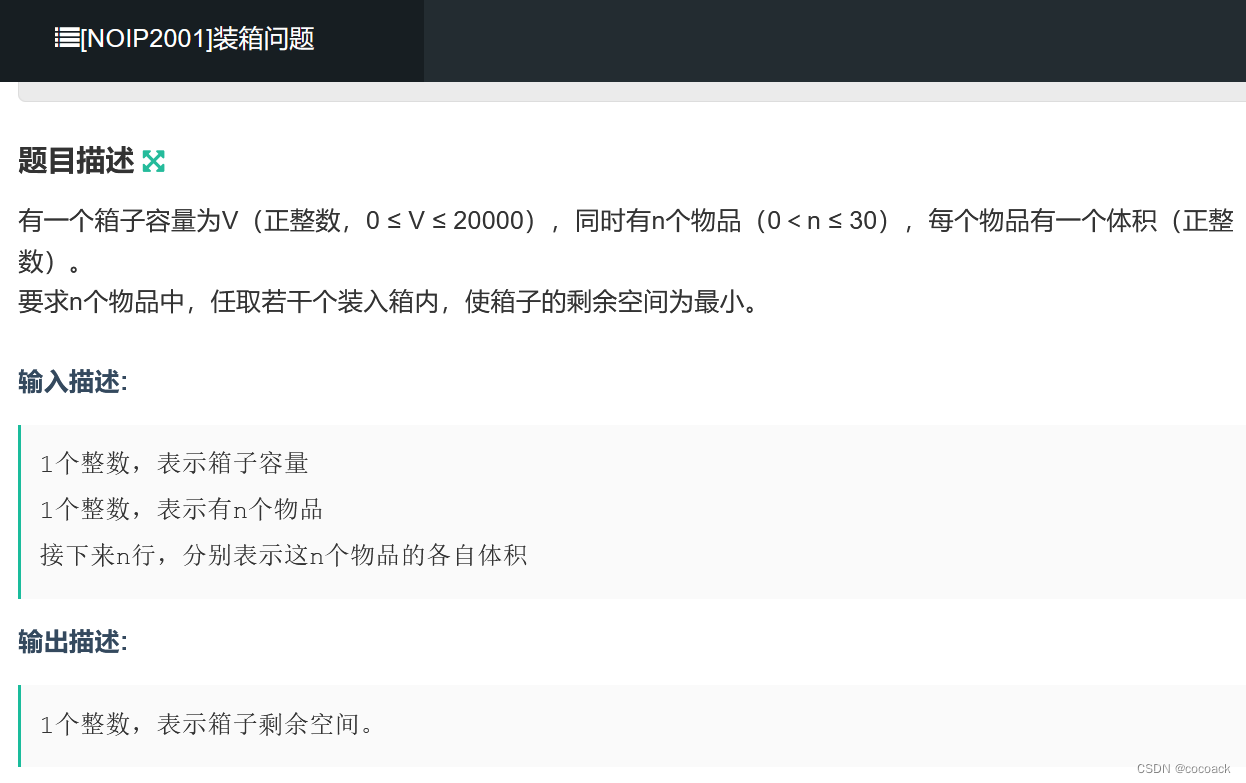
如果我们暴力枚举可能会超时。
但我们想一想,我们其实不关心怎么放,我们关心的是放后剩下的体积。
用可行性描述即可。
于是我们令f[i][j]表示前i个物品能否放满体积为j的背包。
f[i][j]=f[i-1][j]||f[i-1][j-v[i]]; f[0][0]=1;
然后,我们去找jmax并真的值即可。
这是用图表示:
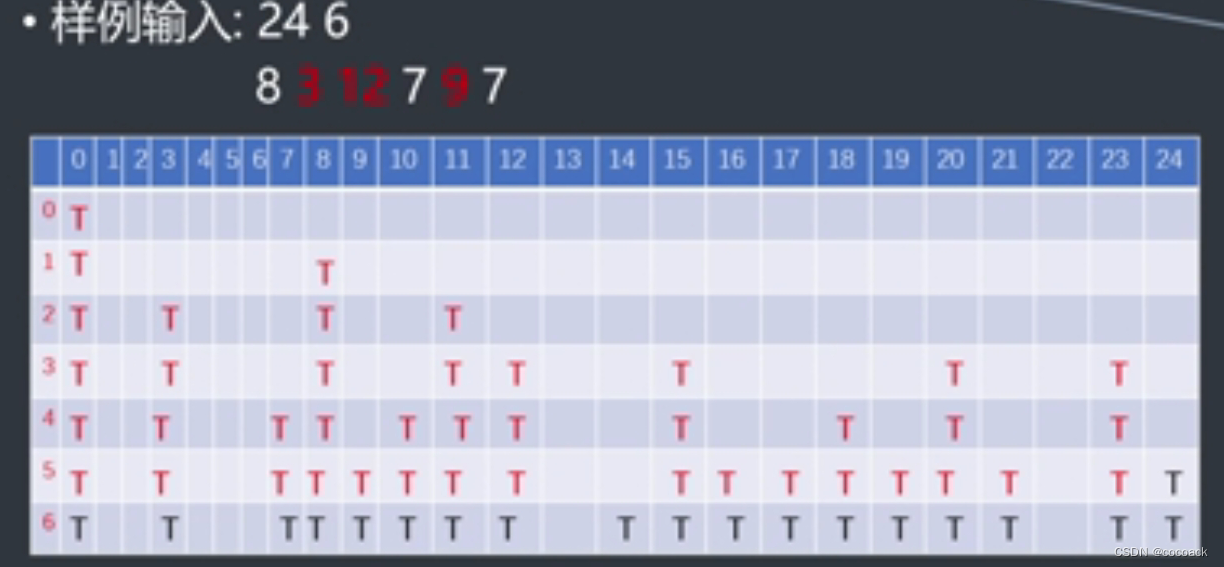
下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
int v,n,a[40][20005],v1[36];
int main(){cin>>v>>n;for(int i=1;i<=n;i++) scanf("%d",&v1[i]);a[0][0]=1;for(int i=1;i<=n;i++){for(int j=0;j<=v;j++){if(j>=v1[i]) a[i][j]=a[i-1][j]||a[i-1][j-v1[i]];else a[i][j]=a[i-1][j];}}for(int i=v;i>=0;i--){if(a[n][i]==1){cout<<v-i;break;}}
}我们用0/1滚动优化一下空间:
#include<bits/stdc++.h>
using namespace std;
int v,n,a[2][20005],v1[36];
int main(){cin>>v>>n;for(int i=1;i<=n;i++) scanf("%d",&v1[i]);a[0][0]=1;for(int i=1;i<=n;i++){for(int j=0;j<=v;j++){if(j>=v1[i]) a[i%2][j]=a[(i-1)%2][j]||a[(i-1)%2][j-v1[i]];else a[i%2][j]=a[(i-1)%2][j];}}for(int i=v;i>=0;i--){if(a[n%2][i]==1){cout<<v-i;break;}}
}进一步,我们想想因为当前行是上一行v1[i]前体积的继承,换句话说,我们可以从v[i]开始枚举,前面的让他继承上一行即可,于是我们可以把数组优化成一维。
但是,这会出现一个问题,我们拿3举例:
当我们在看6时,发现6-3=3为1,于是6也为1,同理,3的倍数的体积全变1,而事实上,我们应该只有3与0为1.
问题在于我们不知道这个真是来自上一行还是这一行刚刚跟新的。
于是,我们可以倒着循环,因为我们发现要跟新依据的都是当前位置前面的,这样,我们这行跟新的只会在后面,这就是就地滚动。
下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
int v,n,a[20005],v1[36];
int main(){cin>>v>>n;for(int i=1;i<=n;i++) scanf("%d",&v1[i]);a[0]=1;for(int i=1;i<=n;i++){for(int j=v;j>=v1[i];j--){a[j]=a[j]||a[j-v1[i]];}}for(int i=v;i>=0;i--){if(a[i]==1){cout<<v-i;break;}}
} 平移,旋转,缩放)

在vue路由中:Vue.use(VueRouter)和Vue.use(Router);有什么区别?)
)


-- 算法导论14.3 5题)









)

-锁的种类与应用场景)
