"Hardships often prepare ordinary people for an extraordinary destiny."
- C.S. Lewis

1. 题目描述
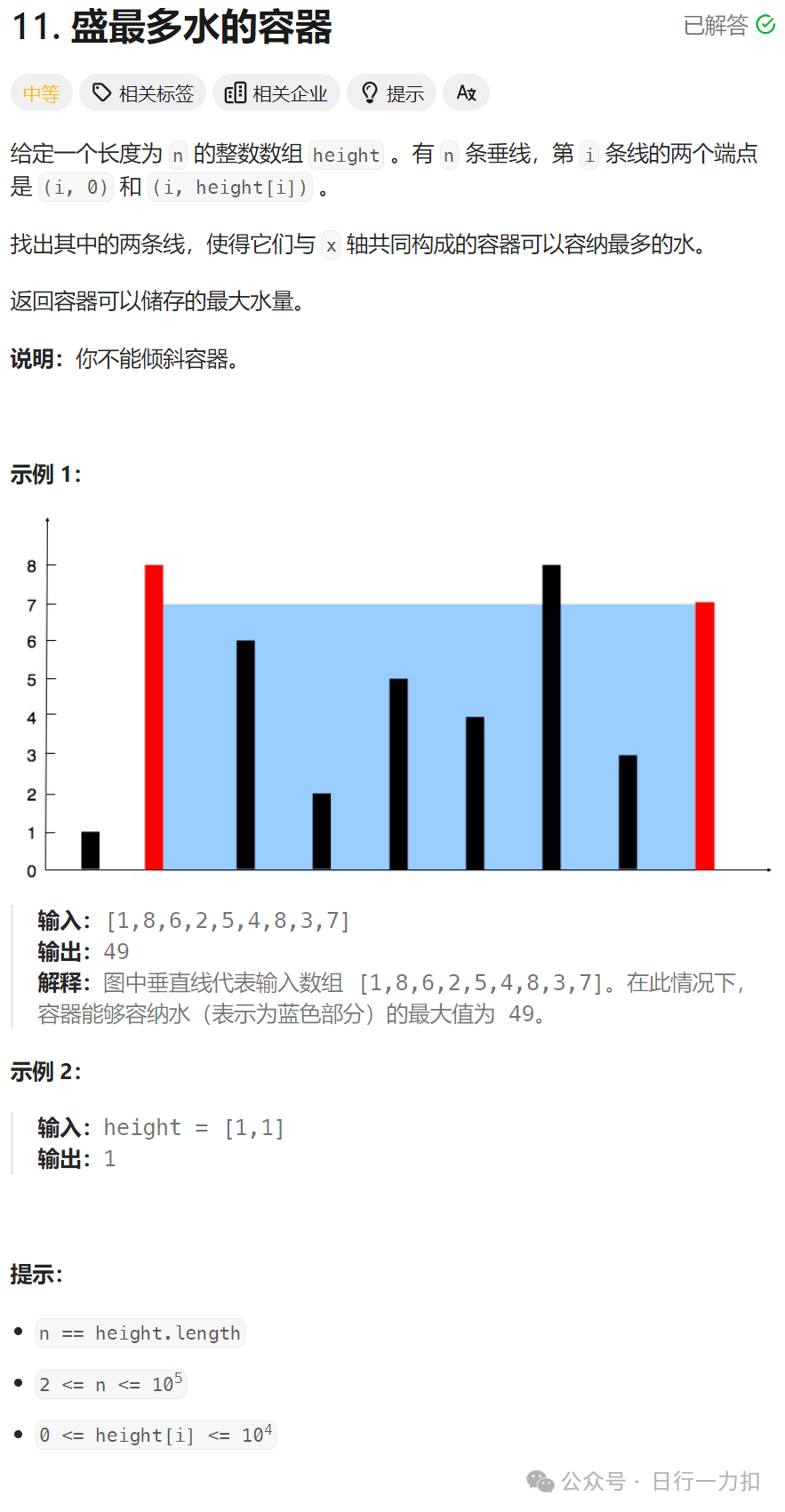
2. 题目分析与解析
2.1 思路一——暴力求解
遇到问题最怕的就是没有思路,就好像人迷茫的时候最怕的就是一直迷茫,不知道怎么干那就先试试最笨的办法,先动起来,大不了就是多花点时间,等后面可以慢慢优化嘛。
暴力求解思路:遍历数组的每一个位置,以它为起始位置,与自身以外的所有元素进行匹配,保留能存的水中最大的值。计算出所有位置的的最大值后,取出所有位置的值中最大的值,可以看下图:
第一次从第一个位置从前向后寻找它(红色)与其它(绿色)的积水量记为黄色:
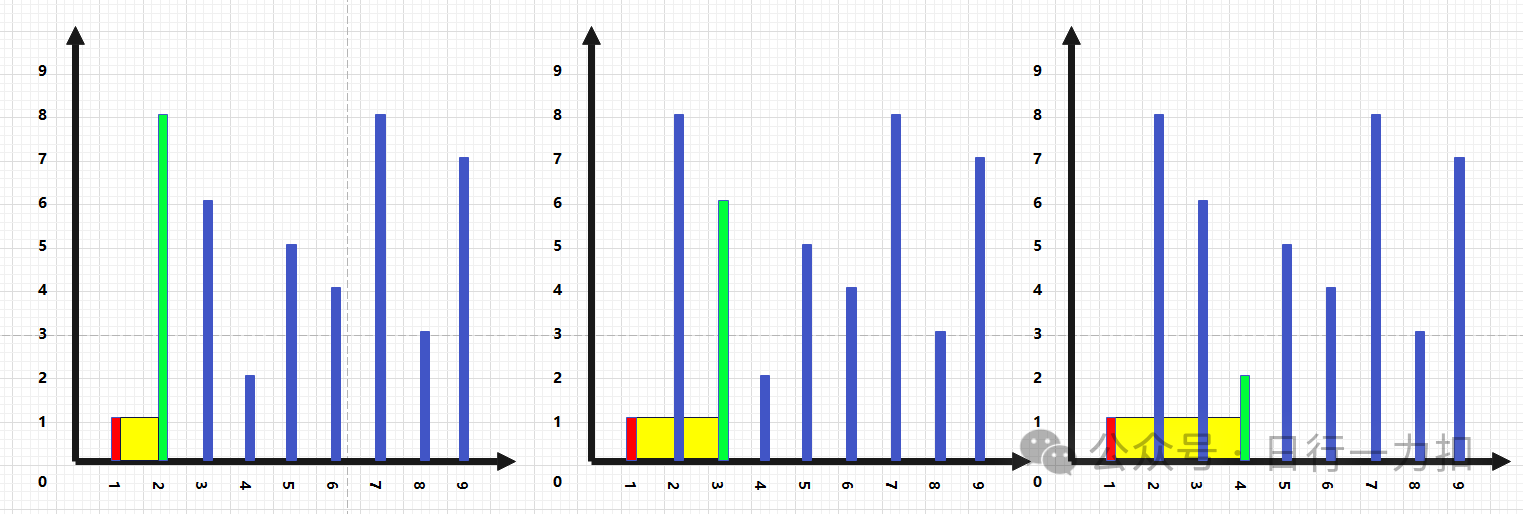
第二次从第二个位置从前向后寻找:
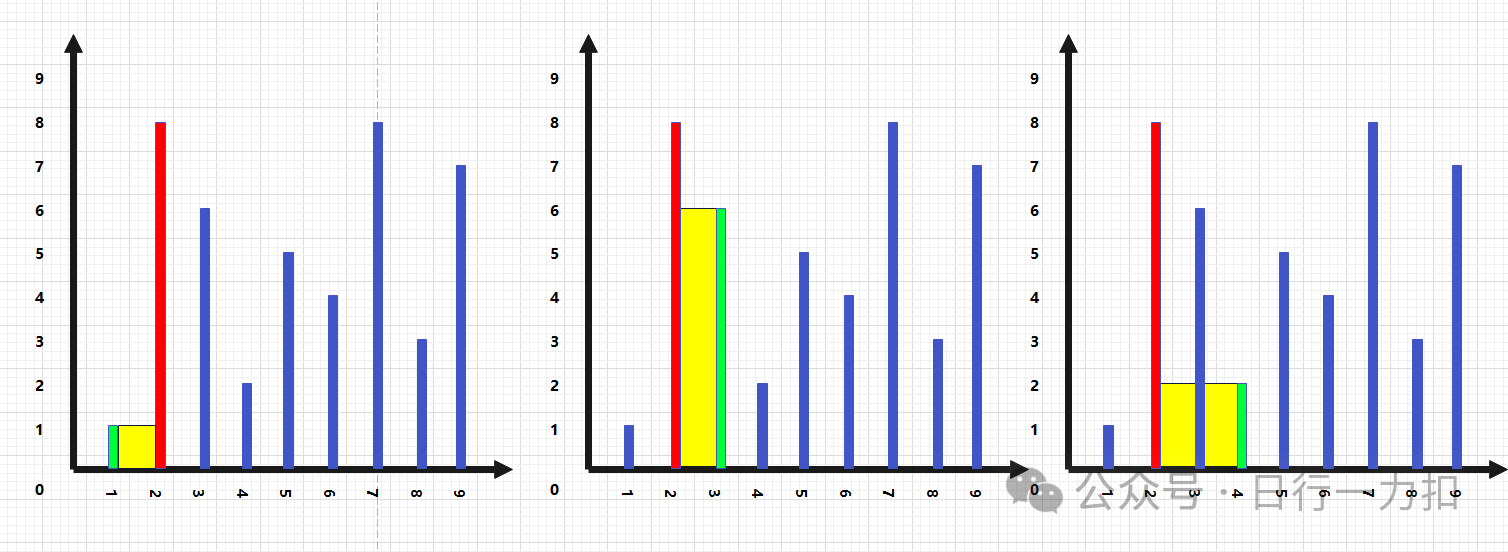
以此轮询,就可以算出每一次的最大积水量:
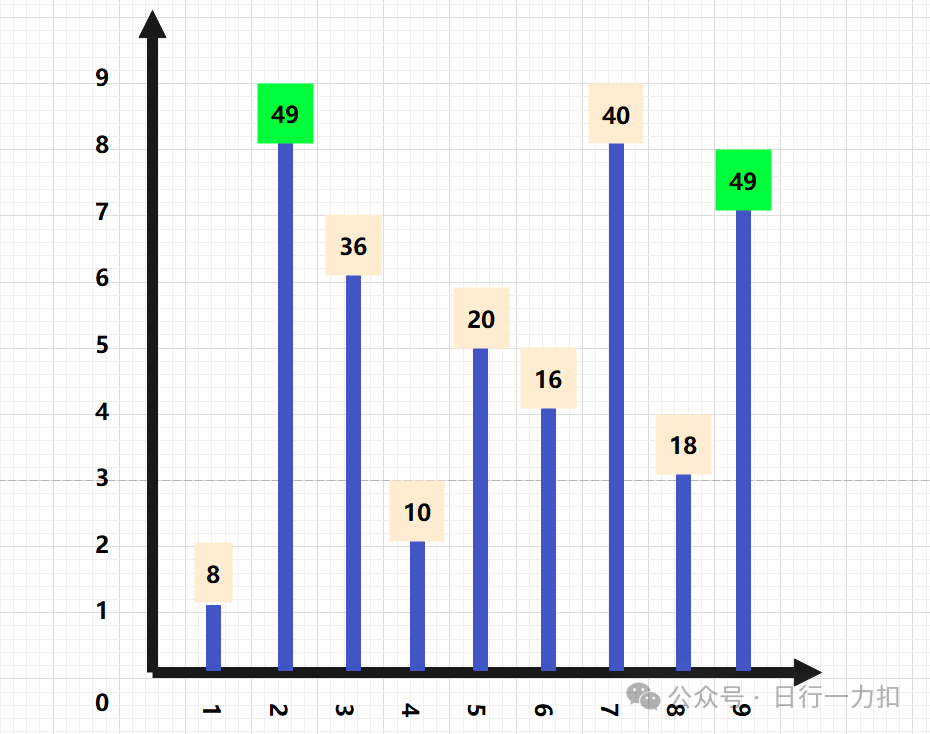
这种算法显而易见复杂度为O(n^2),效率并不高,但是起码我们能够解决问题,在能够解决问题的基础上,我们再看怎么优化。代码如下:
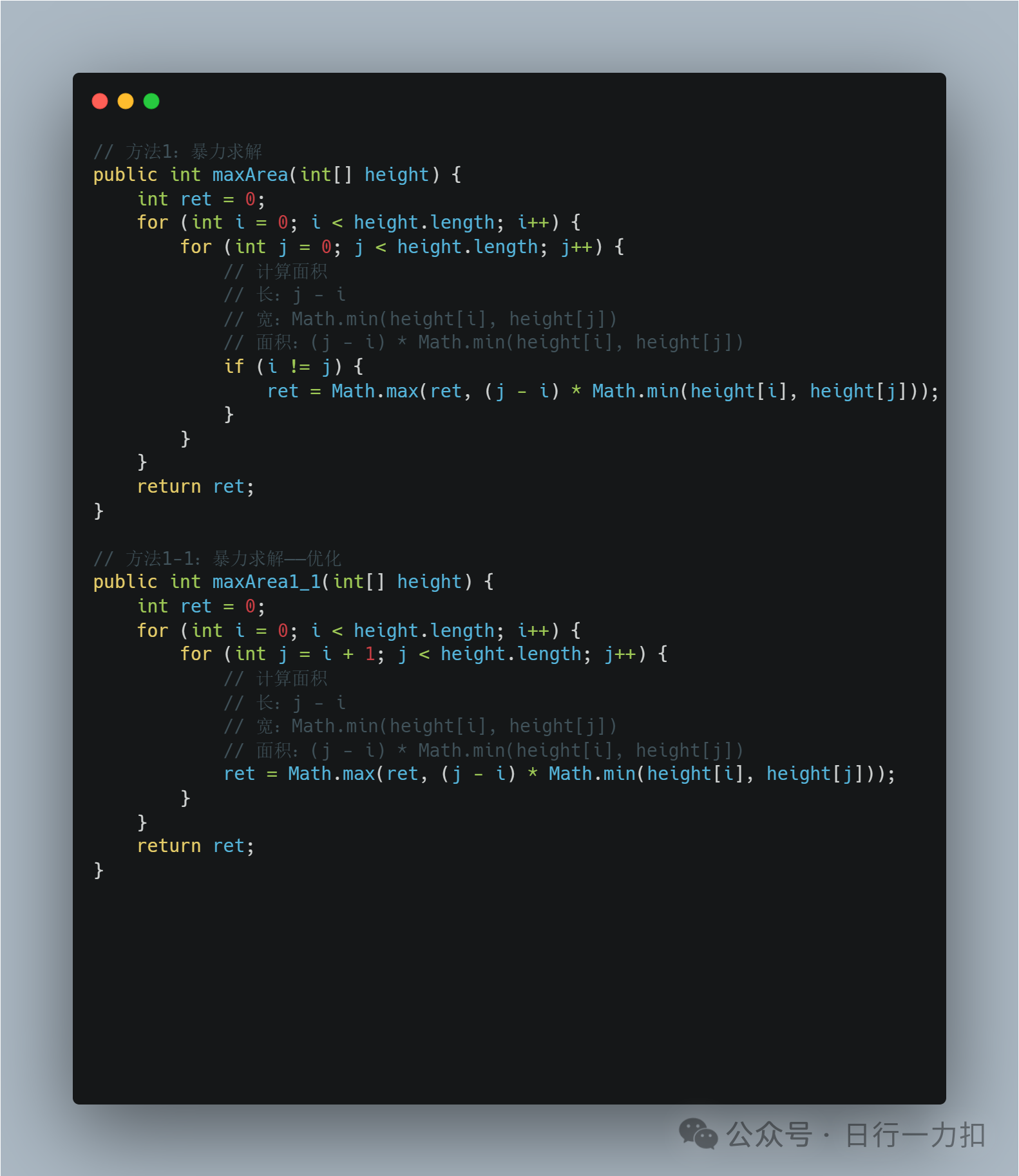
// 方法1:暴力求解public int maxArea(int[] height) {int ret = 0;for (int i = 0; i < height.length; i++) {for (int j = 0; j < height.length; j++) {// 计算面积// 长:j - i// 宽:Math.min(height[i], height[j])// 面积:(j - i) * Math.min(height[i], height[j])if (i != j) {ret = Math.max(ret, (j - i) * Math.min(height[i], height[j]));}}}return ret;}下图是我们采用上述方式的搜索空间:
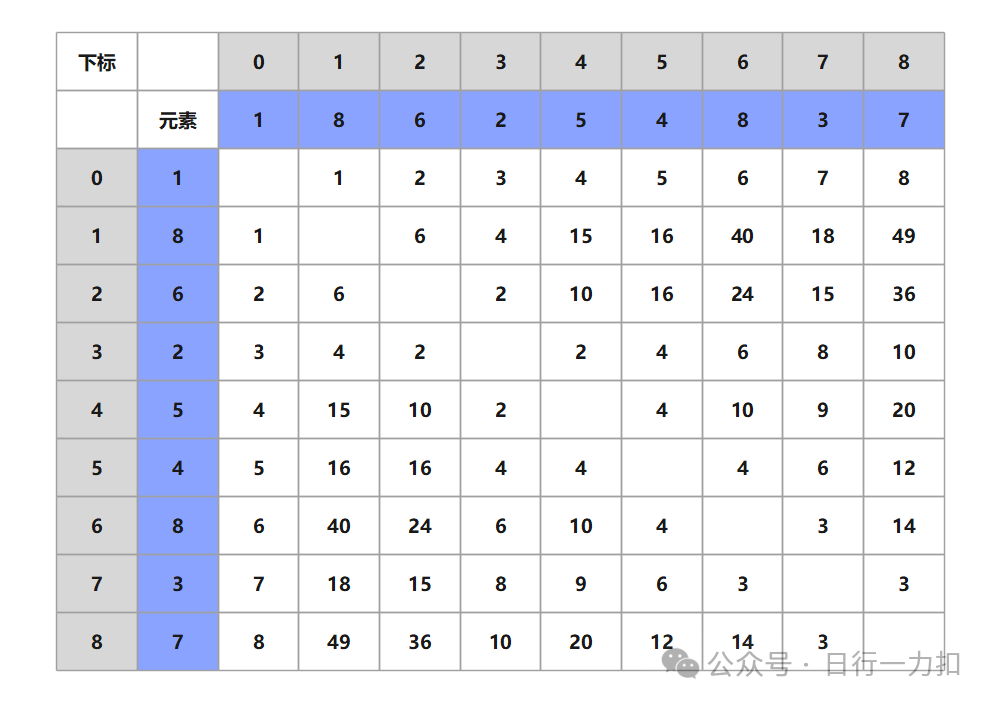
可以很明显的看到,这个是对称的,那就可以在我们在计算时内层循环可以从当前的外层循环开始遍历到结尾。如下:
// 方法1-1:暴力求解public int maxArea1_1(int[] height) {int ret = 0;for (int i = 0; i < height.length; i++) {for (int j = i + 1; j < height.length; j++) {// 计算面积// 长:j - i// 宽:Math.min(height[i], height[j])// 面积:(j - i) * Math.min(height[i], height[j])ret = Math.max(ret, (j - i) * Math.min(height[i], height[j]));}}return ret;}就将搜索空间变成如下格式:
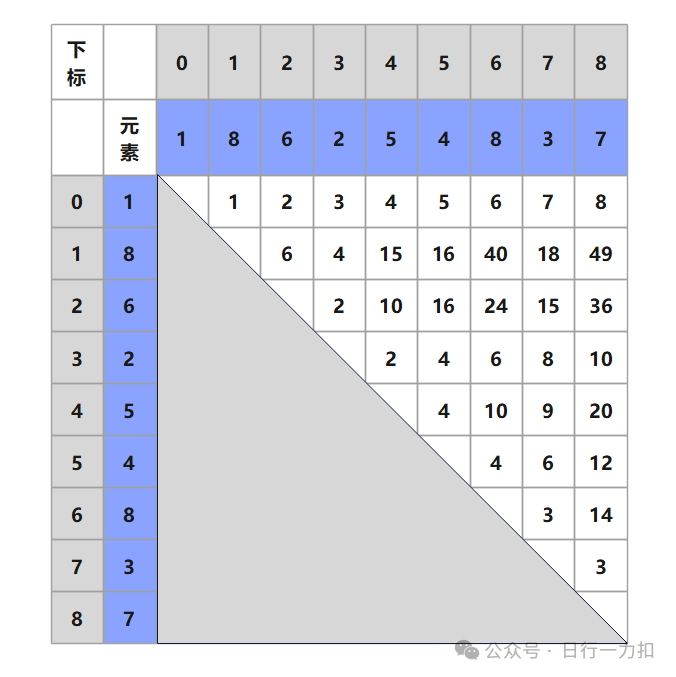
但是还是会超时的。所有我们现在看怎么用更巧妙的办法。
2.2 思路二——双指针
首先我们假设有两个指针:left和right,left指向数组的第一个元素,right指向数组的最后一个元素,这样是不是就代表了我们的两个指针包含了全部的可能储水的搜索范围(因为left与right可以移动),即left=0,right=height.length() - 1。如下:

那我们的目的就是在这个范围内怎么最快的找到题目要求的最大储水量,也就是找到对应的left与right,
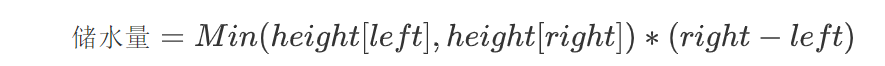
因为根据上式可以看出储水量仅仅受两个变量left与right决定。
-
Tips:对于我们需要求出的解,不妨列出公式查看决定它的因素有哪些,假如我们要求A=B与C的某种运算,就尝试找到B与C的决定因素,比如B=D*F,C=G+H,就这样递归找到问题本质的决定因素,那么我们就可以知道A本质上是由D,F,G,H决定的。然后就可以对D,F,G,H进一步分析。
因此我们就需要找到合适的right与left,而left的初始位置为0,决定了它移动的范围为[0, height.length() - 1],而right的初始位置为height.length() - 1,决定了它移动的范围为[height.length() - 1, 0]。而在移动的过程中如果left == right那么肯定是表示结束遍历了,那么走过的步骤里肯定有最大储水量的解(因为我们是在所有的解空间里查找的,当left等于right时解空间为空集,说明我们已经走过了整个解空间)。
现在我们需要思考的就是left与right 在每一步怎么动,它的运动逻辑是什么?
对于这个问题,我们还是按照刚才的步骤,先找出left和right的解空间:
-
对于left——两种状态
-
保持不动
-
+1 变大
-
-
对于right——两种状态
-
保持不动
-
-1 变小
-
保持不动自然不用说,它没有再进一步探讨的必要因为对于结果的影响不变。而对于+1与-1操作,就需要探讨它对于结果的影响。
对于left的+1操作,还存在两种可能的状态:
-
+1后left指向的值height[left]变大 -
+1后left指向的值height[left]变小
对于right的-1操作,还存在两种可能的状态:
-
-1后left指向的值height[left]变大 -
-1后left指向的值height[left]变小
现在再看一眼决定结果的公式:
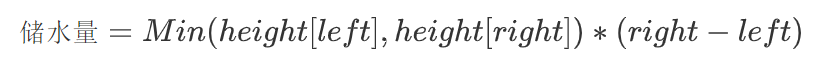
我们可以发现有一个Min函数的影响,虽然本质上还是left和right对结果的影响,但是因为left与right值决定了height[left]和height[right]的值,并且height[left]和height[right]的值决定了Min函数后的值,而最终的结果是来自于Min(height[left], height[right])和 (right - left) 。文字描述可能稍显空洞,请看下图:
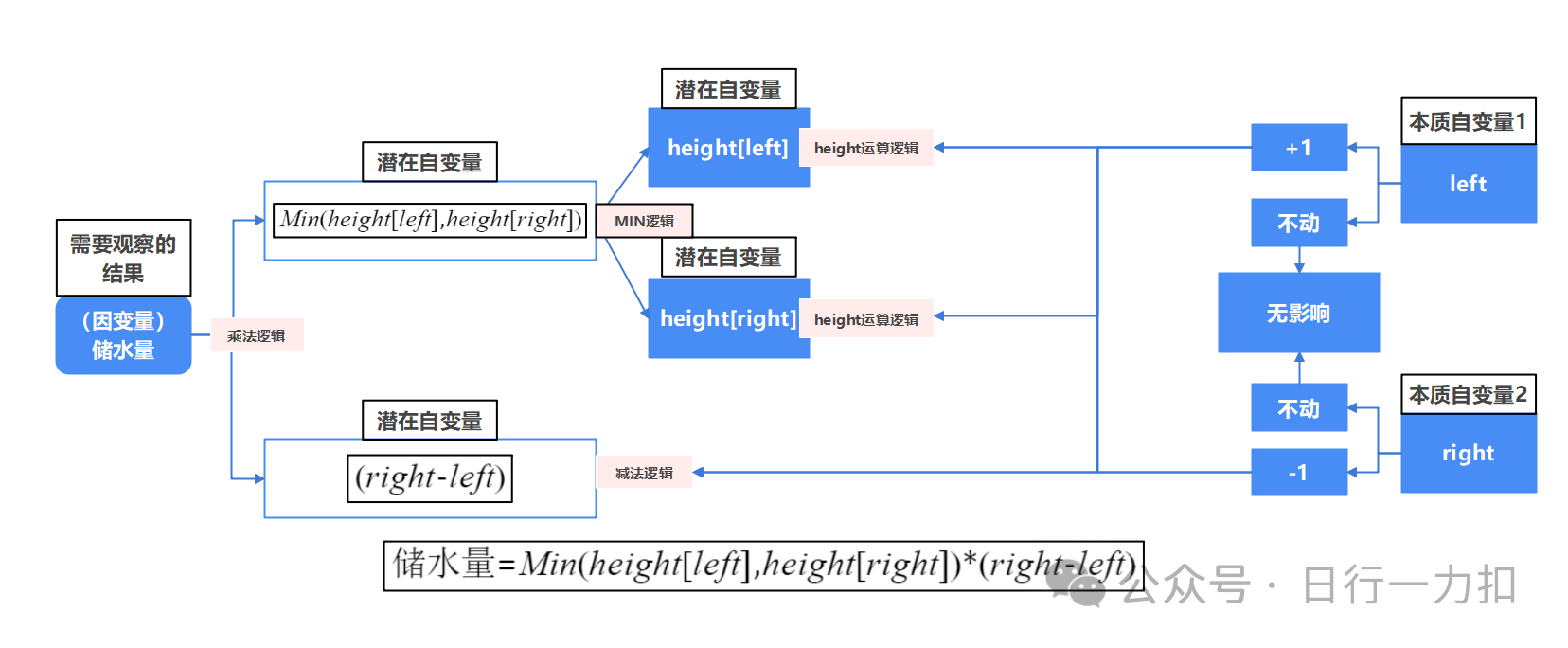
根据上图我们可以知道我们现在要倒推查看对于left的+1操作和对于right的-1操作对height和min以及right-left的影响。对right-left的影响很显而易见:
-
left+1整个值
right-left减小1 -
right-1整个值
right-left减小1
所有我们主要看对于height和min逻辑的影响:
-
对于left而言,+1操作可以分为两种大情况
-
height[left+1] > height[left]
-
A:如果原先height[left] > height[right]那么移动后对于储水量而言肯定变小,因为储水量变化等于移动后的储水量减去移动前的储水量,公式如下:
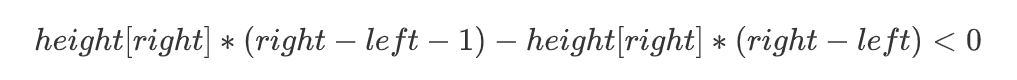
-
B:如果原先height[left] <= height[right]那么移动后对于储水量而言可能变大可能变小,是不能确定大小的
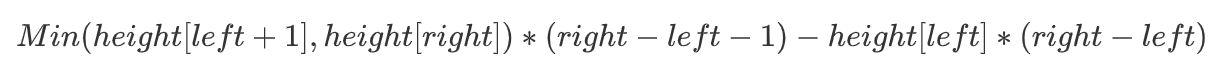
-
-
height[left+1] <= height[left]
-
C:如果原先height[left] > height[right]那么移动后对于储水量而言是肯定变小
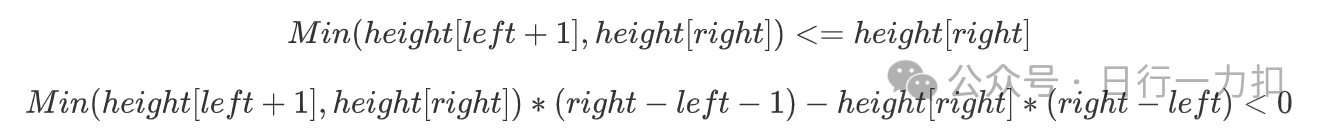
-
D:如果原先height[left] <= height[right]那么移动后对于储水量而言是肯定变小

-
-
对于right而言,+1操作也可以分为两种大情况
-
height[right-1] > height[right]
-
E:如果原先height[right] > height[left]那么移动后对于储水量而言肯定变小
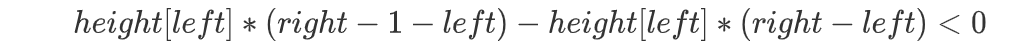
-
F:如果原先height[right] <= height[left]那么移动后对于储水量而言可能变大可能变小
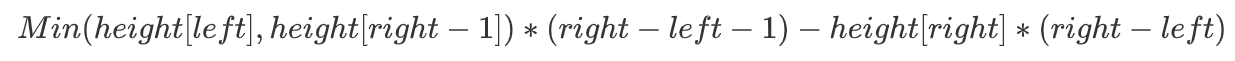
-
-
height[right-1] <= height[right]
-
G:如果原先height[right] > height[left]那么移动后对于储水量而言肯定变小
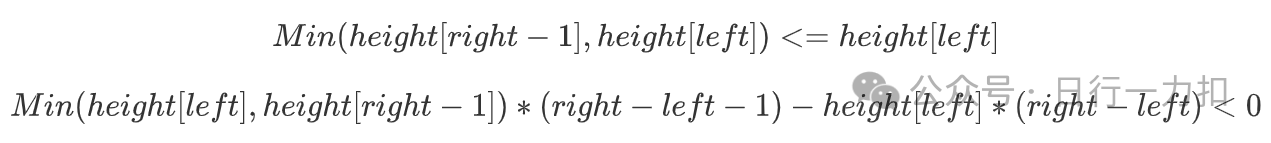
-
H:如果原先height[right] <= height[left]那么移动后结对于储水量而言肯定变小
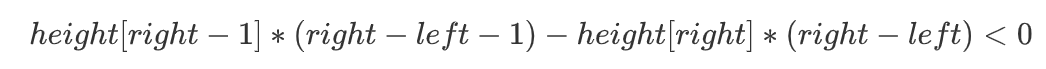
-
由于我们的目的是找到最大的解,也就是说我们肯定不想通过移动让值变小。而经过上面的论证,我们可以发现是有一定的规律的,对于height[left]与height[right],
-
如果我们移动大的一边,也就是对应上述{A, C, E, G},结果肯定是变小的
-
而如果移动小(或相等)的一边,也就是对应上述 {B, D, F, H}:
-
如果要移动的位置大于当前位置,对应 {B, F}, 那得到的结果可能变大可能变小。
-
如果要移动的位置小于当前位置,对应 {F, H}, 那得到的结果肯定变小。
-
所以分析到这里我们就可以知道两个指针left与right的运动规律了。如果我们想要的到最大的结果,那么就得让指针按照上述{B,F}的方向走,也就是必须得移动小的一边,虽然说包含了{B, D, F, H},但起码有变大的可能。。这样当两个指针从两头走到碰面,就可以保证经历了所有的可能变大的结果,其中最大的值就是找到的最大储水量。
所以解题思路为:
-
左右指针指向数组头尾
-
移动指向的值较小的指针,计算并保存最大值
-
得到结果
看到这里肯定有些人还有疑惑,为什么这样是正确的?凭什么你说这样就能考虑了所有的情况?
解释:开始的left与right指向两端,如之前给过的图一样:
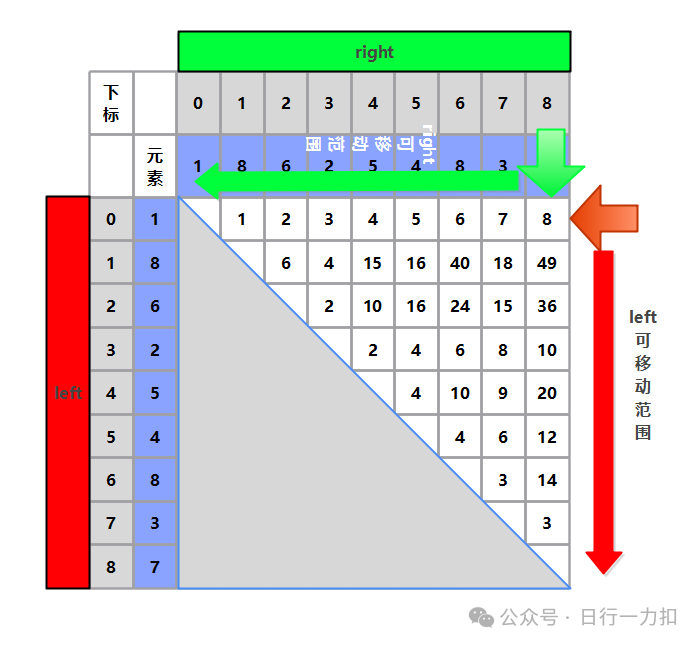
它是能包含所有解的,因为right和left的移动范围是包含了整个解空间的,而我们的上述分析只需要走 {B, D, F, G}方向的路径,是相当于用数学的方法进行了走向的优化,减少了不必要的行程。而最终当right于left碰面就退出,那时候已经走到了边界,继续再向下搜索是会得到重复的结果的,可以执行,但没必要。以题目中的测试用例为例子,其搜索过程是如下的:
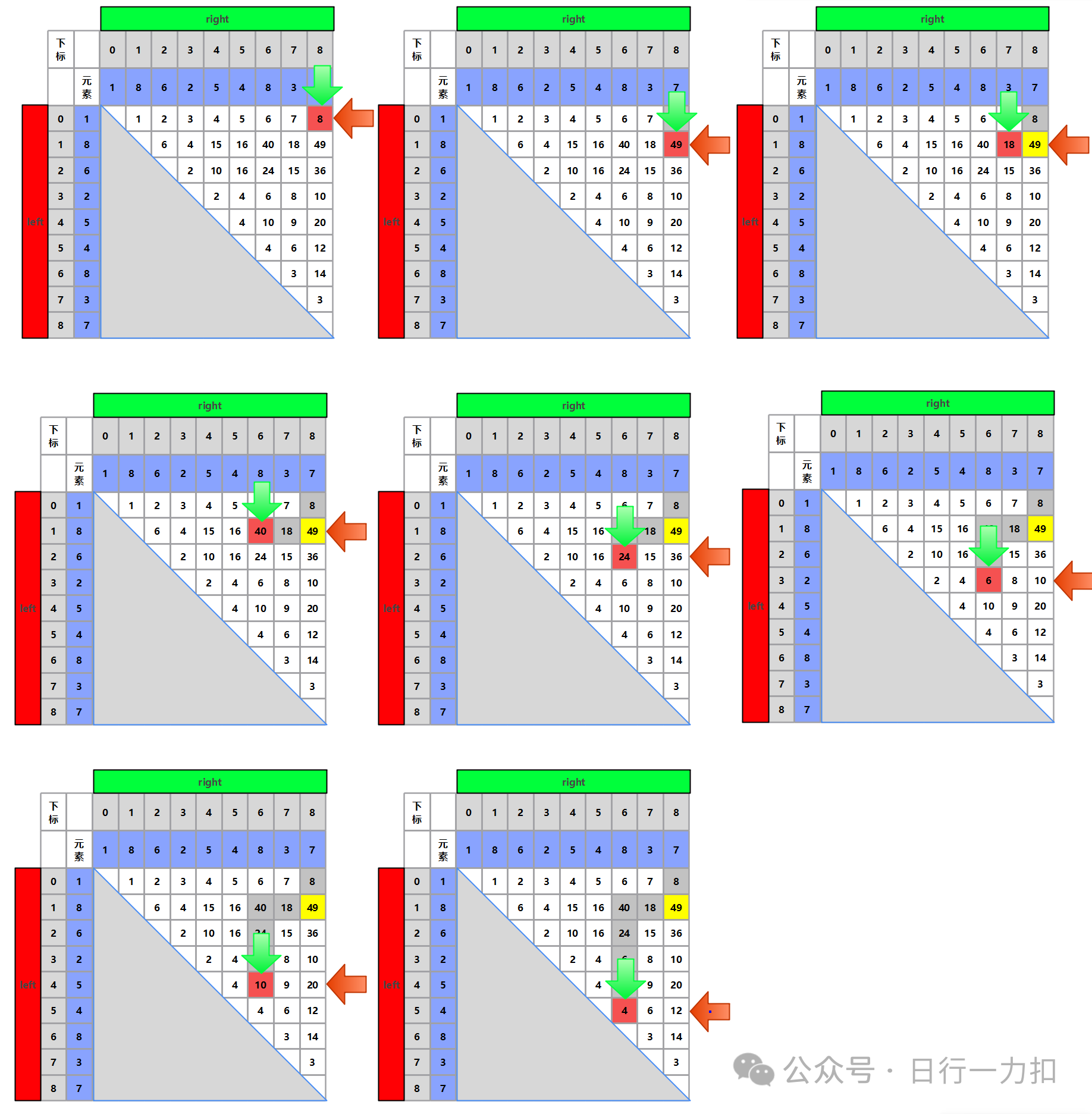
如果继续往下搜索,那么会得到如下:
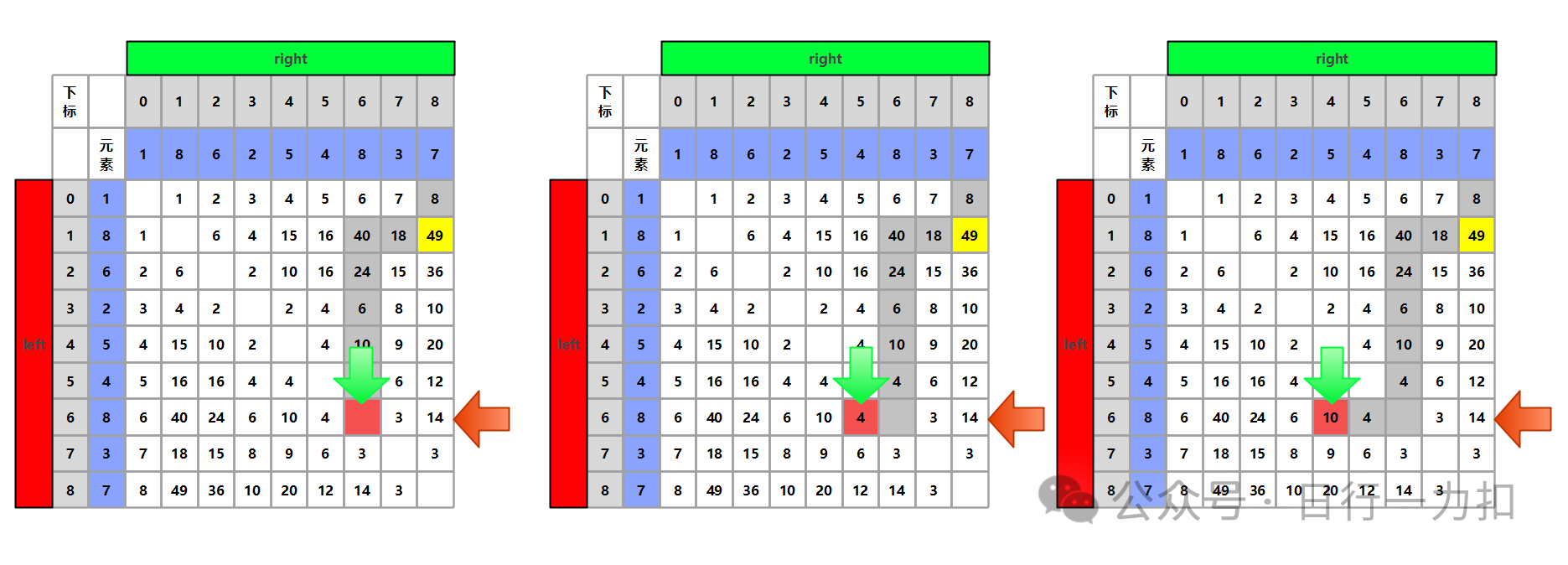
最终的搜索路线为:
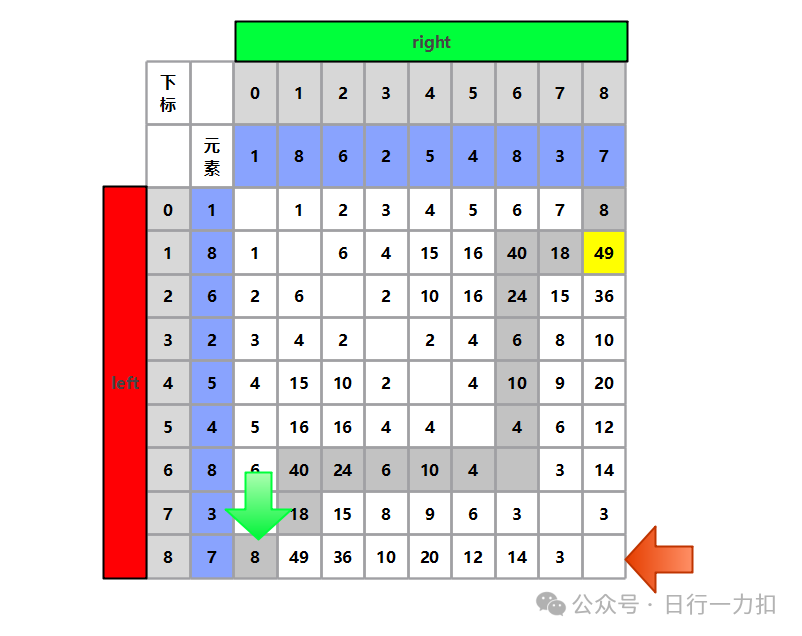
可以看到无非就是重复了一次right > left的路线。
现在着重讲一下为什么我这样走就能找到最优解
首先,假设我们现在在初始位置:
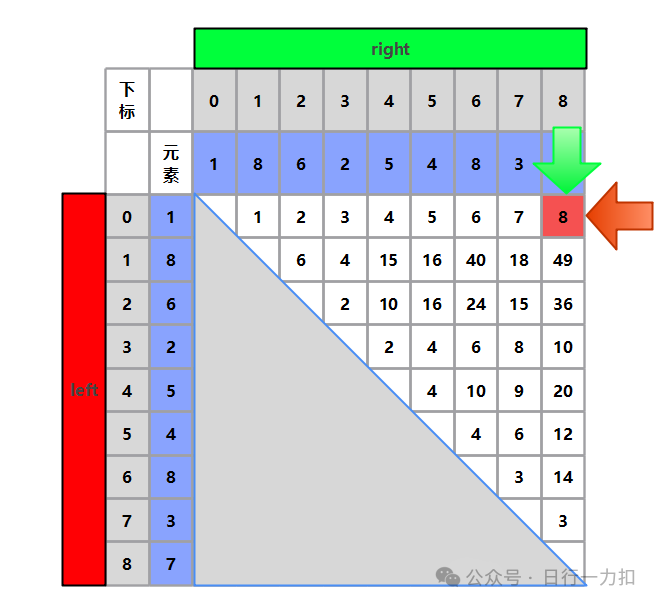
根据前面介绍的公式,我们可以知道,此时决定储水量的看left和right指向的较小的值,因为此时height[left]=1,height[right]=7,较小的值为height[left]=1,理论上是需要将left+1。而如果我们在这个位置左移right,也就是不断将right - 1,那么储水量肯定是不会大于当前值的。因为 Min(height[left], height[right])中较小的值肯定是小于等于目前的值,换句话说,就是Min(height[left],height[right])中现在最小的是height[left],如果不断变小right,则变化的值为height[right]。而这个变化的height[right]
-
要么大于height[left],则Min(height[left],height[right])仍然为height[left]
-
要么等于或者小于height[left],则Min(height[left],height[right])等于height[right],仍然小于等于height[left]
所以储水量肯定不会大于当前值,所以就可以排除如下图黄色部分:
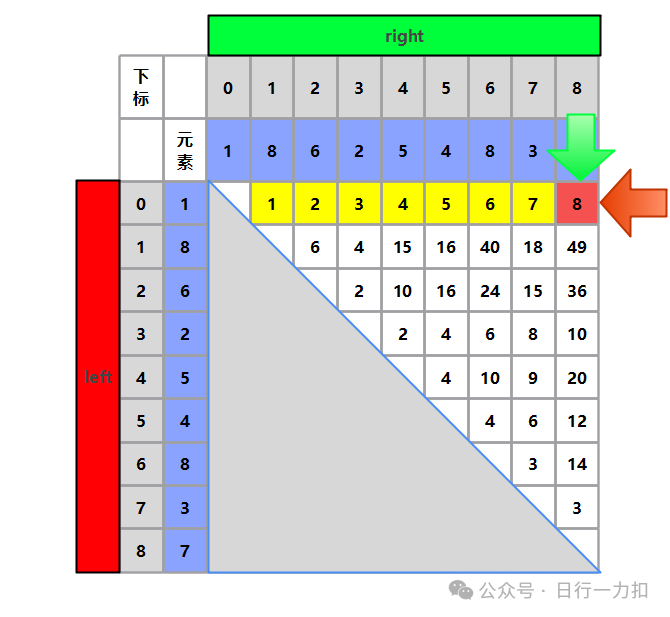
当走到第二个位置同理,因为height[left] > height[right],所以需要动right,将right - 1。如果我们假设让left移动,就是让left不断加1,那么储水量肯定也是不会大于当前值的。同上,因为 Min(height[left], height[right])中较小的值肯定是小于等于目前的值,换句话说,就是Min(height[left],height[right])中现在最小的是height[right],如果不断变大left,则变化的值为height[left]。而这个变化的height[left]
-
要么大于height[right],则Min(height[left],height[right])仍然为height[right]
-
要么等于或者小于height[right],则Min(height[left],height[right])等于height[left],仍然小于等于height[right]的
得到的储水量肯定不会大于当前值,所以就可以排除如下图紫色部分:
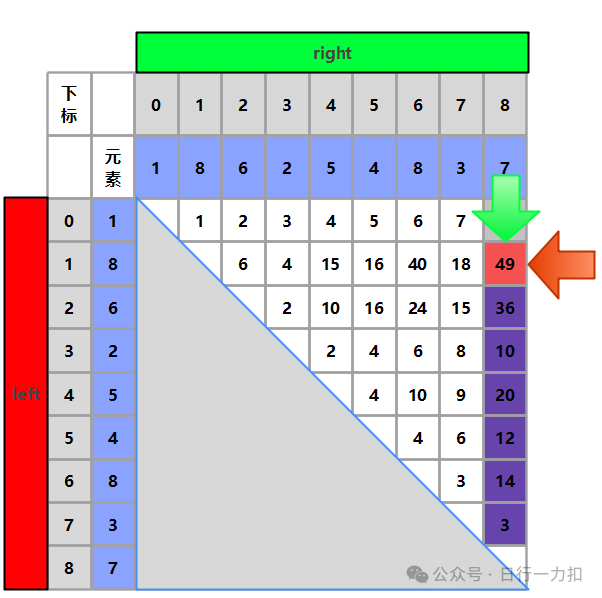
同理按照上述步骤,后续过程如下,紫色部分为每一次的排除部分:
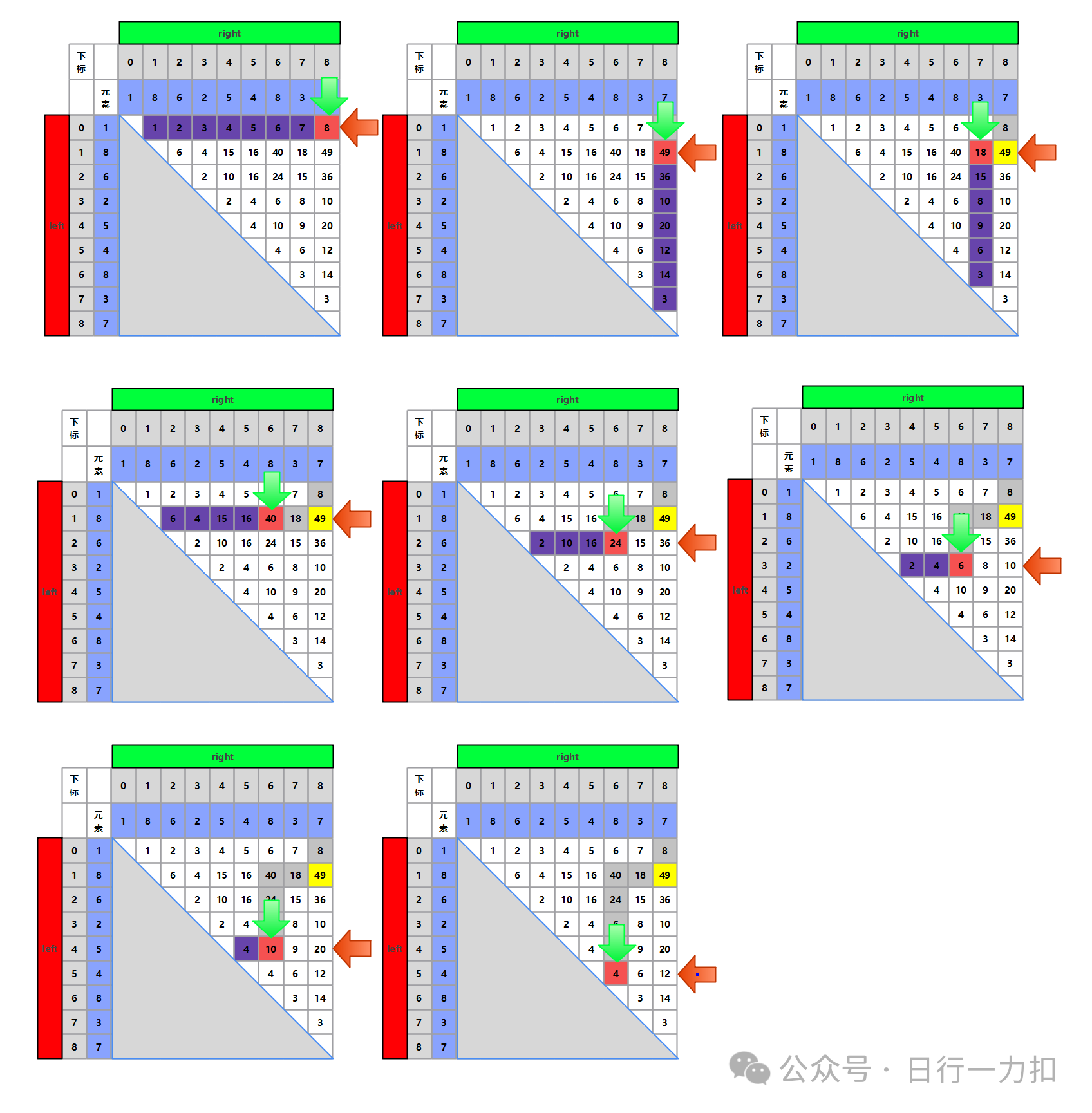
总结
其实我们每一步的搜寻都是尝试将部分可能解基于我们前面推理的数学公式排除掉了,从开始的暴力枚举到排除一半可行解,再到双指针每次搜寻排除某一行或者某一列的解,这个过程其实就是不断优化的过程。
3. 代码实现
3.1 思路一——暴力求解
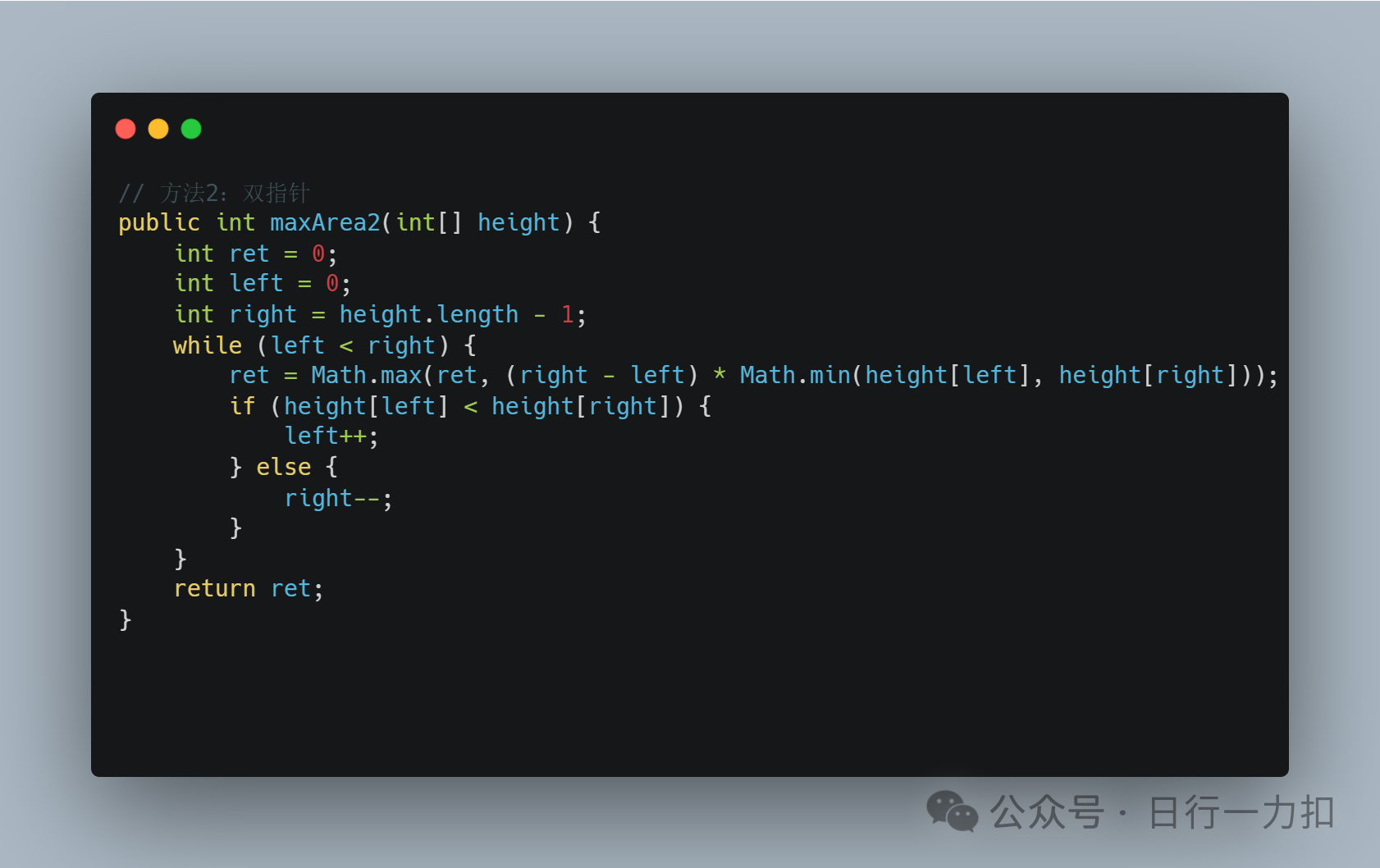
3.2 思路二——双指针
4. 运行结果
方法一
会报超时
方法二
5. 相关复杂度分析
方法一
暴力枚举所有可行解,需要走所有的解空间,所以时间复杂度为O(n^2),空间复杂度为O(1)
方法二
-
时间复杂度:O(N),双指针总计最多遍历整个数组一次。
-
空间复杂度:O(1),只需要额外的常数级别的空间。
个人公众号:推出最新高质量文章:


)
MybatisPlus启动流程)
)
)




![[145] 二叉树的后序遍历 js](http://pic.xiahunao.cn/[145] 二叉树的后序遍历 js)

)

![[office] 怎么在Excel2003菜单栏自定义一个选项卡 #其他#微信#知识分享](http://pic.xiahunao.cn/[office] 怎么在Excel2003菜单栏自定义一个选项卡 #其他#微信#知识分享)




