- 什么是排序算法
- 冒泡排序
- 选择排序
- 插入排序
- 快速排序
- 归并排序(Merge Sort)
- 思想
- 实现
- 测试
- 分析
- 动画
- 快速排序 (Quick Sort)
- 思想
- 实现
- 测试
- 分析
- 动画
- 思考:快排和归并用的都是分治思想,递推公式和递归代码也非常相似,那它们的区别在哪里呢 ?
- 希尔排序(Shell Sort)
- 思想
- 过程
- 实现
- 测试
- 分析
- 动画
- 堆排序(Heap Sort)
- 堆的定义
- 思想
- 实现
- 测试
- 分析
- 动画
- 排序算法的复杂性对比
什么是排序算法
排序算法是计算机科学中常用的一种算法,用于将一组元素按照特定的顺序进行排列。
排序算法是一种针对数据集合进行排序的算法。
排序算法通常采用比较和交换的方式来对数据进行排序,使得数据按照一定规则排列。
排序算法在计算机科学中有着重要的应用,例如在数据检索、数据分析、数据压缩等领域都需要使用排序算法。
排序算法可以分为内部排序和外部排序两种。
内部排序是指所有需要排序的数据能够一次性存放在计算机的内存中进行排序的过程。
而外部排序则是指需要对不适合全部存储在内存中的大规模数据进行排序,通过将数据分成多个可以全部存储在内存中的部分进行排序,最终再合并成一个完整的排序结果。
以下是几种常见的排序算法:
-
冒泡排序(Bubble Sort):该算法通过相邻元素之间的比较和交换来进行排序,每次循环将最大的元素逐渐移到数组的最后。
-
插入排序(Insertion Sort):该算法类似于整理扑克牌的过程,从未排序的部分选择一个元素插入到已排序的部分,直到所有元素都被插入到正确的位置。
-
选择排序(Selection Sort):该算法每次从未排序的部分选择最小(或最大)的元素,并与当前位置进行交换,重复这个过程直到数组完全有序。
-
快速排序(Quick Sort):该算法使用分治法的思想,首先选择一个基准元素,然后将其他元素分为两个子数组,小于基准的放左边,大于基准的放右边,然后递归地对子数组进行排序。
-
归并排序(Merge Sort):该算法采用分治法的思想,将待排序的数组不断地二分,直到每个子数组只包含一个元素,然后将这些子数组合并成一个有序的数组。
以上仅是排序算法中的几种常见算法,每种算法的时间复杂度、空间复杂度和稳定性等特点各不相同,选择适合具体场景的排序算法能够提高排序效率。
冒泡排序
冒泡排序是最基本的排序算法,它重复地走访过要排序的数列,一次比较两个元素,如果它们的顺序错误就把它们交换过来。
function bubbleSort(arr) {var len = arr.length;for (var i = 0; i < len - 1; i++) {for (var j = 0; j < len - i - 1; j++) {if (arr[j] > arr[j + 1]) {var temp = arr[j];arr[j] = arr[j + 1];arr[j + 1] = temp;}}}return arr;
}
选择排序
选择排序也是比较简单的一种排序算法,它的主要思想是在未排序的数列中找到最小元素,并把它放到已排序的数列的末尾。
function selectionSort(arr) {var len = arr.length;for (var i = 0; i < len - 1; i++) {var minIndex = i;for (var j = i + 1; j < len; j++) {if (arr[j] < arr[minIndex]) {minIndex = j;}}if (minIndex !== i) {var temp = arr[i];arr[i] = arr[minIndex];arr[minIndex] = temp;}}return arr;
}
插入排序
插入排序的基本思想是将待排序的数列分成已排序和未排序两部分,每次从未排序部分取出一个元素,然后将它插入到已排序部分的合适位置。
function insertionSort(arr) {var len = arr.length;for (var i = 1; i < len; i++) {var j = i;var temp = arr[i];while (j > 0 && arr[j - 1] > temp) {arr[j] = arr[j - 1];j--;}arr[j] = temp;}return arr;
}
快速排序
快速排序是一种比较高效的排序算法,它的主要思想是选择一个基准元素,然后把比它小的元素放在左边,比它大的元素放在右边,然后对左右两部分分别进行递归排序。
function quickSort(arr, left, right) {if (left < right) {var pivot = partition(arr, left, right);quickSort(arr, left, pivot - 1);quickSort(arr, pivot + 1, right);}return arr;
}function partition(arr, left, right) {var pivot = arr[left];var i = left;var j = right;while (i < j) {while (arr[j] >= pivot && i < j) {j--;}arr[i] = arr[j];while (arr[i] <= pivot && i < j) {i++;}arr[j] = arr[i];}arr[i] = pivot;return i;
}
以上是几种常见的 JavaScript 排序算法的手写实现,它们在实际应用中都有着广泛的应用。
更多详细内容,请微信搜索“前端爱好者“, 戳我 查看 。
归并排序(Merge Sort)
思想
排序一个数组,我们先把数组从中间分成前后两部分,然后对前后两部分分别排序,再将排好序的两部分合并在一起,这样整个数组就都有序了。
归并排序采用的是 分治思想。
分治,顾名思义,就是分而治之,将一个大问题分解成小的子问题来解决。小的子问题解决了,大问题也就解决了。
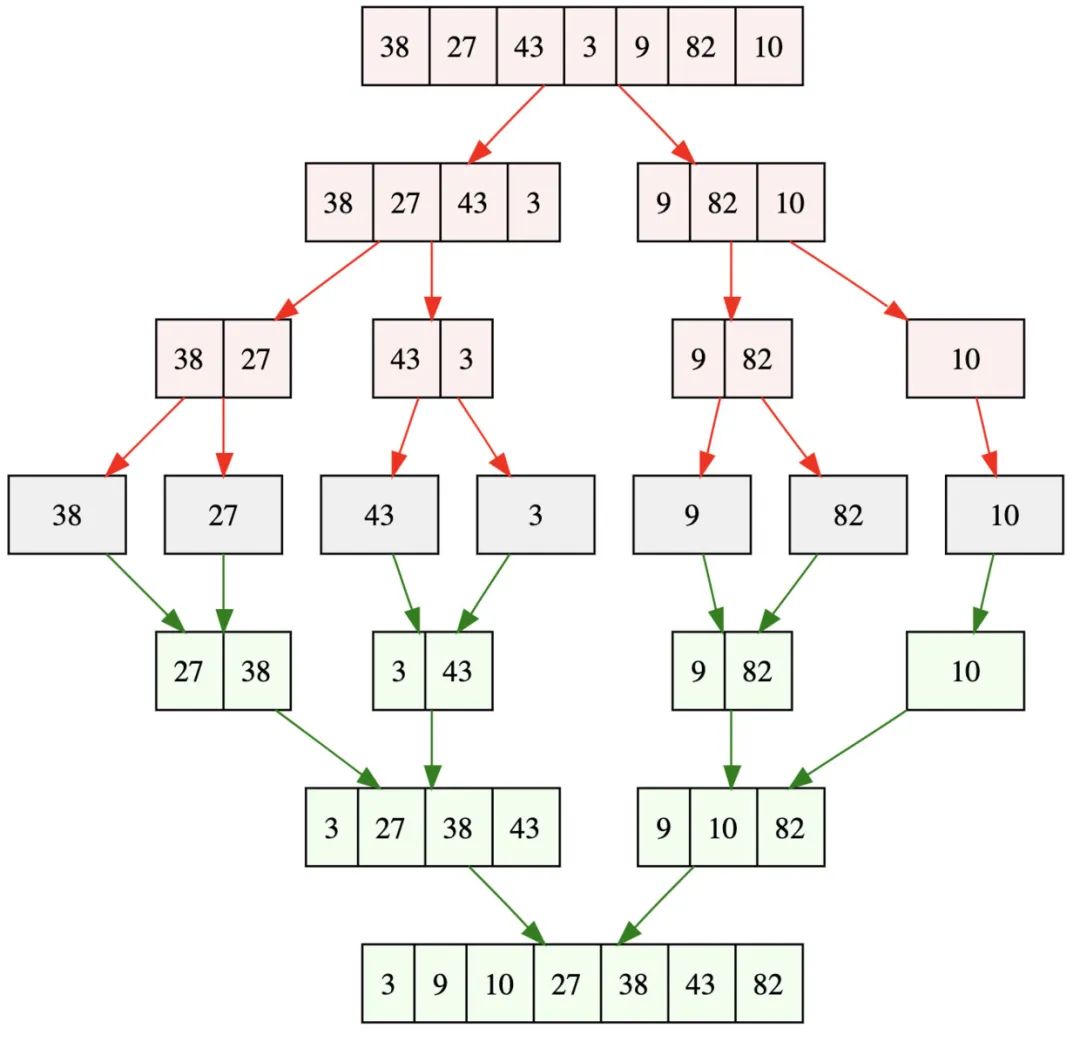
注:x >> 1 是位运算中的右移运算,表示右移一位,等同于 x 除以 2 再取整,即 x >> 1 === Math.floor(x / 2) 。
实现
const mergeSort = arr => {//采用自上而下的递归方法const len = arr.length;if (len < 2) {return arr;}// length >> 1 和 Math.floor(len / 2) 等价let middle = Math.floor(len / 2),left = arr.slice(0, middle),right = arr.slice(middle); // 拆分为两个子数组return merge(mergeSort(left), mergeSort(right));
};
const merge = (left, right) => {const result = [];while (left.length && right.length) {// 注意: 判断的条件是小于或等于,如果只是小于,那么排序将不稳定.if (left[0] <= right[0]) {result.push(left.shift());} else {result.push(right.shift());}}while (left.length) result.push(left.shift());while (right.length) result.push(right.shift());return result;
};
测试
// 测试
const arr = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48];
console.time('归并排序耗时');
console.log('arr :', mergeSort(arr));
console.timeEnd('归并排序耗时');
// arr : [2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]
// 归并排序耗时: 0.739990234375ms
分析
第一,归并排序是原地排序算法吗 ?
这是因为归并排序的合并函数,在合并两个有序数组为一个有序数组时,需要借助额外的存储空间。
实际上,尽管每次合并操作都需要申请额外的内存空间,但在合并完成之后,临时开辟的内存空间就被释放掉了。在任意时刻,CPU 只会有一个函数在执行,也就只会有一个临时的内存空间在使用。临时内存空间最大也不会超过 n 个数据的大小,所以空间复杂度是 O(n)。
所以,归并排序不是原地排序算法。
第二,归并排序是稳定的排序算法吗 ?
merge 方法里面的 left[0] <= right[0] ,保证了值相同的元素,在合并前后的先后顺序不变。
归并排序是一种稳定的排序方法。
第三,归并排序的时间复杂度是多少 ?
从效率上看,归并排序可算是排序算法中的佼佼者。假设数组长度为 n,那么拆分数组共需 logn 步, 又每步都是一个普通的合并子数组的过程,时间复杂度为 O(n),故其综合时间复杂度为 O(nlogn)。
最佳情况:T(n) = O(nlogn)。
最差情况:T(n) = O(nlogn)。
平均情况:T(n) = O(nlogn)。
动画
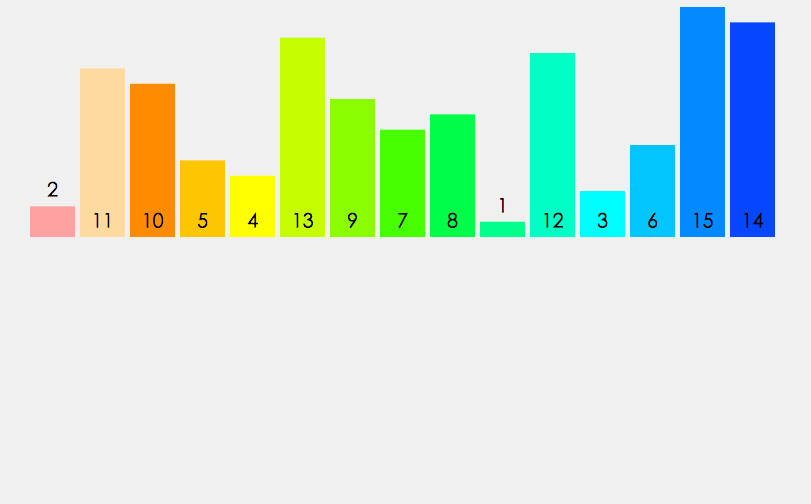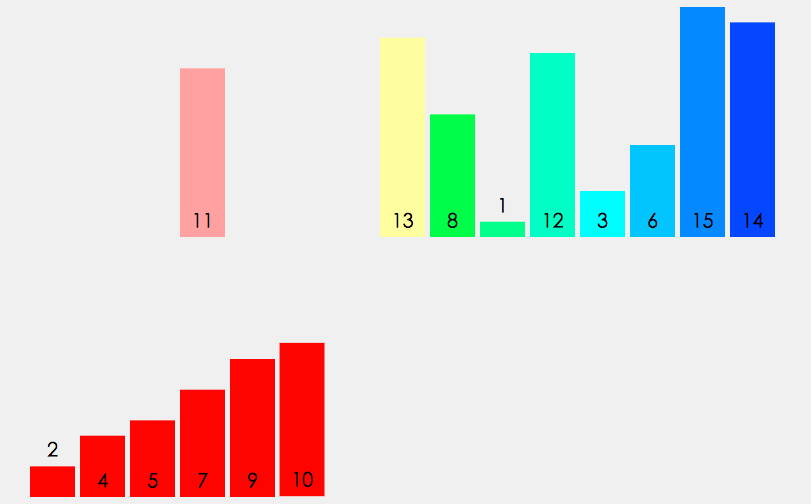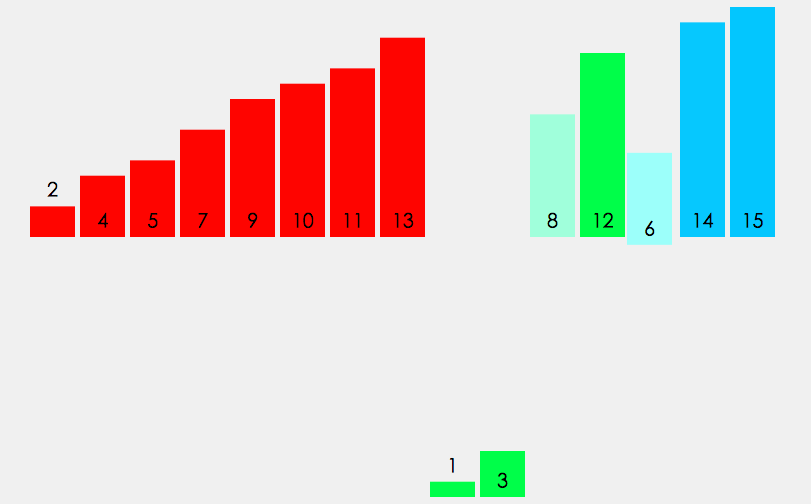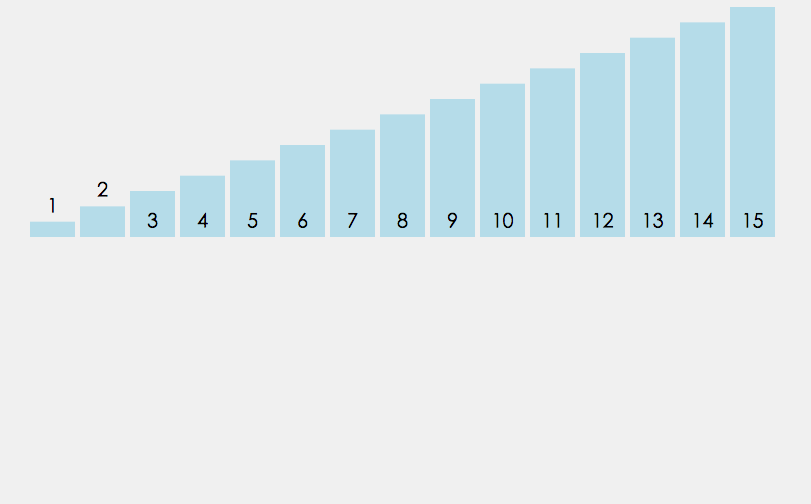
快速排序 (Quick Sort)
快速排序的特点就是快,而且效率高!它是处理大数据最快的排序算法之一。
思想
先找到一个基准点(一般指数组的中部),然后数组被该基准点分为两部分,依次与该基准点数据比较,如果比它小,放左边;反之,放右边。
左右分别用一个空数组去存储比较后的数据。
最后递归执行上述操作,直到数组长度 <= 1;
特点:快速,常用。
缺点:需要另外声明两个数组,浪费了内存空间资源。
实现
方法一:
const quickSort1 = arr => {if (arr.length <= 1) {return arr;}//取基准点const midIndex = Math.floor(arr.length / 2);//取基准点的值,splice(index,1) 则返回的是含有被删除的元素的数组。const valArr = arr.splice(midIndex, 1);const midIndexVal = valArr[0];const left = []; //存放比基准点小的数组const right = []; //存放比基准点大的数组//遍历数组,进行判断分配for (let i = 0; i < arr.length; i++) {if (arr[i] < midIndexVal) {left.push(arr[i]); //比基准点小的放在左边数组} else {right.push(arr[i]); //比基准点大的放在右边数组}}//递归执行以上操作,对左右两个数组进行操作,直到数组长度为 <= 1return quickSort1(left).concat(midIndexVal, quickSort1(right));
};
const array2 = [5, 4, 3, 2, 1];
console.log('quickSort1 ', quickSort1(array2));
// quickSort1: [1, 2, 3, 4, 5]
方法二:
// 快速排序
const quickSort = (arr, left, right) => {let len = arr.length,partitionIndex;left = typeof left != 'number' ? 0 : left;right = typeof right != 'number' ? len - 1 : right;if (left < right) {partitionIndex = partition(arr, left, right);quickSort(arr, left, partitionIndex - 1);quickSort(arr, partitionIndex + 1, right);}return arr;
};
const partition = (arr, left, right) => {//分区操作let pivot = left, //设定基准值(pivot)index = pivot + 1;for (let i = index; i <= right; i++) {if (arr[i] < arr[pivot]) {swap(arr, i, index);index++;}}swap(arr, pivot, index - 1);return index - 1;
};
const swap = (arr, i, j) => {let temp = arr[i];arr[i] = arr[j];arr[j] = temp;
};
测试
// 测试
const array = [5, 4, 3, 2, 1];
console.log('原始array:', array);const newArr = quickSort(array);
console.log('newArr:', newArr);
// 原始 array: [5, 4, 3, 2, 1]
// newArr: [1, 4, 3, 2, 5]
分析
第一,快速排序是原地排序算法吗 ?
因为 partition() 函数进行分区时,不需要很多额外的内存空间,所以快排是原地排序算法。
第二,快速排序是稳定的排序算法吗 ?
和选择排序相似,快速排序每次交换的元素都有可能不是相邻的,因此它有可能打破原来值为相同的元素之间的顺序。因此,快速排序并不稳定。
第三,快速排序的时间复杂度是多少 ?
极端的例子:如果数组中的数据原来已经是有序的了,比如 1,3,5,6,8。
如果我们每次选择最后一个元素作为 pivot,那每次分区得到的两个区间都是不均等的。我们需要进行大约 n 次分区操作,才能完成快排的整个过程。每次分区我们平均要扫描大约 n / 2 个元素,这种情况下,快排的时间复杂度就从 O(nlogn) 退化成了 O(n2)。
最佳情况:T(n) = O(nlogn)。
最差情况:T(n) = O(n2)。
平均情况:T(n) = O(nlogn)。
动画
思考:快排和归并用的都是分治思想,递推公式和递归代码也非常相似,那它们的区别在哪里呢 ?
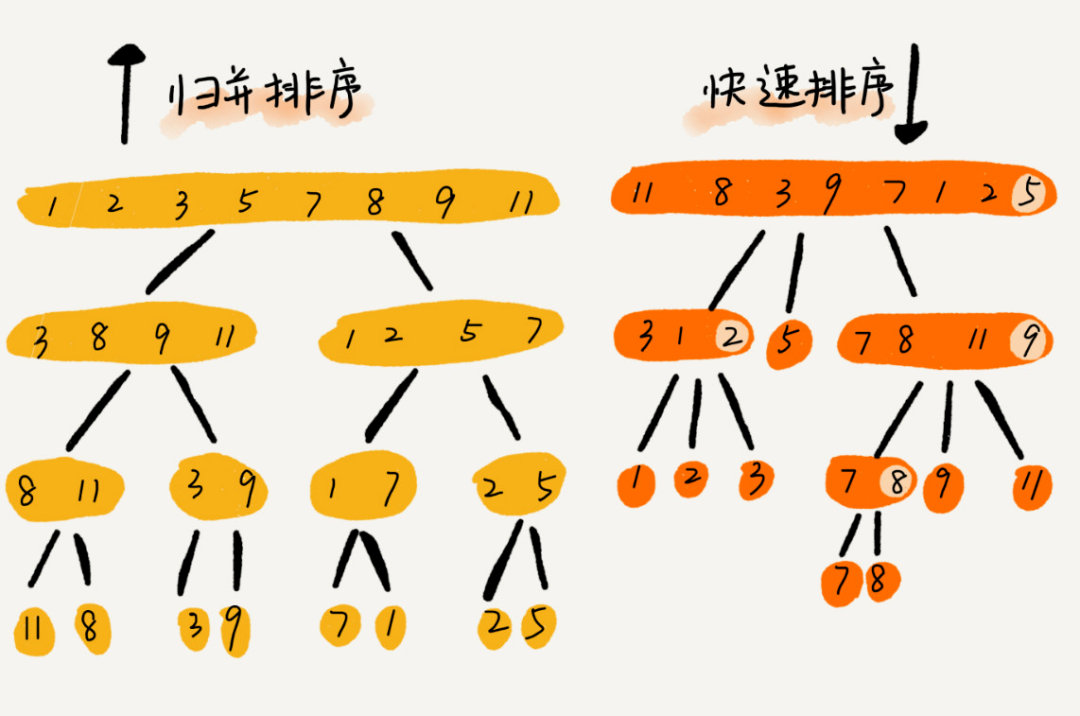
可以发现:
- 归并排序的处理过程是由下而上的,先处理子问题,然后再合并。而快排正好相反,它的处理过程是由上而下的,先分区,然后再处理子问题。
- 归并排序虽然是稳定的、时间复杂度为 O(nlogn) 的排序算法,但是它是非原地排序算法。归并之所以是非原地排序算法,主要原因是合并函数无法在原地执行。
- 快速排序通过设计巧妙的原地分区函数,可以实现原地排序,解决了归并排序占用太多内存的问题。
希尔排序(Shell Sort)
思想
先将整个待排序的记录序列分割成为若干子序列。
分别进行直接插入排序。
待整个序列中的记录基本有序时,再对全体记录进行依次直接插入排序。
过程
举个易于理解的例子:[35, 33, 42, 10, 14, 19, 27, 44],我们采取间隔 4。
创建一个位于 4 个位置间隔的所有值的虚拟子列表。
下面这些值是 { 35, 14 },{ 33, 19 },{ 42, 27 } 和 { 10, 44 }。
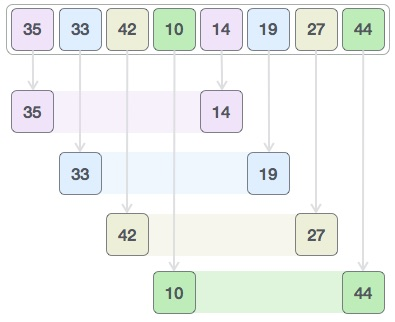
我们比较每个子列表中的值,并在原始数组中交换它们(如果需要)。
完成此步骤后,新数组应如下所示。

然后,我们采用 2 的间隔,这个间隙产生两个子列表:{ 14, 27, 35, 42 }, { 19, 10, 33, 44 }。

我们比较并交换原始数组中的值(如果需要)。完成此步骤后,数组变成:[14, 10, 27, 19, 35, 33, 42, 44],图如下所示,10 与 19 的位置互换一下。

最后,我们使用值间隔 1 对数组的其余部分进行排序,Shell sort 使用插入排序对数组进行排序。
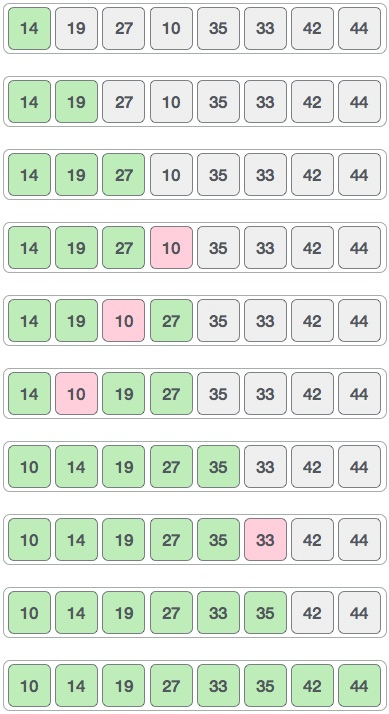
实现
const shellSort = arr => {let len = arr.length,temp,gap = 1;console.time('希尔排序耗时');while (gap < len / 3) {//动态定义间隔序列gap = gap * 3 + 1;}for (gap; gap > 0; gap = Math.floor(gap / 3)) {for (let i = gap; i < len; i++) {temp = arr[i];let j = i - gap;for (; j >= 0 && arr[j] > temp; j -= gap) {arr[j + gap] = arr[j];}arr[j + gap] = temp;console.log('arr :', arr);}}console.timeEnd('希尔排序耗时');return arr;
};
测试
// 测试
const array = [35, 33, 42, 10, 14, 19, 27, 44];
console.log('原始array:', array);
const newArr = shellSort(array);
console.log('newArr:', newArr);
// 原始 array: [35, 33, 42, 10, 14, 19, 27, 44]
// arr : [14, 33, 42, 10, 35, 19, 27, 44]
// arr : [14, 19, 42, 10, 35, 33, 27, 44]
// arr : [14, 19, 27, 10, 35, 33, 42, 44]
// arr : [14, 19, 27, 10, 35, 33, 42, 44]
// arr : [14, 19, 27, 10, 35, 33, 42, 44]
// arr : [14, 19, 27, 10, 35, 33, 42, 44]
// arr : [10, 14, 19, 27, 35, 33, 42, 44]
// arr : [10, 14, 19, 27, 35, 33, 42, 44]
// arr : [10, 14, 19, 27, 33, 35, 42, 44]
// arr : [10, 14, 19, 27, 33, 35, 42, 44]
// arr : [10, 14, 19, 27, 33, 35, 42, 44]
// 希尔排序耗时: 3.592041015625ms
// newArr: [10, 14, 19, 27, 33, 35, 42, 44]
分析
第一,希尔排序是原地排序算法吗 ?
希尔排序过程中,只涉及相邻数据的交换操作,只需要常量级的临时空间,空间复杂度为 O(1) 。所以,希尔排序是原地排序算法。
第二,希尔排序是稳定的排序算法吗 ?
我们知道,单次直接插入排序是稳定的,它不会改变相同元素之间的相对顺序,但在多次不同的插入排序过程中,相同的元素可能在各自的插入排序中移动,可能导致相同元素相对顺序发生变化。
因此,希尔排序不稳定。
第三,希尔排序的时间复杂度是多少 ?
最佳情况:T(n) = O(n log n)。
最差情况:T(n) = O(n log2 n)。
平均情况:T(n) = O(n log2 n)。
动画
堆排序(Heap Sort)
堆的定义
堆其实是一种特殊的树。只要满足这两点,它就是一个堆。
堆是一个完全二叉树。
完全二叉树:除了最后一层,其他层的节点个数都是满的,最后一层的节点都靠左排列。
堆中每一个节点的值都必须大于等于(或小于等于)其子树中每个节点的值。
也可以说:堆中每个节点的值都大于等于(或者小于等于)其左右子节点的值。这两种表述是等价的。
对于每个节点的值都大于等于子树中每个节点值的堆,我们叫作大顶堆。
对于每个节点的值都小于等于子树中每个节点值的堆,我们叫作小顶堆。
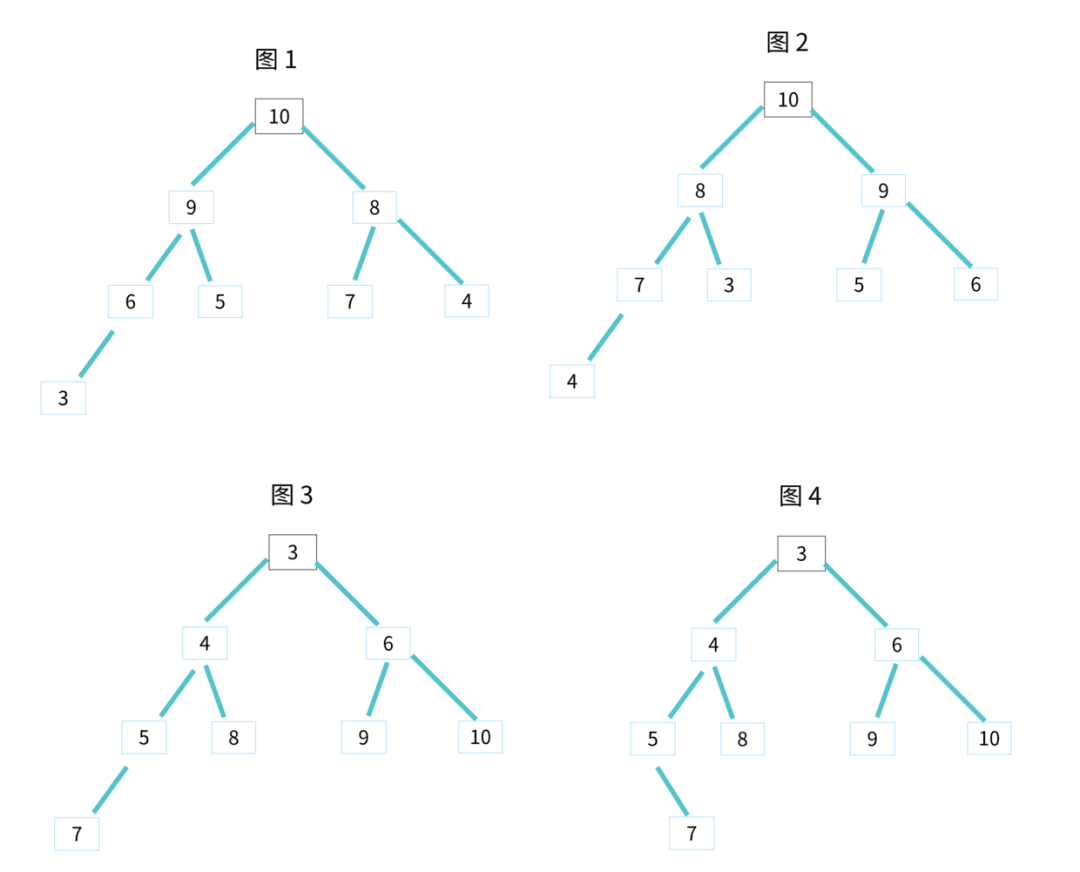
其中图 1 和 图 2 是大顶堆,图 3 是小顶堆,图 4 不是堆。除此之外,从图中还可以看出来,对于同一组数据,我们可以构建多种不同形态的堆。
思想
- 将初始待排序关键字序列 (R1, R2 … Rn) 构建成大顶堆,此堆为初始的无序区;
- 将堆顶元素 R[1] 与最后一个元素 R[n] 交换,此时得到新的无序区 (R1, R2, … Rn-1) 和新的有序区 (Rn) ,且满足 R[1, 2 … n-1] <= R[n]。
- 由于交换后新的堆顶 R[1] 可能违反堆的性质,因此需要对当前无序区 (R1, R2 … Rn-1) 调整为新堆,然后再次将 R[1] 与无序区最后一个元素交换,得到新的无序区 (R1, R2 … Rn-2) 和新的有序区 (Rn-1, Rn)。不断重复此过程,直到有序区的元素个数为 n - 1,则整个排序过程完成。
实现
// 堆排序
const heapSort = array => {console.time('堆排序耗时');// 初始化大顶堆,从第一个非叶子结点开始for (let i = Math.floor(array.length / 2 - 1); i >= 0; i--) {heapify(array, i, array.length);}// 排序,每一次 for 循环找出一个当前最大值,数组长度减一for (let i = Math.floor(array.length - 1); i > 0; i--) {// 根节点与最后一个节点交换swap(array, 0, i);// 从根节点开始调整,并且最后一个结点已经为当前最大值,不需要再参与比较,所以第三个参数为 i,即比较到最后一个结点前一个即可heapify(array, 0, i);}console.timeEnd('堆排序耗时');return array;
};
// 交换两个节点
const swap = (array, i, j) => {let temp = array[i];array[i] = array[j];array[j] = temp;
};
// 将 i 结点以下的堆整理为大顶堆,注意这一步实现的基础实际上是:
// 假设结点 i 以下的子堆已经是一个大顶堆,heapify 函数实现的
// 功能是实际上是:找到 结点 i 在包括结点 i 的堆中的正确位置。
// 后面将写一个 for 循环,从第一个非叶子结点开始,对每一个非叶子结点
// 都执行 heapify 操作,所以就满足了结点 i 以下的子堆已经是一大顶堆
const heapify = (array, i, length) => {let temp = array[i]; // 当前父节点// j < length 的目的是对结点 i 以下的结点全部做顺序调整for (let j = 2 * i + 1; j < length; j = 2 * j + 1) {temp = array[i]; // 将 array[i] 取出,整个过程相当于找到 array[i] 应处于的位置if (j + 1 < length && array[j] < array[j + 1]) {j++; // 找到两个孩子中较大的一个,再与父节点比较}if (temp < array[j]) {swap(array, i, j); // 如果父节点小于子节点:交换;否则跳出i = j; // 交换后,temp 的下标变为 j} else {break;}}
};
测试
const array = [4, 6, 8, 5, 9, 1, 2, 5, 3, 2];
console.log('原始array:', array);
const newArr = heapSort(array);
console.log('newArr:', newArr);
// 原始 array: [4, 6, 8, 5, 9, 1, 2, 5, 3, 2]
// 堆排序耗时: 0.15087890625ms
// newArr: [1, 2, 2, 3, 4, 5, 5, 6, 8, 9]
分析
第一,堆排序是原地排序算法吗 ?
整个堆排序的过程,都只需要极个别临时存储空间,所以堆排序是原地排序算法。
第二,堆排序是稳定的排序算法吗 ?
因为在排序的过程,存在将堆的最后一个节点跟堆顶节点互换的操作,所以就有可能改变值相同数据的原始相对顺序。
所以,堆排序是不稳定的排序算法。
第三,堆排序的时间复杂度是多少 ?
堆排序包括建堆和排序两个操作,建堆过程的时间复杂度是 O(n),排序过程的时间复杂度是 O(nlogn),所以,堆排序整体的时间复杂度是 O(nlogn)。
最佳情况:T(n) = O(nlogn)。
最差情况:T(n) = O(nlogn)。
平均情况:T(n) = O(nlogn)。
动画

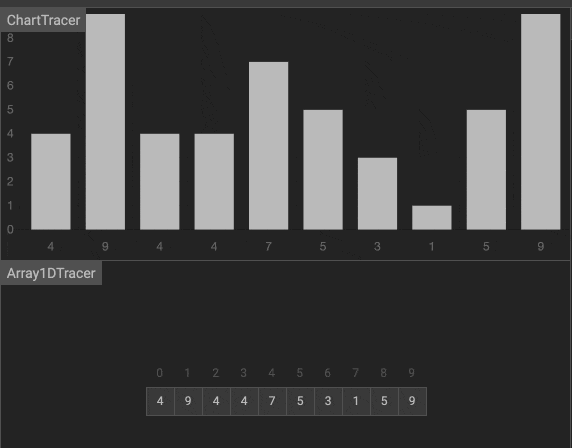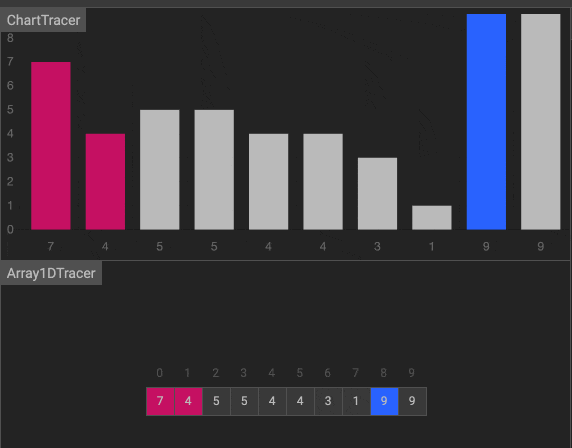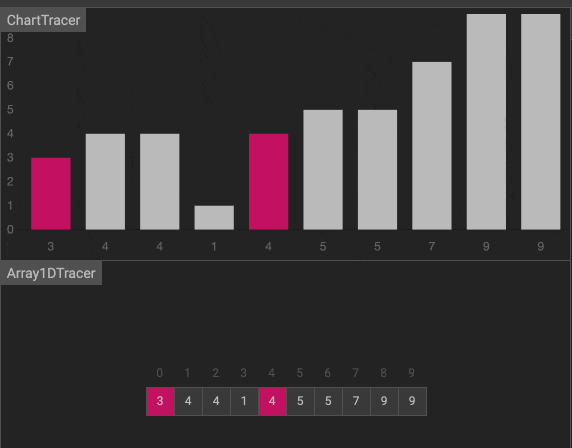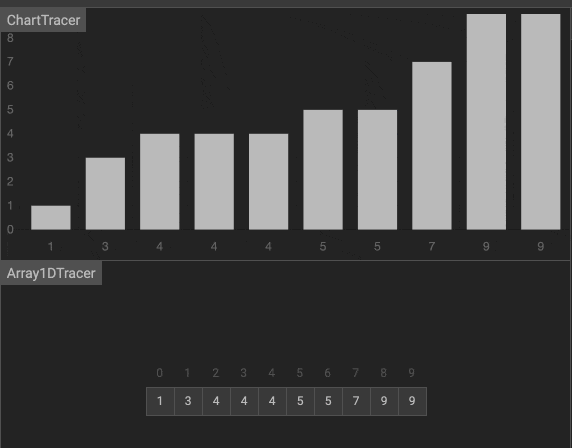
排序算法的复杂性对比
复杂性对比
| 名称 | 平均 | 最好 | 最坏 | 空间 | 稳定性 | 排序方式 |
|---|---|---|---|---|---|---|
| 归并排序 | O(n log n) | O(n log n) | O(n log n) | O(n) | Yes | Out-place |
| 快速排序 | O(n log n) | O(n log n) | O(n2) | O(logn) | No | In-place |
| 希尔排序 | O(n log n) | O(n log2 n) | O(n log2 n) | O(1) | No | In-place |
| 堆排序 | O(n log n) | O(n log n) | O(n log n) | O(1) | No | In-place |
算法可视化工具
算法可视化工具 algorithm-visualizer
算法可视化工具 algorithm-visualizer 是一个交互式的在线平台,可以从代码中可视化算法,还可以看到代码执行的过程。
效果如下图。
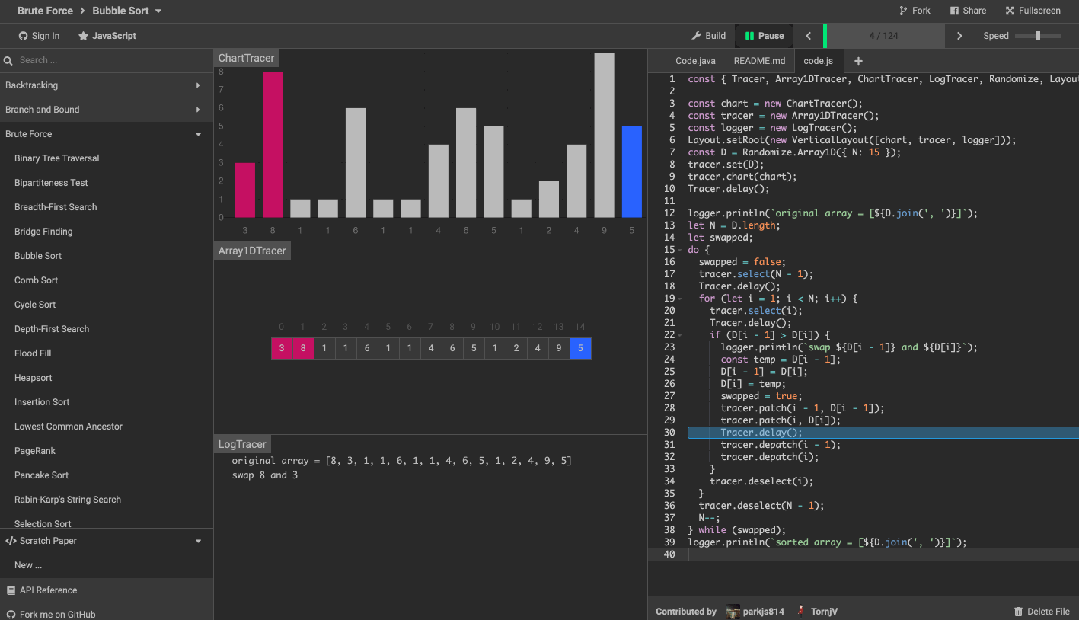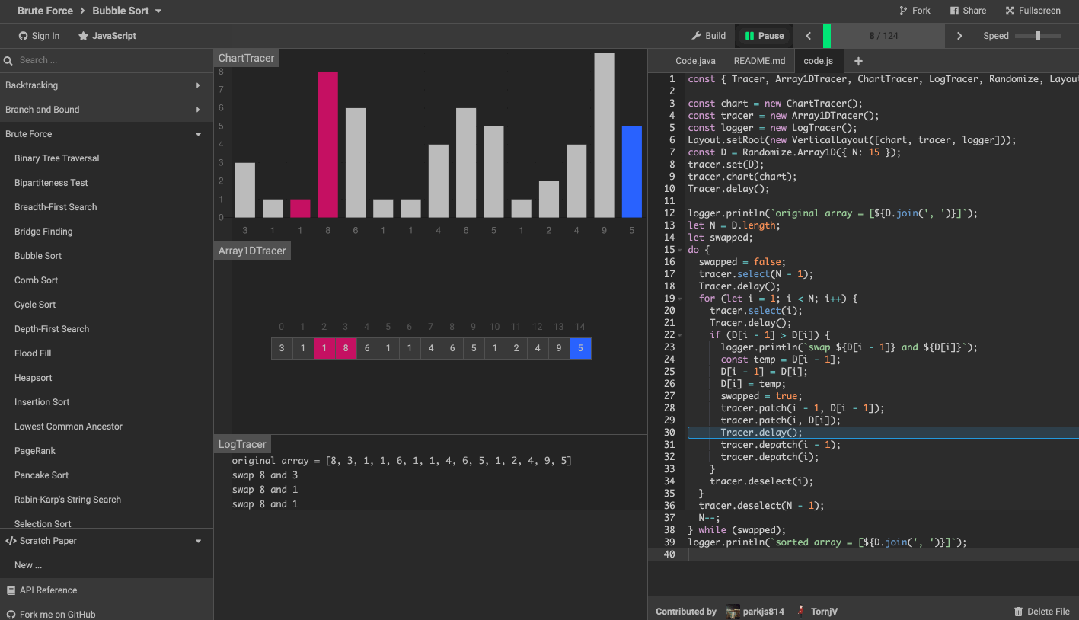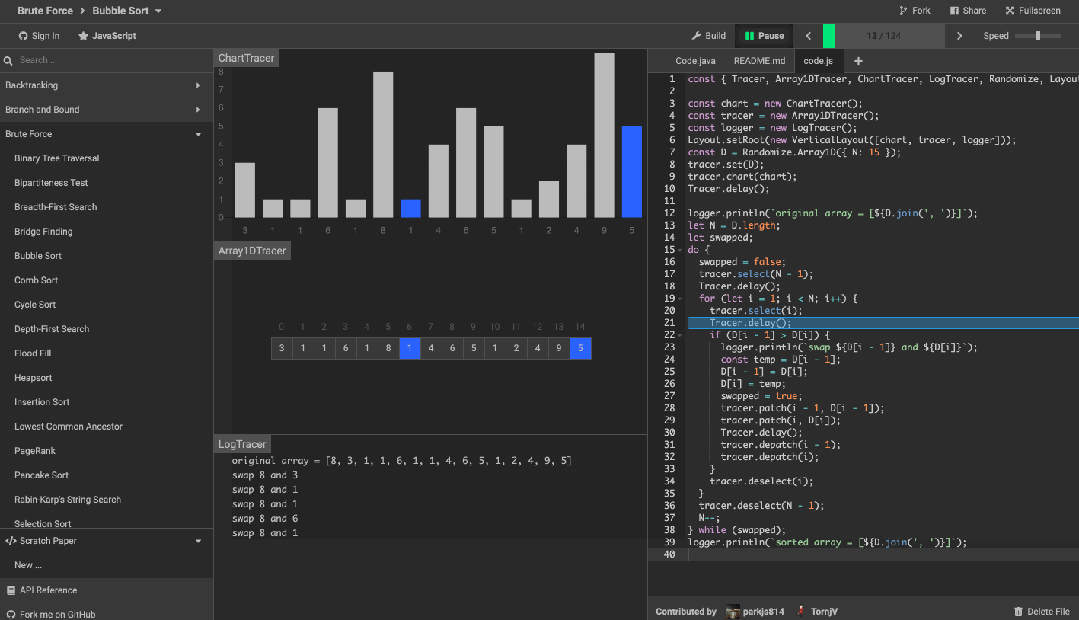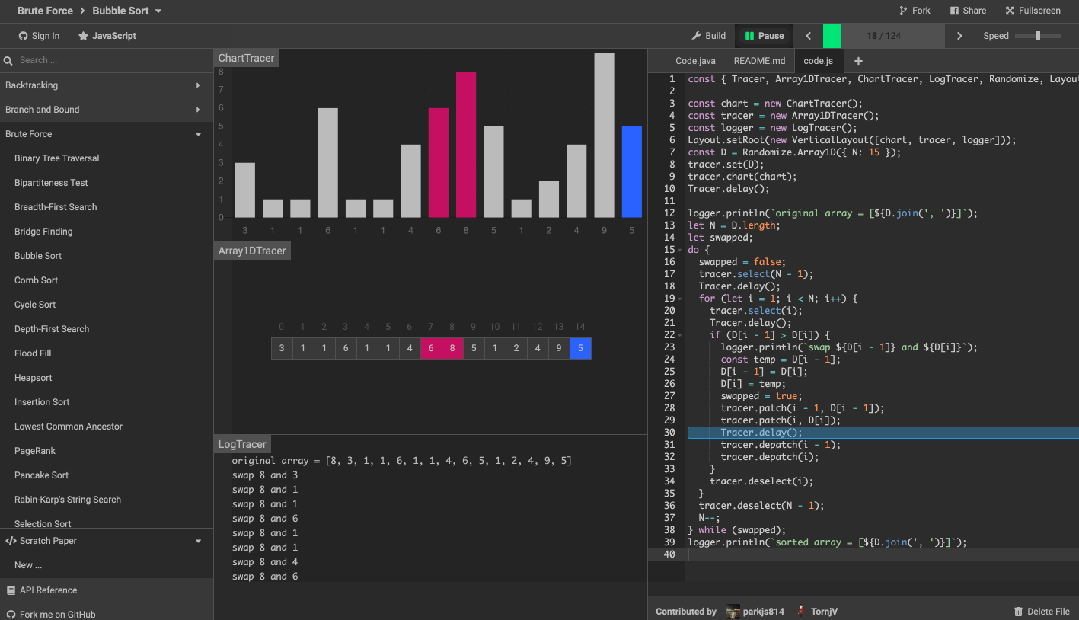
旨在通过交互式可视化的执行来揭示算法背后的机制。
算法可视化来源 https://visualgo.net/en
效果如下图。

https://www.ee.ryerson.ca
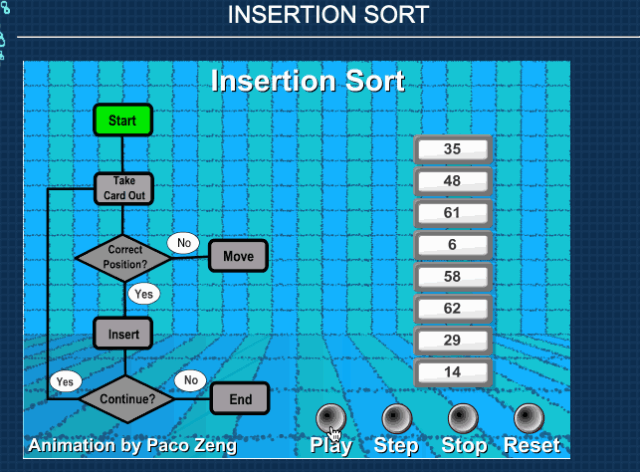
illustrated-algorithms
变量和操作的可视化表示增强了控制流和实际源代码。您可以快速前进和后退执行,以密切观察算法的工作方式。

参考文档
- https://www.shuzhiduo.com/A/1O5E3BPWz7/






 #学习方法#经验分享)

】StateBackend的整体设计、StateBackend创建说明)
2022国赛真题:水果消消乐)
)


原理及Python实现)





