前言
Microsoft Office是由Microsoft(微软)公司开发的一套基于 Windows 操作系统的办公软件套装。常用组件有 Word、Excel、PowerPoint、Access、Outlook等。
准备工作
1、Win7 及以上系统
2、提前准备好 Office 2013 安装包
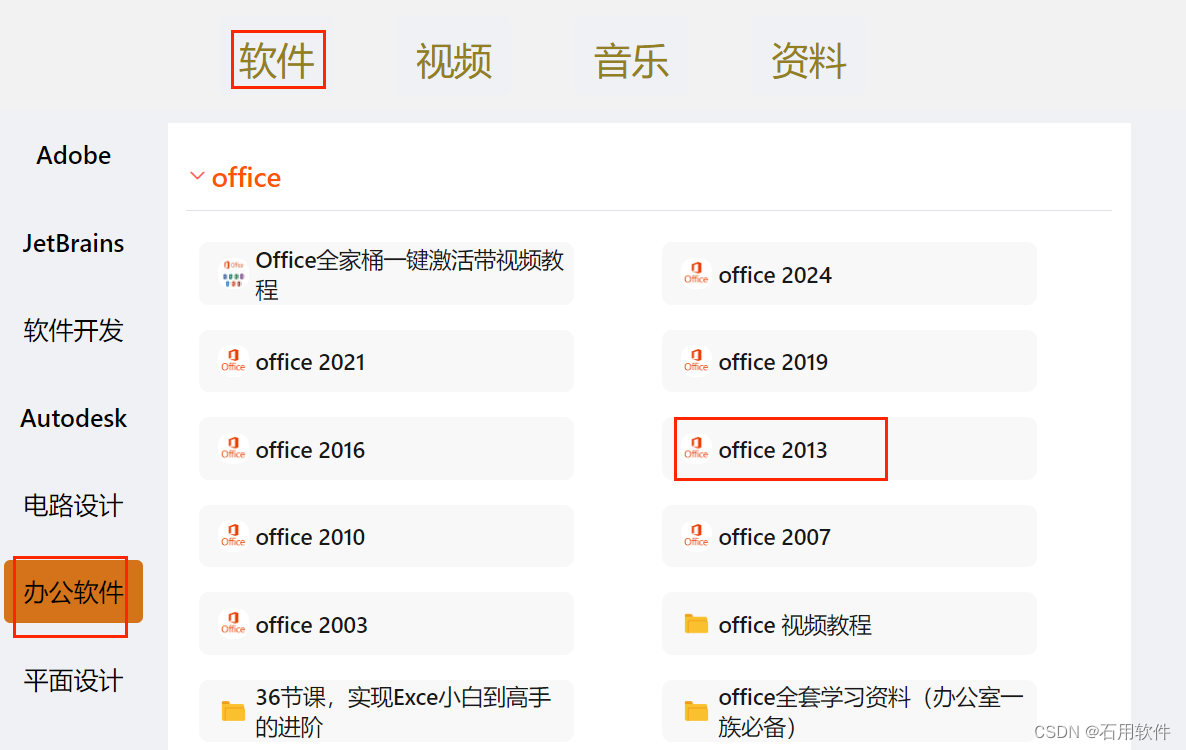
安装步骤
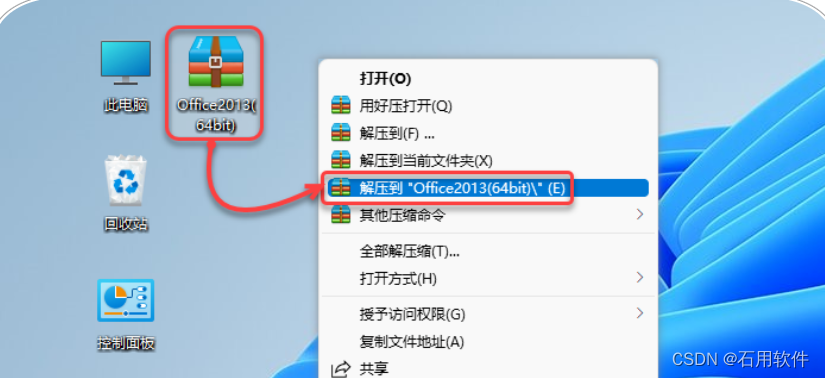
1.鼠标右击【Office2013(64bit)】压缩包选择（win11系统需先点击“显示更多选项”）【解压到 Office2013(64bit)】。
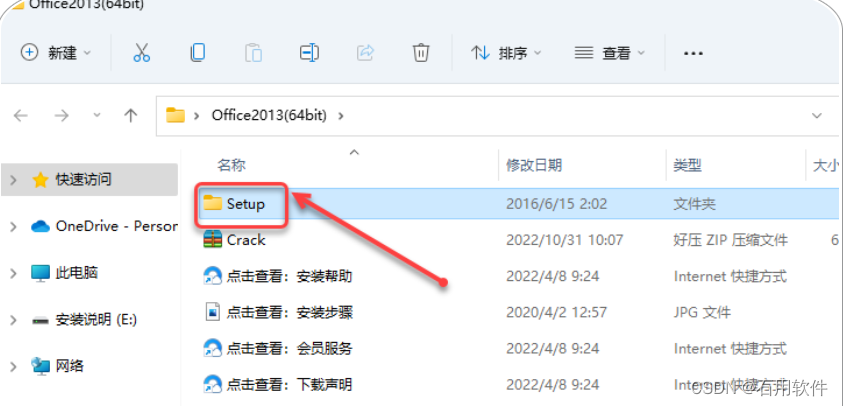
2.打开解压后的文件夹，双击打开【Setup】文件夹。
3.鼠标右击【Setup】选择【以管理员身份运行】。
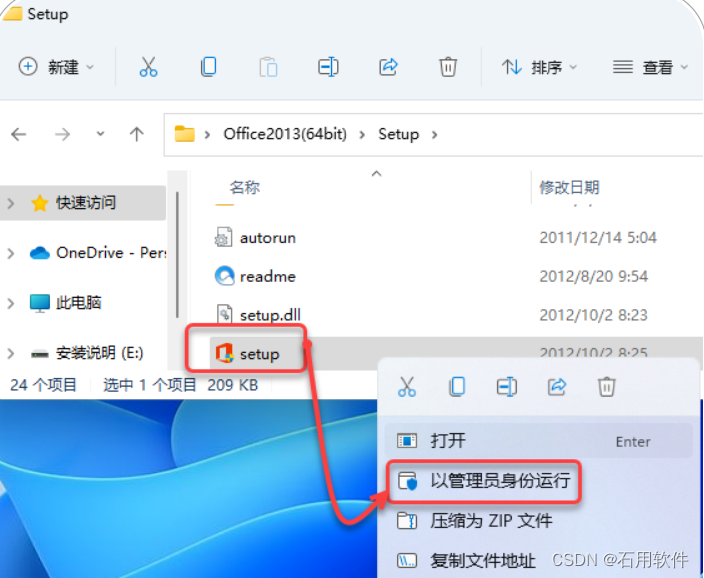
4.勾选【我接受此协议的条款】，点击【继续】。
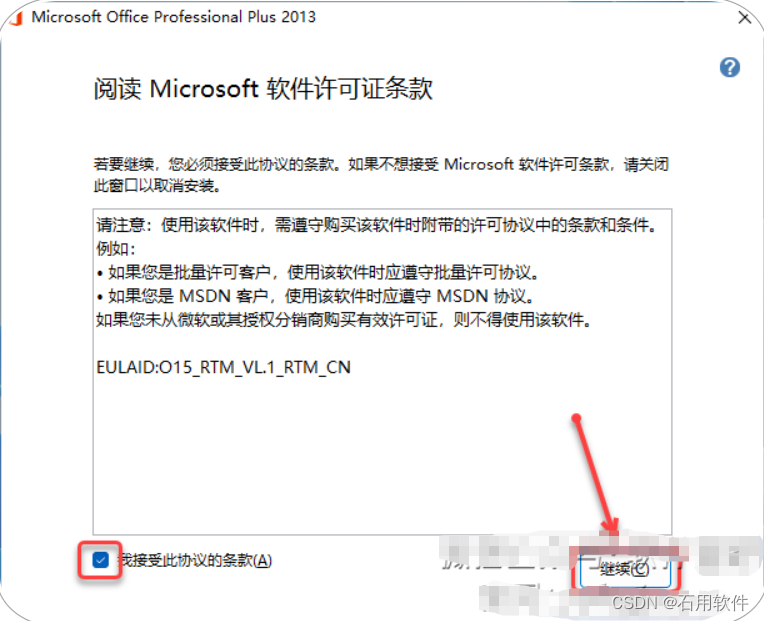
5.点击【自定义】。
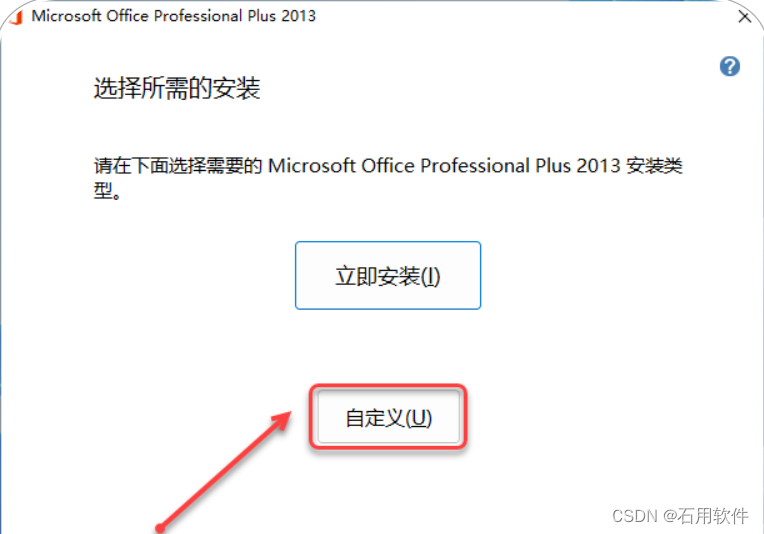
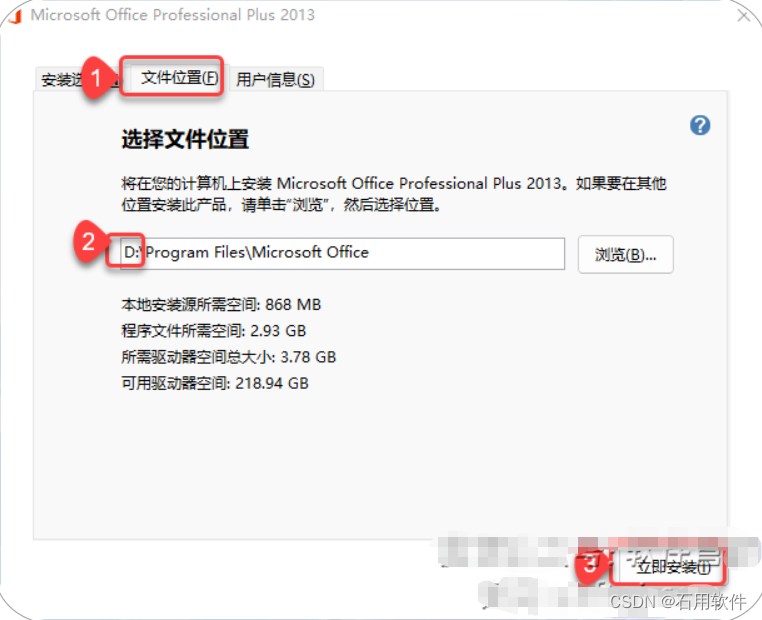
6.①点击【文件位置】
②修改路径地址中的首字符C可修改安装位置（如：将C改为D表示安装到D盘）
③点击【立即安装】。
7.安装中……
8.点击【关闭】。
9.打开安装包解压后的【Office2013(64bit)】文件夹，鼠标右击【Crack】选择【解压到当前文件夹】。
解压【Crack】前：先关闭“所有杀毒软件(部分电脑自带的“迈克菲”也要关闭）、防火墙、Windows Defender”，否则可能会被杀毒软件误杀无法运行。
10.鼠标右击解压出来的【Crack】选择【以管理员身份运行】。
11.点击【开始】。
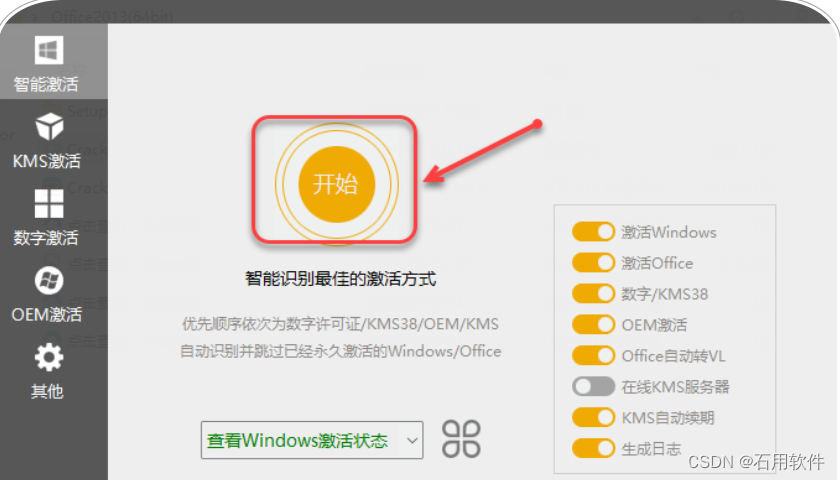
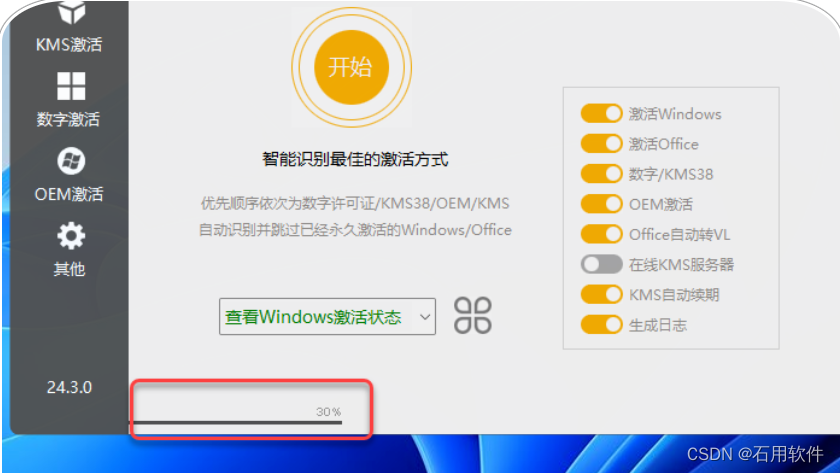
12.激活中……
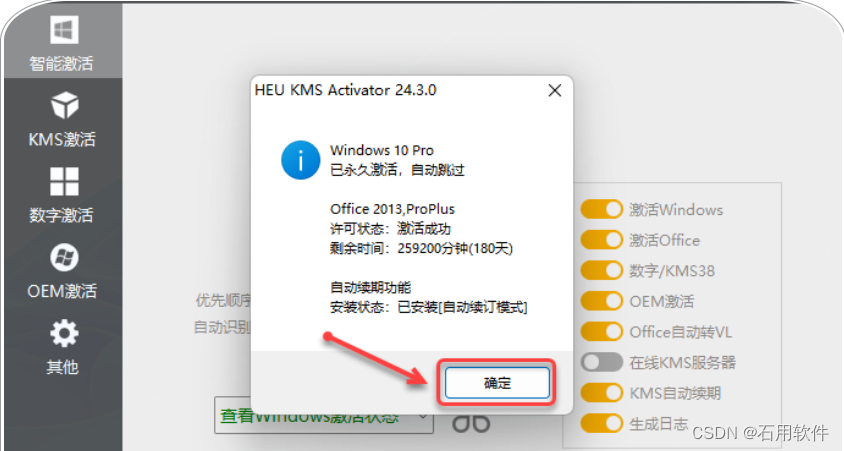
13.点击【确定】。
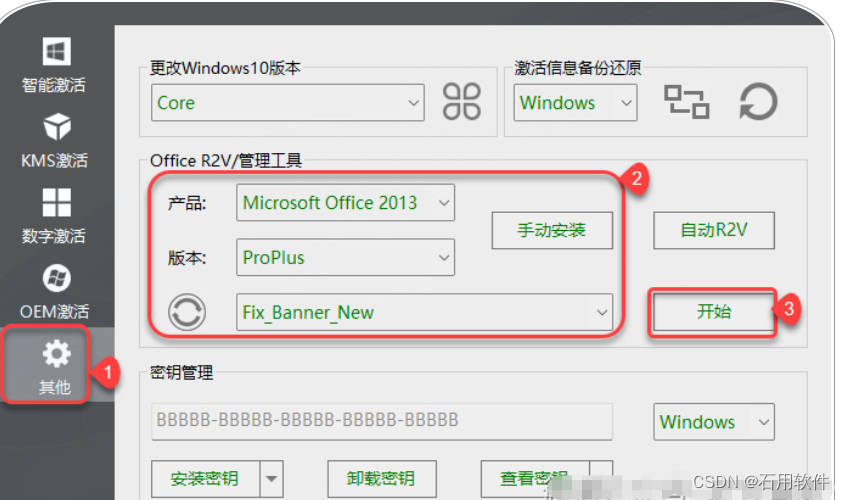
14.①点击【其它】
②选择产品【Microsoft Office 2013】；选择版本选择【ProPlus】；选择类型【Fix_Banner_New】
③点击【开始】。
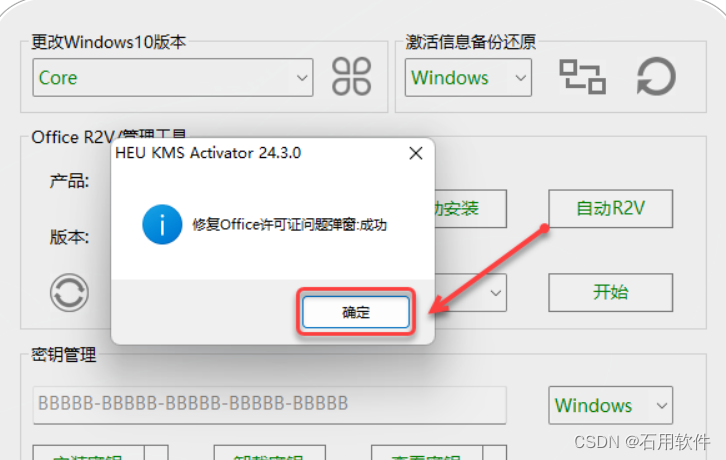
15.点击【确定】。
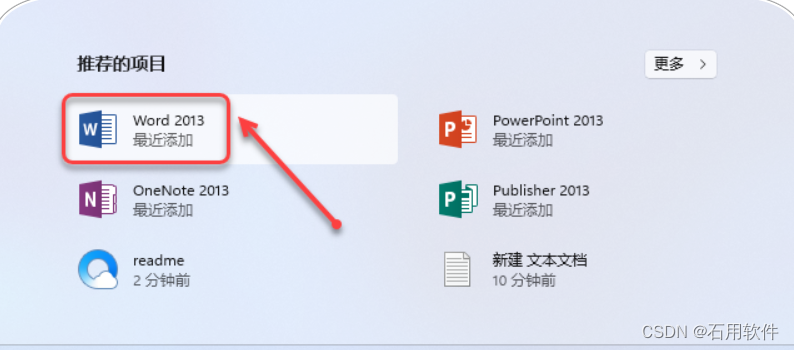
16.点击桌面任务栏中的【开始图标】，点击需要启动的office产品图标启动软件（如：word2013）；在开始菜单“所有应用”中可启动其它产品（如：ppt、excel）。
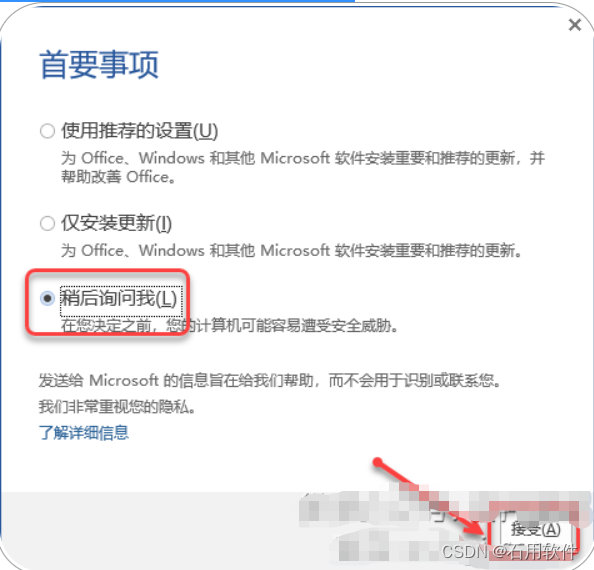
17.选择【稍后询问我】，点击【接受】。
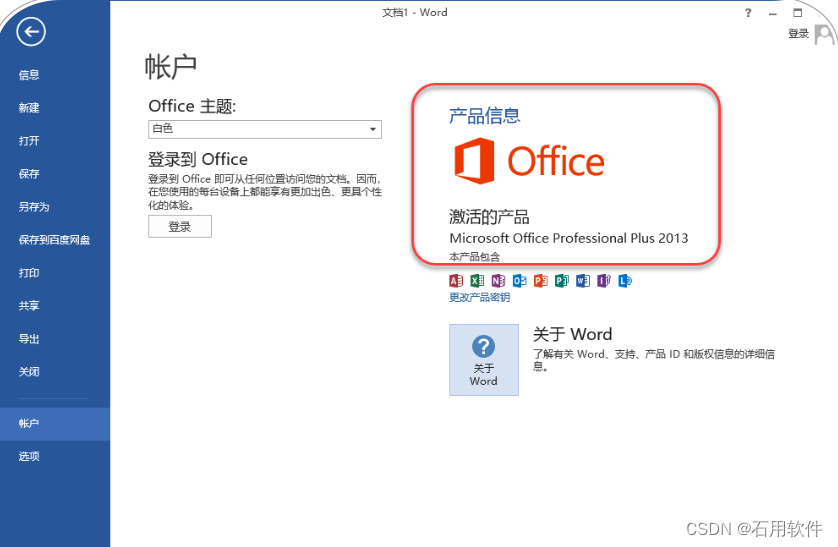
18.安装成功！
