目录
一、前言
二、正文
Ⅰ.主成分分析
Ⅱ.核主成分分析
三、结语
一、前言
前面介绍的特征选择方法获得的特征,是从原始数据中抽取出来的,并没有对数据进行变换。而特征提取和降维,则是对原始数据的特征进行相应的数据变换,并且通常会选择比原始特征数量少的特征,同时达到数据降维的目的。常用的数据特征提取和降维的方法有主成分分析,核成分分析,流行学习,t-SNE,多维尺度分析等方法。
二、正文
from sklearn.decomposition import PCA,KernelPCA
from sklearn.manifold import Isomap,MDS,TSNE
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import load_wine
wine_x,wine_y=load_wine(return_X_y=True)
wine_x=StandardScaler().fit_transform(wine_x)
在介绍特征提取和降维的方法之前,我们先导包读取相应的数据。 通过标准化进行数据特征变换的处理。
Ⅰ.主成分分析
pca=PCA(n_components=13,random_state=123)
pca.fit(wine_x)
exvar=pca.explained_variance_
plt.figure(figsize=(10,6))
plt.plot(exvar,'r-o')
plt.hlines(y=1,xmin=0,xmax=12)
plt.xlabel('number')
plt.ylabel('PCA')
plt.show()
主成分分析法(Principal Component Analysis,PCA)是采用一种数学降维的方法,在损失很少信息的前提下,找出几个综合变量为主成分,来代替原来众多的变量,使这些主成分尽可能地代表原始数据的信息,其中每个主成分都是原始变量的线性组合,而且各个主成分之间不相关(即线性无关)。通过主成分分析,我们可以从事物错综复杂的关系中找到一些主要成分(通常选择累积 贡献率≥85%的前m个主成分),从而能够有效利用大量统计信息进行定性分析,揭示变量之间的内在关系,得要一些事物特征及其发展规律的深层次信息和启发,推动研究进一步深入。通常使用主成分个数远小于原始特征个数,使用起到特征提取和降维的目的。
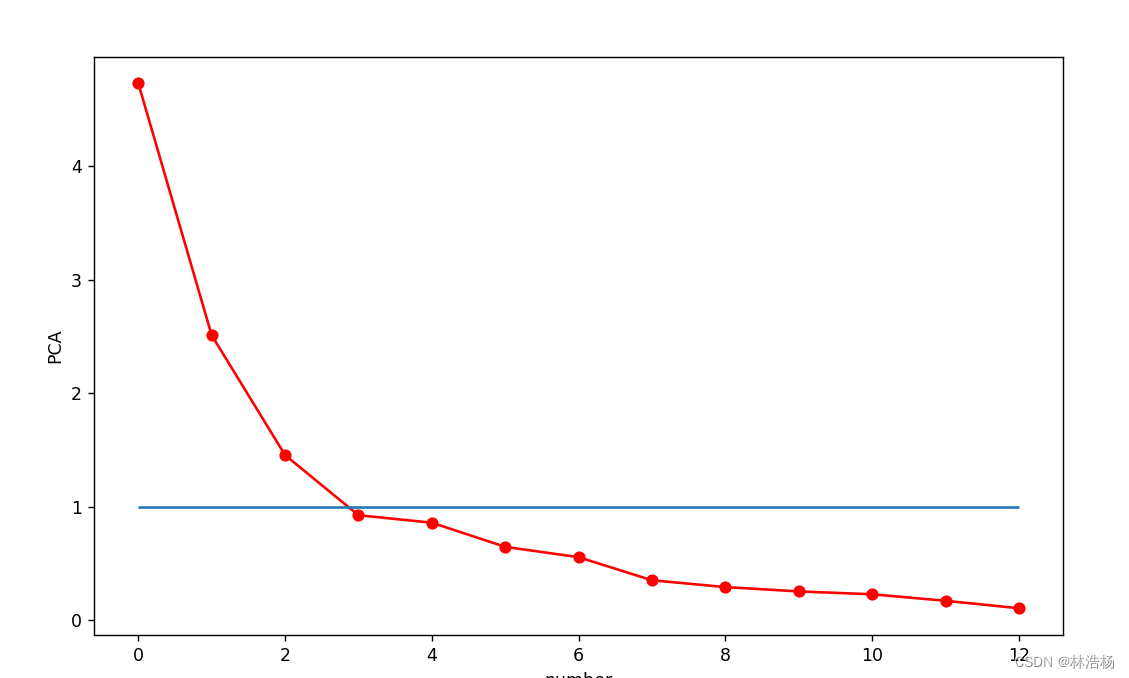
从结果分析,使用数据的前三个主成分即可对其进行良好的数据建模。
pca_wine_x=pca.transform(wine_x)[:,0:3]
print(pca_wine_x.shape)
#输出结果
(178,3)
如上我们可以知道,前三个主成分可对其数据建模,于是我们pca进行数据变换之后对其进行切片,前三列的数据。
colors=['red','blue','green']
shape=['o','s','*']
fig=plt.figure(figsize=(10,6))
ax1=fig.add_subplot(111,projection='3d')
for ii,y in enumerate(wine_y):ax1.scatter(pca_wine_x[ii,0],pca_wine_x[ii,1],pca_wine_x[ii,2],s=40,c=colors[y],marker=shape[y])ax1.set_xlabel('pca1',rotation=20)
ax1.set_ylabel('pca2',rotation=20)
ax1.set_zlabel('pca3',rotation=20)
ax1.azim=225
ax1.set_title('pca')
plt.show()
先将三种成分分别的颜色和标记封装在列表当中,然后设置窗口, 111是设置位置即第一行第一列的第一个格子,则会也就意味着这里只有一个图,projection(映射)参数设置为3d,然后将前三个主成分通过循环在三维空间画出其数据分布。
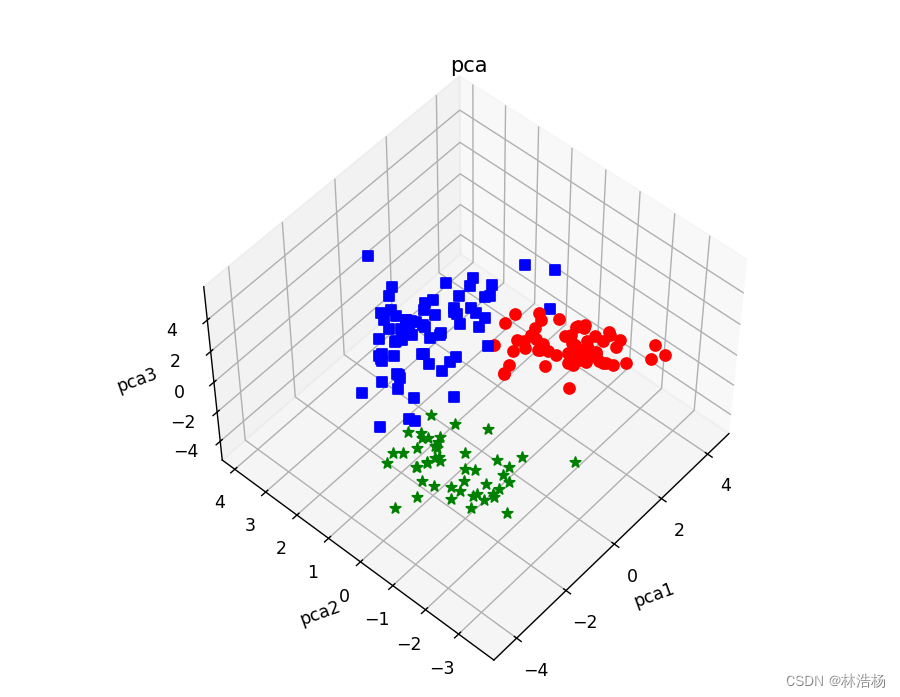
这样我们就能区分出三个主成分的数据分布情况,即不同类别的分布情况。
Ⅱ.核主成分分析
PCA是线性的数据降维技术,而核主成分分析则是针对非线性的数据表示,对其进行特征提取并数据降维。
kpca=KernelPCA(n_components=13,kernel='rbf',gamma=0.2,random_state=123)
kpca.fit(wine_x)
eigenvalues=kpca.eigenvalues_
plt.figure(figsize=(10,6))
plt.plot(eigenvalues,'r-o')
plt.hlines(y=4,xmin=0,xmax=12)
plt.xlabel('number')
plt.ylabel('KernelPCA')
plt.show()
方法与主成分分析大差不大,但是这里注意一个KernelPCA类中的一个属性:
eigenvalues_:Eigenvalues of the centered kernel matrix in decreasing order. If
n_componentsandremove_zero_eigare not set, then all values are stored.
翻译过来就是:中心核向量的特征值按照降序排序,如果未设置n_components和remove_zero_eig,则存储所有值。
原本这个属性叫做lambdas_,但是被更改为eigenvalues_(特征值)。

同样针对前三个核主成分,可以在三维空间将数据分布进行可视化。
kpca_wine_x=kpca.transform(wine_x)[:,0:3]
print(kpca_wine_x.shape)
colors=['red','blue','green']
shape=['o','s','*']
fig=plt.figure(figsize=(10,6))
ax1=fig.add_subplot(111,projection='3d')
for ii,y in enumerate(wine_y):ax1.scatter(kpca_wine_x[ii,0],kpca_wine_x[ii,1],kpca_wine_x[ii,2],s=40,c=colors[y],marker=shape[y])ax1.set_xlabel('kpca1',rotation=20)
ax1.set_ylabel('kpca2',rotation=20)
ax1.set_zlabel('kpca3',rotation=20)
ax1.azim=225
ax1.set_title('kpca')
plt.show()
做法跟主成分大差不差,利用散点在空间中的分布来发现其中的数据分布情况。
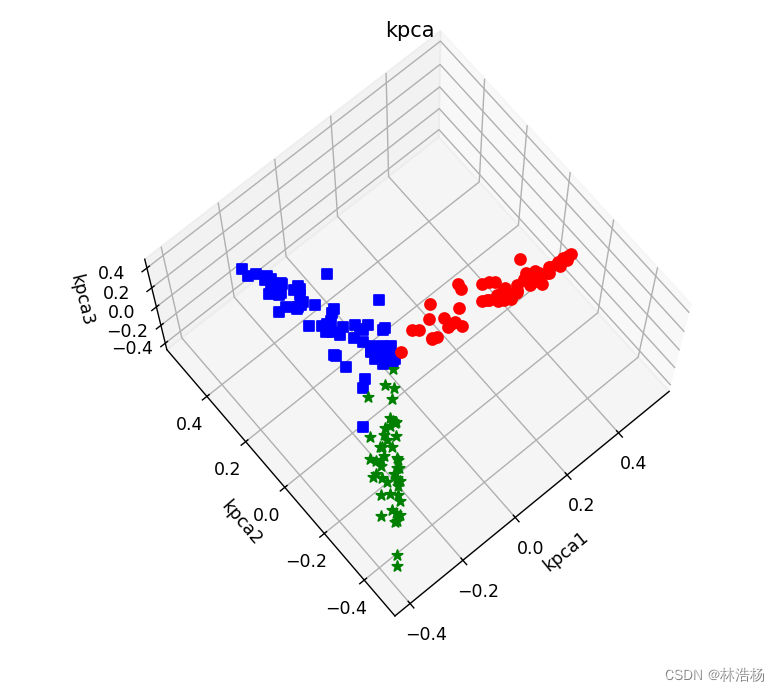
可以看出核主成分分析与主成分分析之间的主成分核成分之间的数据分布情况大有不同。
三、结语
上篇我们先从线性与非线性入手,希望能对你提供帮助,点赞收藏以备不时之需,关注我,有关新的数据分析的文章第一时间告知于你













Hot-Plug机制)

媒体中心解决方案。)



