1.机器人姿态的其他表示方法

    前面说的用3×3矩阵矩阵描述姿态，9个元素，6个约束条件，实际上只有3个独立元素。即用3个独立元素即可描述机器人姿态。常用的有RPY角，欧拉角和四元数。

1.1  RPY角

RPY角是船舶在海上航行时常用的一种姿态表示方法，其笛卡尔坐标建立方法如下：以船头前进方向为Z轴，以垂直于甲板平面的法线向上方向为X轴，Y轴依据右手法则由X、Z确定。定义绕Z轴的转动为Roll(翻滚)，转角为；绕Y轴的转动为Pitch(俯仰)，转角为，绕X轴的转动为Yaw(偏航)，转角为。可以看出来RPY的名称来源于Roll、Pitch、Yaw三个单词的首字母。

实质是一个绕固定坐标系的多个坐标轴旋转的问题。

有意思的是逆解问题：即从一个旋转矩阵等价推出X-Y-Z固定角坐标系。逆解取决于求解一组超越方程：已知一个旋转矩阵，则有9个方程和3个未知量。

1.2  欧拉角

欧拉角是瑞士数学家Leonhard Euler提出的采用绕运动坐标系的三个坐标轴的转角组合描述刚体姿态的方法，与RPY角类似，也是采用了三个角度变量。该方法广泛用于数学，物理学，航空工程及刚体动力学。

欧拉角有多种类型，绕不小于两个坐标轴的三个转角的组合都可以表示成欧拉角。第一次转动可以绕三个笛卡尔坐标轴中的任何一个,第二次转动可以绕其余两轴之一进行,第三次转动方向只要不同于第二次就可以,所以也存在两种选择．这样欧拉角总共有3×2×2＝12种定义方式.

实质是一个绕动坐标系的多个坐标轴旋转的问题。

1.3  四元数

一般来说用欧拉角表示刚体的姿态或运动都是简单有效的，但是在某些特殊的情况下，欧拉角会出现所谓的万向节死锁问题，即欧拉角无法描述刚体的运动。出现万向节死锁问题的原因是采用有序的三个角度的欧拉角方法并不能描述所有的刚体运动。

1.3.1 四元数的定义及特点

1843年爱尔兰数学家William Rowan Hamilton在研究将复数从描述二维空间扩展到高维空间时，创造出了一个超复数：四元数(Quaternion)。四元数能表示四维空间，由一个实数单位1和三个虚数单位i、j、k组成，通常表示形式为：

q = a + bi + cj + dk

式中，a、b、c、d均为实数，i、j、k被称为第一、第二、第三维虚单位，具有下列性质：

i2 = j2 = k2 = -1

ij = -ji = k; jk = -kj = i; ki = -ik = j

为了表达简便，通常将四元数写成一个实数和一个向量组合的形式：

q = (a, v) = (a, b, c, d)

上式中，v是一个向量,v = bi + cj + dk, a、b、c、d为4个有序的实数。四元数可以看作是一种实数和向量表达的一般形式，实数可看作是虚部为0的四元数，而向量可看作为实部为0的四元数，也被称为纯四元数。任意的三维向量都可以转化为纯四元数。

四元数具有下列特点：

①可避免万向节死锁

②几何意义明确，只需4个数就可以表示绕过原点任意向量的旋转

③计算效率高

④比欧拉角多了一个维度，理解困难

2.一般坐标系的映射与齐次矩阵

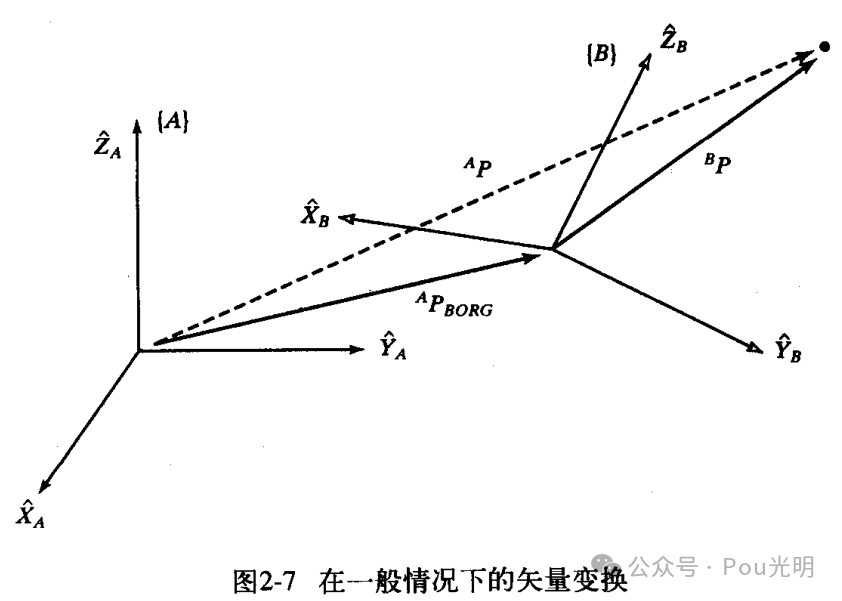
经常有这种情况：已知矢量相对坐标系{B}的描述，想求出它对另一个坐标系{A}的描述。考虑一般情况，{B}与{A}原点不重合，有一个偏移矢量。{B}的原点矢量用PB表示，{B}相对于{A}用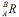描述(B相对于A)。已知PB求PA。

首先将PB变换到一个中间坐标系，该坐标系与{A}姿态相同，原点与{B}重合。 则：

PA = 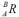PB +  

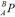
该式表示将一个矢量描述从一个坐标系变换到另一个坐标系的一般变换映射。由上式可以得到另一新的概念形式：

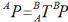
即用一个矩阵形式的算子表示从一个坐标系到另一个坐标系的映射。

 

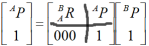
换言之：

①在4×1矢量中增加的最后一个分量为“1”

②在4×4矩阵中增加的最后一行分量为“[0 0 0 1]”

我们知道笛卡尔坐标系中位置可以用3×1或4×1矢量表示，取决于它与3×3还是4×4矩阵相乘。上面的4×4矩阵称为齐次矩阵。在其他领域，可被用于投影和比例运算。它可以看做用一个简单的矩阵形式表示了一般的旋转和平移，即一种线性变换，该变换(常用齐次变换)可以定义一个坐标系。

往期系列回顾：

机械臂运动学正解验证

Matlab机械臂运动学示教演示

机械臂运动学D-H参数学习笔记(2)

3_机械臂运动学之刚体的运动

4_机械臂运动学基础向量空间

5_机械臂运动学基础_矩阵

6_机械臂运动学_刚体转动的描述

7机器人位姿的数学描述与坐标变

9_机械臂运动学_正解C++推导验证

10_机械臂运动学_机械臂C++逆解——2023

欢迎关注，了解更多学习笔记！