目录
1 空间相关的群,环,域,集合,空间的预备知识
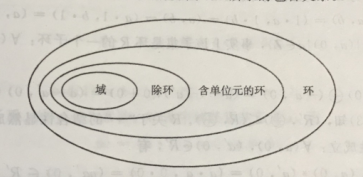
1.1:群,环,域,集合,空间的定义(表示不懂,只是做个标记)
2 空间
2.1 各种空间概念
3 标量空间
4 向量空间/张成空间/线性空间(vector space/ linear space)
4.1 线性空间定义
4.2 向量空间的表现
4.3 加法和数乘的封闭性
4.4 先有“线性组合” 这个概念
4.5 线性组合的意思
4.5.1 线性组合的具体方法
4.6 线性变换
4.7 线性变换(线性映射)的意义?
5 仿射空间(affine space)
5.1 内容
5.2 仿射空间和线性空间的区别
6 欧几里得空间(Euclidean space)
7 向量的各种距离
7.1 曼哈顿距离
7.2 欧氏距离
7.3 切比雪夫距离
7.4 向量的长度和角度
1 空间相关的群,环,域,集合,空间的预备知识
1.1:群,环,域,集合,空间的定义(表示不懂,只是做个标记)
- 这部分内容是摘抄
- 集:集合可以理解为一些对象的无序的集合体
- 群:群是一种具有特定运算和性质的集合,群是在集合的基础上引入了一个二元运算(如加法或乘法),并满足封闭性、结合律、单位元和逆元这四个性质,可以理解为任意两个元素的和还在群内,就叫作群。群只有一种加法运算?
- 环:最早指的是整数环,后来环又被称为代数,成为了代数学的标准对象。环是在群的基础上加入了另一种运算,并满足一定性质。因此,环是对群概念的扩展和加强。环是一种代数结构,包含两个运算,通常为加法和乘法。环需要满足加法构成群、乘法满足封闭性、结合律、分配律。
- 域:域是一个非常抽象的概念,域暗示了一种足够大的概念,在代数学里它能够作加减乘除运算,在数理逻辑里把函数有定义的集合称作定义域,取值的范围称作值域,在模型论里把所有数学对象构成的集合称作论域。域曾经被称为体。域在环的基础上要求乘法(除去乘法单位元外的元素)也构成一个交换群,即乘法需要满足交换律、单位元和逆元的性质。简言之,域是满足更严格性质的环。因此,域是对环概念的扩展和加强。
- 空间:可见空间跟这些深奥概念也是有关系的
数学中的群、域、环三者的严格数学定义是什么? - 知乎在集合 上定义一个二元运算 ,把它称为加法 。现在有一下这些法则:1)结合律:对于任意 有 2)存在…https://www.zhihu.com/question/449089514/answer/1777658855![]() https://www.zhihu.com/question/449089514/answer/1777658855数学【1】关于群、环、域、模 - 知乎读起来可能会有一点点乱,也可能会有一些语法上的奇怪,不要在意……引入-自然数集合先来说说自然数,不引用它的精确定义,先快速解释一波:“所有大于0的整数被称为自然数。(这里0不认为是自然数)” 那么将所有…https://zhuanlan.zhihu.com/p/336562401?utm_id=0
https://www.zhihu.com/question/449089514/answer/1777658855数学【1】关于群、环、域、模 - 知乎读起来可能会有一点点乱,也可能会有一些语法上的奇怪,不要在意……引入-自然数集合先来说说自然数,不引用它的精确定义,先快速解释一波:“所有大于0的整数被称为自然数。(这里0不认为是自然数)” 那么将所有…https://zhuanlan.zhihu.com/p/336562401?utm_id=0![]() https://zhuanlan.zhihu.com/p/336562401?utm_id=0
https://zhuanlan.zhihu.com/p/336562401?utm_id=0

2 空间
2.1 各种空间概念
- 一、距离空间(度量空间)
- 二、线性空间(向量空间)
- 三、范数空间(赋范空间)
- 四、线性赋范空间、线性度量空间
- 五、内积空间
- 六、巴拿赫空间和希尔伯特空间
- 赋范空间+完备性=巴拿赫空间
- 内积空间(无限维)+完备性=希尔伯特空间
- 七、拓扑空间
- 举例,如果距离是水果,范数是热带水果,那么拓扑就是植物。
以上空间分类参考下面文章
深刻理解空间(线性空间,度量空间,赋范空间,线性赋范空间,内积空间,巴拿赫空间以及希尔伯特空间)_非线性空间_CQ_Liu的博客-CSDN博客在我们学习矩阵理论和统计理论的时候,总是会出现“**空间”。在之前的时候对于空间理解的过程中,总是试图拿出一个具体的例子来加深自己的理解。但是这样做是不对的,因为如果说对于类似“欧几里何空间”这样的空间,跟我们生活中的三维空间极为相似,我们确实可以想象到一个具体的例子,但是对于类似“希尔伯特空间”之类的,我们很难用一个具体的实例来印证。所以,“**空间”到底是个什么东西呢?很感谢交大王老师的公..._非线性空间
https://blog.csdn.net/qq_34099953/article/details/84190508
在我们学习矩阵理论和统计理论的时候,总是会出现“**空间”。在之前的时候对于空间理解的过程中,总是试图拿出一个具体的例子来加深自己的理解。但是这样做是不对的,因为如果说对于类似“欧几里何空间”这样的空间,跟我们生活中的三维空间极为相似,我们确实可以想象到一个具体的例子,但是对于类似“希尔伯特空间”之类的,我们很难用一个具体的实例来印证。所以,“**空间”到底是个什么东西呢?
很感谢交大王老师的公开课“数学之旅”,通俗地解释了空间到底是个什么东西。附上链接:《数学之旅》——王维克。
下面我们从简单的距离空间开始,先理解空间是什么。
一、距离空间(度量空间)
从初中就开始学习“距离”的概念,我们总是想到这样一个情景:在三维坐标(空间)中有两个点(),则距离:
(1)
而距离所组成的空间是什么?我们能够用上式来理解距离空间吗?答案是最好不要。因为距离不只有形如上式(1)的直线距离,还有航海时的球面距离,还有路径中的折线距离等等。如下图:实际中我们从A到B的距离是折线距离。
对于距离,我们分别可以这样定义:
折线距离
最大距离
折线距离示例
既然是这样,我们应该如何去理解“距离空间”这个概念呢?为了便于理解,我们来举另外一个例子:字典中对苹果、水果的解释:苹果 双子叶植物,蔷薇科。落叶乔木。花淡红或淡紫红色。大多自花不孕,需异花授粉。果实由子房和花托发育而成。果肉清脆香甜,能帮助消化。
水果 供食用的含水分较多的植物果实的统称。为家庭或待客常用的果品。如梨﹑桃﹑苹果等。
热带水果
换句话说,苹果是一个具体的东西,因此我们可以用具体的表述来描述;而水果是一个抽象的集合,因此我们描述空间的时候,只能用其通用的属性。类比起来,苹果就好像是我们说的直线距离,而距离空间就是水果。这是一个抽象的东西,因此我们用这个集合中的元素所共有的属性来定义。空间中的元素,通俗来说交空间中的点。
所以我们可以这样来定义距离空间:
设X是非空集合,对于X中任意的两个元素x与y,按某一法则都对应唯一的实数d(x,y),而且满足下述三条公理:
(1)(非负性)d(x,y)≥0,[d(x,y)=0,当且仅当x=y];
(2)(对称性)d(x,y)=d(y,x);
(3)(三角不等式)对于任意的x,y,z∈X,恒有d(x,y)≤d(x,z)+d(z,y)。
则称d(x,y)为x与y的距离,并称X是以d为距离的距离空间。
二、线性空间(向量空间)
线性空间即定义了数乘和加法的空间,就是具有线性结构的空间。 有了线性空间的概念之后,因为有数乘和加法,所以空间中可以找到一组基底(Basis)能够通过线性组合得到空间中所有的点。并且满足八项规则(交换律、结合律等)。
三、范数空间(赋范空间)
设是的范数,满足:
(1)(非负性)
(2)
(3)(三角不等式)对于任意的x,y,z∈X,恒有d(x,y)≤d(x,z)+d(z,y)。
我们看到,如果把范数看做到原点的距离,那么范数空间,在距离空间的基础上,再加一个条件。(这就好像是在水果的基础上,再加一个条件:产于热带,就变成了热带水果)。也就是说,我们可以通过范数来定义距离,但是不能通过距离来定义范数d(x,y) = ||x-y||。
如:(1) 对应直线距离。
(2) 对应折线距离
四、线性赋范空间、线性度量空间
线性赋范空间(和线性度量空间),即是在赋范空间(和度量空间、距离空间)的基础上,再加一个条件:线性结构。
五、内积空间
到上面为止,还不是我们所看到的空间,因为虽然范数代表了向量的长度,但是还没有角度。所以我们需要引入角度的概念,借助内积。
设K是实数域或复数域,H是K上线性空间,如果对H中任何两个向量x,y,都对应着一个数(x,y)∈K,满足条件:
1.(共轭对称性)
2.(对第一变元的线性性)对任何x,y,z∈H及α,β∈K,有(αx+βy,z)=α(x,z)+β(y,z).
3.(正定性)对一切x∈H,有(x,x)≥0且(x,x)=0⇔x=0
到现在为止,内积空间就是我们通俗意义上所认识的空间,也叫作欧几里何空间(有限维的内积空间)。在这个空间上,我们可以提出向量的投影等运算。
六、巴拿赫空间和希尔伯特空间
说到这,我们再说一个概念,交完备性。也即是在取极限的时候,不会跑出去这个空间,就叫做空间的完备性。比如实数集是完备的,而有理数集是不完备的。有理数数列取极限可能是无理数。
赋范空间+完备性=巴拿赫空间
内积空间(无限维)+完备性=希尔伯特空间
换个角度来理解函数空间,如泰勒展开,是将f(x)表示为{}的线性组合的形式;比如傅里叶展开,是将f(x)表示成无限三角函数线性组合的形式。而{}或无限维的三角函数,也叫作一个函数空间的基。
七、拓扑空间
以上都是距离或者线性空间的基础上逐渐增加条件,那如果尝试减少条件呢?比如不要角度的概念,甚至不要距离的概念。比如“连续”的定义:对所有的即为连续。或者写成x0∈D⊂R,f(O(x0,ξ)∩D)⊂O(f(x0),δ)
。。换句话说,拓扑是元素X与其规则τ
合起来。所以,拓扑是弱化了的距离,能描述的范围最广泛。举例,如果距离是水果,范数是热带水果,那么拓扑就是植物。
————————————————
版权声明:本文为CSDN博主「CQ_Liu」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/qq_34099953/article/details/84190508
3 标量空间
- 只有单个的数字等标量
- 包含多个标量
- 标量的加减乘除等也表现为封闭性
- 标量集合中的任何两个标量都可以经过加法和乘法这两种运算得到另一个标量。如果这两种运算满足封闭性、结合律、交换律和对逆元素的要求,那么这些标量就构成了一个标量场。我们熟悉的标量有实数、复数和有理函数等。
4 向量空间/张成空间/线性空间(vector space/ linear space)
- 简而言之:向量空间,就是向量的张成空间
- 就是指定向量的所有线性组合的结果组成的张成空间
4.1 线性空间定义
线性空间指的是,有一个集合由被称为“向量”的“定长坐标序列”凑到一块组成,然后在这个集合中向量之间,定义上两种运算“加法”和“数乘”,二者合起来(所组成的代数结构) 称为线性空间,当然,还有一点额外要求,那就是封闭性:该集合中的任意向量都可以合法地执行这两种运算,结果还在这个集合里。
如果非封闭性,数学家们觉得不如把新算出来的那个玩意也包含到已有的研究对象里来,毕竟本来也是想研究“所有同类”。所以要求这个封闭性。
- 向量组成的一个集合
- 这个集合,以及定义在这个集合上的代数运算,就是线性空间
- 这个线性空间对标了普通的单个数字运算的一般 整数和函数的那个运算空间
4.2 向量空间的表现
- 首先线性空间中有标量和向量两种个对象
- 是最重要的数学空间。向量空间中包含了两种不同的实体---向量和标量。除了两个标量之间的运算外,向量空间中还定义了标量---向量乘法和向量---向量加法。
- 向量空间,从做图上可以看出,无论是2维还是3维的向量空间,都是从原点除法的射线线段,终点坐标可以代表这个向量''
4.3 加法和数乘的封闭性
- 先线性组合概念 --代表了一种计算结果的封闭性,还在这个空间之内
- 线性空间满足两个“运算封闭性”,对所定义的“加法”和“数乘”,假设 α 和 β 是从空间里随便拿出来的两个,则:
- γ=α+β 也在空间里(集合中)
- η=kα 也在空间里(集合中)
4.4 先有“线性组合” 这个概念
- 一组线性无关的向量(基)的所有线性组合,组成的新的向量(坐标),他们全部构成的空间称为向量的张成空间。
- 比如某向量组{v1,v2...vn} 可以是2个,3个或更多
- 但是一般是2个向量组--组成XOY平面,而3个向量组组成XOYOZ空间
- V=span(v1,v2,....,vn) ={k1v1+k2v2+....+kb*vn}
- 也就是某向量组{v1,v2...vn} 进行任意线性组合(加法和标量乘法),其结果仍然在向量空间内,这就是封闭性,所以。
- 前面我专门总结过一篇关于线性相关的
- 线性代数的学习和整理2:什么是线性,线性相关,线性无关 及 什么是线性代数?_奔跑的犀牛先生的博客-CSDN博客矩阵的各种概念矩阵的维数矩阵的基底矩阵的秩。https://blog.csdn.net/xuemanqianshan/article/details/131950205?spm=1001.2014.3001.5501
 https://blog.csdn.net/xuemanqianshan/article/details/131950205?spm=1001.2014.3001.5501
https://blog.csdn.net/xuemanqianshan/article/details/131950205?spm=1001.2014.3001.5501
注意这里,α1是一个数组/向量,而不是数组里的一个具体的数字,比如α1={x1,x2......}
(线性代数矩阵等肯定是研究 数组/向量之间的关系,而绝不是单个数字之间的关系)
如果 A中的多个向量:α1, α2, α3, .....αn ,如果存在不全部为0的一组实数k1,k2,k3....kn,可以使得k1*α1+ k2*α2+...+ kn*αn=0 ,
那么这些向量 α1, α2, α3, α4, .....αn就是线性相关的
4.5 线性组合的意思
- 比如某向量组{v1,v2...vn} 可以是2个,3个或更多
- 但是一般是2个向量组--组成XOY平面,而3个向量组组成XOYOZ空间
- V=span(v1,v2,....,vn) ={k1v1+k2v2+....+kb*vn}
- 也就是某向量组{v1,v2...vn} 进行任意线性组合,其结果仍然在向量空间内。
4.5.1 线性组合的具体方法
线性组合的方法包含如下这些:
- 加法
- 标量乘法
4.6 线性变换
线性变换包含,行的线性变换和列的线性变换
行的线性变换
- 行之间,交换
- 某行乘以倍数
- 某行乘倍数+到其他行
列的线性变换
- 列之间,交换
- 某列乘以倍数
- 某列乘倍数+到其他列
4.7 线性变换(线性映射)的意义?
线性变换,指的是线性空间上,满足
T(α+β)=T(α)+T(β)
T(kα)=kT(α)
那这和直线有什么关系?
- 见线性相关的定义,这个和成正反比例关系很大,和直线的关系也有!
- 标量乘法:数乘运算,可以看作直线上做伸缩+方向变换
- 加法运算:可以用三角形法则,首位相接的形式可以来解释,2个分段向量可以等价于1个总向量图形上生成的还是直线。
- 这种映射把空间里原来的 直线,仍然映射成 直线,而不会“扭曲”成曲线;
- 同时保持原点不动(原点动的就叫“仿射变换”了…)
5 仿射空间(affine space)
5.1 内容
- 而仿射空间与线性空间的区别就在于,它又加了一个对象,这个对象就是“点”。
- 包含:点,标量,向量这3种对象
- 并且它们在运算规则上也不相同。
-
仿射空间它是向量空间的扩展,除了标量和向量外,它还包含了另外一种对象---点。尽管在仿射空间中队两个点以及一个标量没有定义运算,但对一个向量和一个点定义了一种运算---向量-点加法,它的结果是一个点。也可以说有一种称为点---点减法的运算,这种运算由两个点得到一个向量。
或者可以这样理解:仿射空间是假设我们已经定义好了向量空间,然后定义一个点的集合,同时规定了点和向量之间的求和运算(加和的结果仍是搜索点),这个点集就是这个向量空间相伴的仿射空间。
5.2 仿射空间和线性空间的区别
- 线性空间必须满足加法和数乘运算的封闭性,即对于任意向量u,v和标量a,b,u+v和au+bv都必须属于线性空间。
- 仿射空间只需要满足向量之间可以相减,并且可以对向量进行加减运算,不必满足数乘运算的封闭性。
- 线性空间中存在一个零向量,即加上它不改变向量的值。
- 仿射空间中没有零向量的概念。
- 线性空间中的向量有大小和方向的概念,可以进行数量的比较。
- 仿射空间中的向量只有方向的概念,没有大小的概念。
- 线性空间中的向量可以用坐标系表示,向量的坐标具有唯一性,也就是终点终点。
- 仿射空间中的向量不能用坐标系表示,只能用向量之间的关系表示。
- 线性空间中的向量空间是一个线性子空间,即它的子集也满足线性空间的条件。
- 仿射空间中的仿射空间不是一个仿射子空间,它的子集也不必满足仿射空间的条件。
6 欧几里得空间(Euclidean space)
- 仿射空间相当于欧几里得空间去除了距离(保留长度比)和夹角的概念,只保留了直线、直线平行和平行直线上的长度比
- 欧式空间是指坐标空间中(坐标的每一个分量是定义在域上的),规定了坐标的加法和数乘(到这里,称为向量空间),(注意下面这个才是关键!)并定义了坐标之间的内积。定义了内积后,就可以规定空间中不同坐标之间的距离和它们方向的夹角了,具备了欧式几何学所需的几何结构了。
7 向量的各种距离
百度安全验证![]() https://baijiahao.baidu.com/s?id=1652679829019729746&wfr=spider&for=pc百度安全验证
https://baijiahao.baidu.com/s?id=1652679829019729746&wfr=spider&for=pc百度安全验证![]() https://baijiahao.baidu.com/s?id=1747898995916547028&wfr=spider&for=pc
https://baijiahao.baidu.com/s?id=1747898995916547028&wfr=spider&for=pc
7.1 曼哈顿距离

7.2 欧氏距离

7.3 切比雪夫距离


)


)




)




:SQL 动态表 连续查询)




