● 62.不同路径

单解这道题的话，发现第一行或者第一列的这些位置，都只有一条路径走到，所以路径条数都是1。这就是初始化。坐标大于第一行第一列的这些位置，因为机器人只能向下/向右走，所以只能从上个位置向下走和从左边位置向右走，那么应该是上个位置和左边位置路径条数的总和。这就是递推公式。

五部曲：

1、DP数组及其下标的含义：dp[i][j]是起点到坐标(i,j)的路径条数。

2、DP数组如何初始化：dp[0]=1（下图忘记标出来了），第一行或者第一列的都是1。

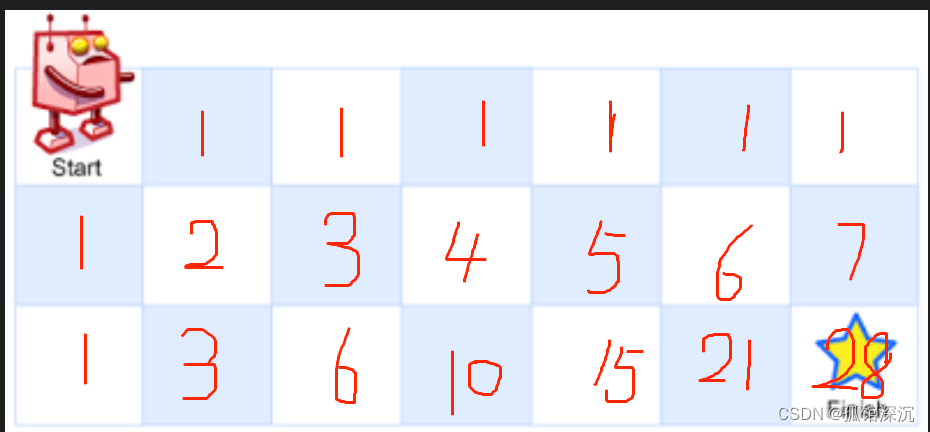
3、递推公式：dp[i][j]=dp[i-1][j]+dp[i][j-1]。(上个位置和左边位置路径条数的总和)

4、遍历顺序：第一行/第一列的初始化后不改动，之后遍历应该从坐标(1,1)开始，所以i是1到m-1，j是1到n-1。这里行优先列优先均可。

5、打印DP数组：

class Solution {
public:int uniquePaths(int m, int n) {vector<vector<int>> dp(m,vector<int>(n,1));//dp数组:m行n列；并且初始化第一行和第一列的为1for(int i=1;i<m;++i)//修改的是（1,1）以及之后的{for(int j=1;j<n;++j){dp[i][j]=dp[i][j-1]+dp[i-1][j];}}return dp[m-1][n-1];}
};

● 63. 不同路径 II

这道题是上道题的扩展，主要区别在于有障碍，那么初始化和递推公式都有变化。

初始化：如果第一列/第一行里面有障碍物，那么第一列/第一行之后的应该初始化为0，因为过去不了，而障碍物之前的还是初始化为1。这里一开始都初始化为0，然后从开始挨个改成1，直到遇到障碍物退出。

递推公式：如果obstacleGrid相应位置没有障碍物，还是使用上一道题的公式；如果有障碍物，也应该更新为0。

代码如下：

class Solution {
public:int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {int m=obstacleGrid.size(),n=obstacleGrid[0].size();vector<vector<int>> dp(m,vector<int>(n,0));//dp数组:m行n列//第一列初始化for(int i=0;i<m;++i){if(obstacleGrid[i][0]==1)break;dp[i][0]=1;}//第一行初始化for(int j=0;j<n;++j){if(obstacleGrid[0][j]==1)break;dp[0][j]=1;}for(int i=1;i<m;++i)//修改的是（1,1）以及之后的{for(int j=1;j<n;++j){if(obstacleGrid[i][j]==1)dp[i][j]=0;else dp[i][j]=dp[i][j-1]+dp[i-1][j];cout<<dp[i][j]<<"  ";}cout<<endl;}return dp[m-1][n-1];}};