无人机集群协同导航构型自适应选择算法

Evandworld
E-mail：evandworld@foxmail.com

摘要

针对卫星定位系统用于无人机集群时成本高、精度低等问题，本文提出一种基于卡尔曼滤波和概率的无人机集群构型自适应选择算法。在自适应扩展卡尔曼滤波的基础上，基于集群的概念判断适用于卫星定位的领航无人机（主机），剩余的从机（僚机）由相对导航确定与主机之间的位置关系，进而进行绝对定位。仿真实验结果表明：所用的无人机集群构型自适应选择算法可以挑选出适合用于卫星定位的无人机，可以为后续的协同导航提供高精度的位置参考点。

关键词

协同导航; 扩展卡尔曼滤波; 无人机集群; 置信传播

引言

基于全球导航卫星系统（Global Navigation Satellite System, GNSS）的导航方法因为使用成本低、导航精度高而被广泛运用，但是在城市、森林等特殊环境下，卫星的信号极易因为特殊的环境或障碍物遮挡，造成不可提前预测的精度降低乃至定位失败的问题。对于无人机（Unmanned Aerial Vehicle, UAV）集群，可将群体中的无人机划分为主机和僚机，并采用协同导航的方法增强群体的总体导航能力。近年来，关于协同导航的研究日益活跃，特别是在支持军事行动和智能交通系统（Intelligent Transportation Systems, ITS）方面，这是因为此类应用经常面临GNSS挑战（拒止）的环境。例如，在军事情况下，车辆可能会从GNSS随时可用的情况转变为完全被拒绝的情况。在 ITS 背景下，城市峡谷通常会导致极端的多径、GNSS 完全阻塞和/或非视距 (LOS) 信号的接收，这可能导致高达数百米的位置误差。
基于上述分析，协同定位技术目前是UAV集群方面的热门问题，主要的研究内容有：基于加权最小二乘法间接融合自身位置、利用卡尔曼滤波（Kalman Filter, KF）融合观测信息和自身增量导航数据、实现精确定位。然而，上述方法均没有考虑到作为参考无人机的主机位置的不确定性，这也是协同定位不同于简单的绝对定位的地方。基于协同导航最终的定位精度不仅取决于测距传感器的能力，还取决于相邻无人机的位置精度和编队这一实事，文献提出了一种适合无人机群体协同导航的协同精度因子计算方法，并设计了一种基于测距信息的协同组合导航方法，有效分析编队对无人机群定位精度的影响。但是这一方法需要进行多次矩阵求逆的运算，计算复杂度随UAVs的数量增长呈现指数级的上升。文献对处于弱GNSS信号区域的UAV，采用相对定位的方法，提高集群整体的定位与导航的性能。
本文提出一种高效且准确的方法，在卡尔曼滤波的基础上，利用概率模型对潜在的领航主机进行误差分析，选择GNSS精度较高的若干个无人机，方便后续僚机的相对定位。

算法解释

将UAV集群中搭载了GNSS/INS/UWB的无人机称为（潜在）主机，其中GNSS和INS可以进行组合导航以获得实时的绝对位置信息，UWB用于与僚机进行相对定位；僚机仅搭配UWB和INS。

自适应EKF预处理

因为KF只适用于线性的系统，而无人机导航信息的滤波具有一定的非线性特征，现有快照LS方法、扩展卡尔曼滤波器（EKF）、联邦卡尔曼滤波器（FKF）、无迹卡尔曼滤波器（UKF）、粒子滤波器（PF）、因子图（FG）等改进方法可以适用于非线性系统。EKF的优点是其相对较低的复杂性以及提供高质量估计的能力，本文研究重点不在融合方法上，因此采用EKF作为潜在主机的组合导航滤波算法。

具体的推导过程此处不再重复叙述。
在GNSS观测误差较大时，观测误差协方差矩阵的R会有变化，因此上述普通的EKF无法继续对系统进行估计。

基于概率模型的主机选择

在获得各个GNSS的位置后，各潜在主机之间的相对位置关系可以通过两种方法进行计算：

1. 基于自适应EKF的组合导航获得的绝对位置作差（下称“GNSS距离”）；
2. 基于UWB直接求解的相对位置数据（下称“UWB距离”）。
   因为UWB的精度较高，在正常环境下可以达到分米级[13]，且其误差与GNSS的误差非同源，因此对比上述两种方法的误差，监测奇异点即可得到每架潜在主机可以作为参考节点的概率，根据实际情况选择概率最高的若干架即可。流程图如图 1：
   

图 1 判断主机的流程图
图中左侧和右侧表示了两个循环，第一个循环（左侧）列出了求解两两UAVs之间的GNSS距离和UWB距离的方法，第二个循环（右侧）给出了根据误差差异求取潜在主机成为主机的概率，并根据设置的数量输出作为主机的UAV序号。其中，阈值a表示正常的GNSS计算出来的误差最大值，对于高斯误差，一般取平均值上浮两倍标准差的值，即： ；阈值b取理想的主机数量，取潜在主机数量的一半即可。需要注意的是，num是一个非负整数，在正常情况下是一个非负整数，所以在确定b的取值时无需精确到小数部分。

仿真与结果

仿真条件设置

共设置10架UAVs，其中5架为装在了GNSS接收机、INS、UWB的潜在主机，5架为仅装在了UWB和INS的僚机。
传感器配置和仿真参数如表：
表 1 传感器配置和仿真参数表
传感器 参数 值 单位
陀螺仪 常值漂移 0.1 deg/s
高斯噪声标准差 0.1 deg/s
一阶马尔可夫漂移误差 0.01 deg/s
一阶马尔可夫时间 3600 s
加速度计 一阶马尔可夫漂移误差 0.01 g
一阶马尔可夫时间 1800 S
GNSS 伪距噪声标准差 1.4 m
伪距多普勒噪声标准差 7 Hz
UWB 高斯噪声标准差 0.1 m
UAVs集群的轨迹如图 2：

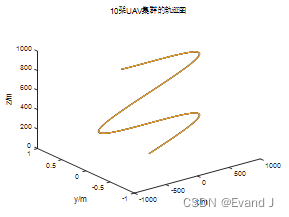
图 2 UAVs集群轨迹图
3.2 结果与分析
基于以上仿真条件，对自适应EKF算法进行精度分析。将非滤波的GNSS定位算法、常规的EKF滤波算法和本文的自适应EKF算法的定位结果进行对比。僚机无协同定位结果是发散的，其误差大小无意义，此处仅列出第1个潜在主机的位置最大误差和均方根误差（RMSE），计算结果如表 2：

表 2 误差统计信息表 单位：m

从表中可以得到如下结论：本文提出的自适应EKF算法不论是误差最大值还是均方根误差，均是最小的，尤其是均方根误差，比非滤波情况降低约91.6%，比常规的EKF滤波算法降低约37.2%。
为了验证算法的主机选择效果，进行100次、2组的蒙特卡洛仿真，统计每次仿真中各个潜在主机被确定为主机的次数，与实际值进行比对。
表 3 主机判定结果统计表

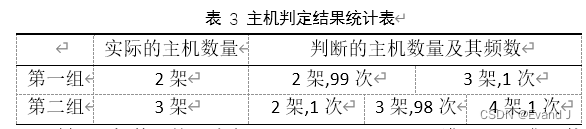
表 3显示，判断主机数量的准确率可以达到98%及以上，满足UAV集群构型的要求，可以为下一步的协同定位提供准确的基准点位置。

结论

本文提出了一种简单的UAV集群构型中自动分类的方法。在自适应EKF的基础上，所提方法可以根据携带的GNSS、INS和UWB判断GNSS数据的置信度，自动选择绝对位置精度较高的UAV作为主机。仿真实验显示，自适应EKF相较于非滤波情况，误差降低约91.6%，相较于常规的EKF滤波算法降低约37.2%，无人机集群构型自适应选择算法的准确度可以达到98%。
后续研究展望：可在本文所述算法筛选的主机和僚机分类的基础上，完成信息交互和协同导航的研究。

程序链接

https://download.csdn.net/download/callmeup/88811767