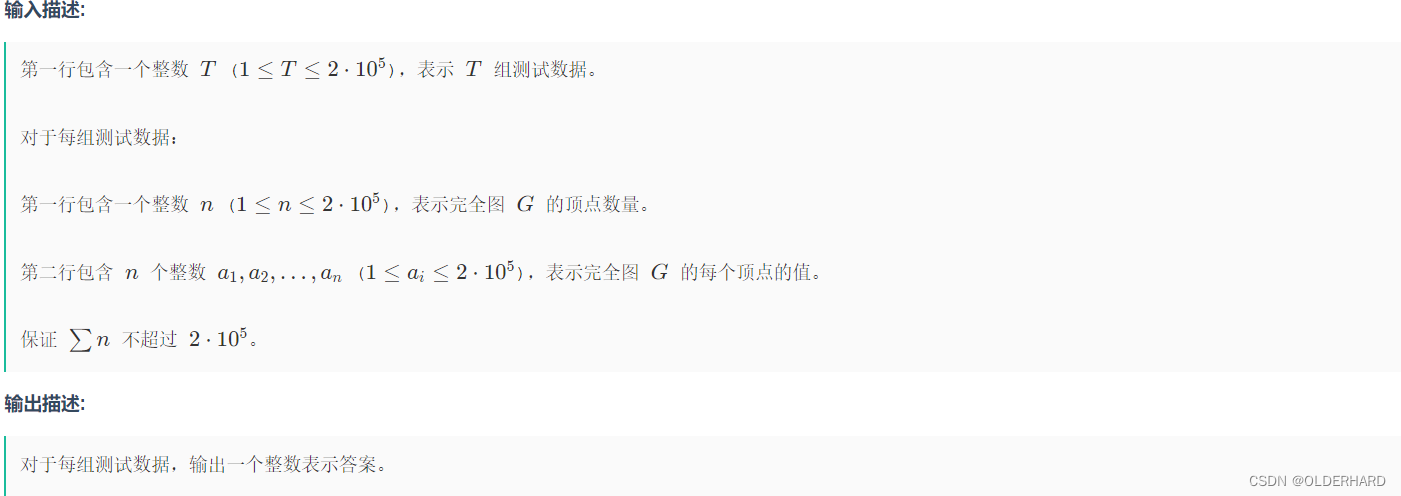
一、Tokitsukaze and Short Path (plus) 

 

解析：
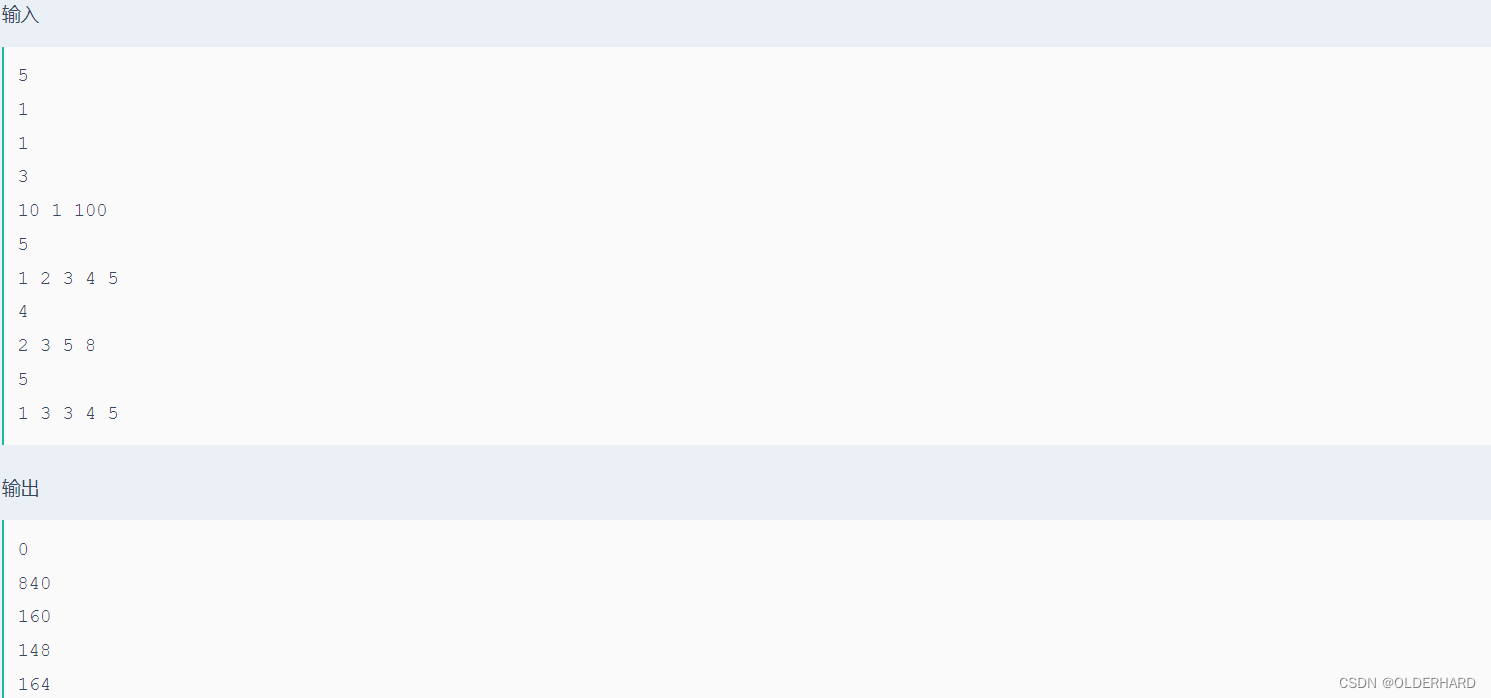
容易知道 对于 u 和 v 两点之间的距离是 2*max(a[u],a[v]),同时这也是这两个点的最短距离，因为如果想要绕路的话，就必须再至少经过一个点，这样的话，就会使得两者的距离变得更大。
所以将数组从小到大排序，计算每个点的贡献即可。

#include <bits/stdc++.h>
#include <math.h>
using namespace std;
#define int long long
#define endl "\n"
#define ios ios::sync_with_stdio(false),cin.tie(nullptr),cout.tie(nullptr);
int gcd(int a,int b) { return b? gcd(b,a%b) : a; }
typedef pair<int,int> PII;
const double PI=acos(-1.0);
const int N=2e6+10;
int n;
int a[N];
void solve()
{cin>>n;for (int i=1;i<=n;i++) cin>>a[i];sort (a+1,a+n+1);int ans=0;for (int i=1;i<=n;i++) ans +=4*(i-1)*a[i];cout<<ans<<endl;
}
signed main()
{ios;int T=1;cin>>T;while (T--) solve(); return 0;
}

二、Tokitsukaze and Short Path (minus)

解析：
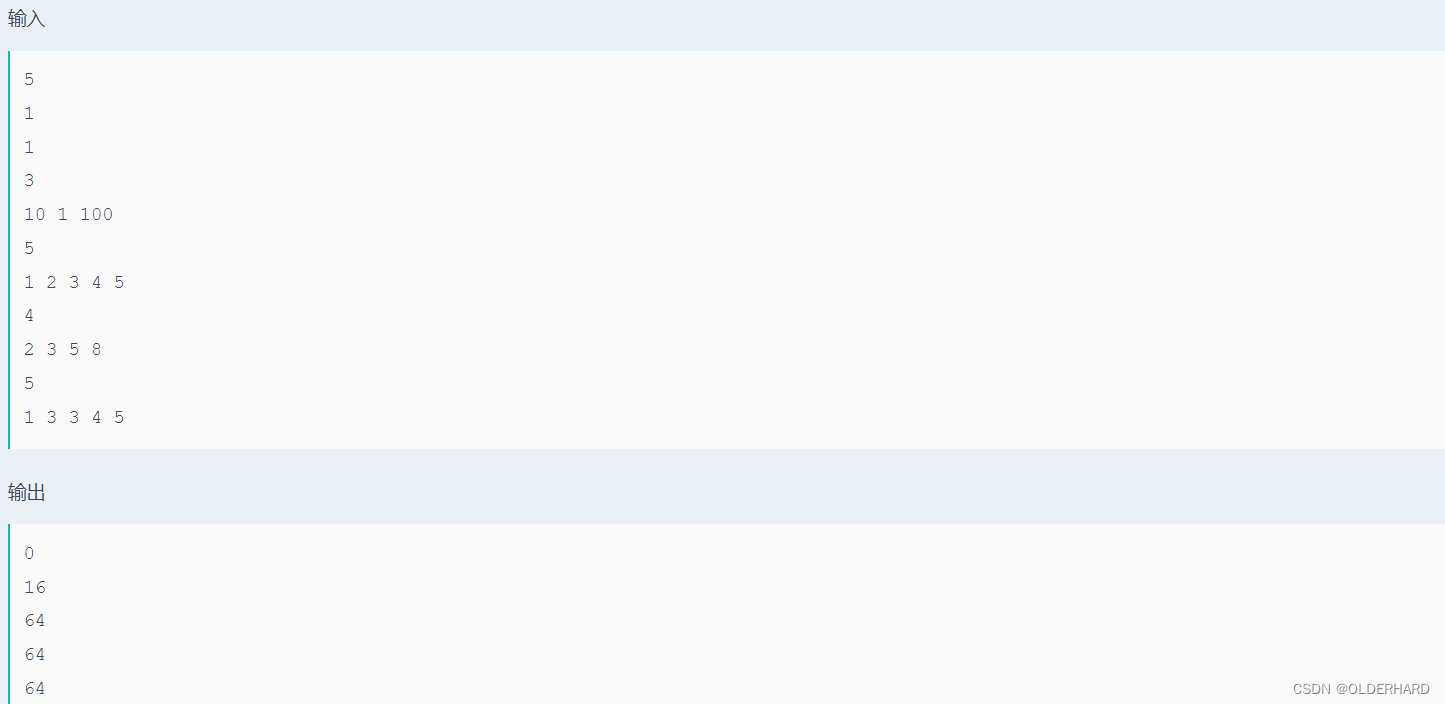
容易知道 对于 u 和 v 两点之间的距离是 2*min(a[u],a[v])。
对于这两个点的最短距离，只有两种情况，不是两者之间的距离，就是 顶点 u 先到达  值最小的点，再从 值最小的点 到达 顶点 v。
所以跟上一个题一样，不过多加了一个判断。
从小到大排序，计算每个点的贡献即可 。

#include <bits/stdc++.h>
#include <math.h>
using namespace std;
#define int long long
#define endl "\n"
#define ios ios::sync_with_stdio(false),cin.tie(nullptr),cout.tie(nullptr);
int gcd(int a,int b) { return b? gcd(b,a%b) : a; }
typedef pair<int,int> PII;
const double PI=acos(-1.0);
const int N=2e6+10;
int n;
int a[N];
void solve()
{cin>>n;for (int i=1;i<=n;i++) cin>>a[i];sort (a+1,a+n+1);int ans=0;for (int i=1;i<=n;i++){int t=a[i];t=min(t,2*a[1]);ans +=4*t*(n-i);}cout<<ans<<endl;
}
signed main()
{ios;int T=1;cin>>T;while (T--) solve(); return 0;
}