1.94. 二叉树的中序遍历
给定一个二叉树的根节点
root,返回 它的 中序 遍历 。示例 1:
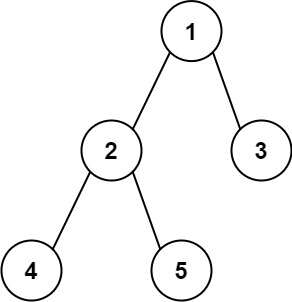
输入:root = [1,null,2,3] 输出:[1,3,2]示例 2:
输入:root = [] 输出:[]示例 3:
输入:root = [1] 输出:[1]提示:
- 树中节点数目在范围
[0, 100]内-100 <= Node.val <= 100
思路:
中序遍历
代码:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:list1=[]def bianli(root):if not root:return bianli(root.left)list1.append(root.val)bianli(root.right)bianli(root)return list12.104. 二叉树的最大深度
给定一个二叉树
root,返回其最大深度。二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。
示例 1:
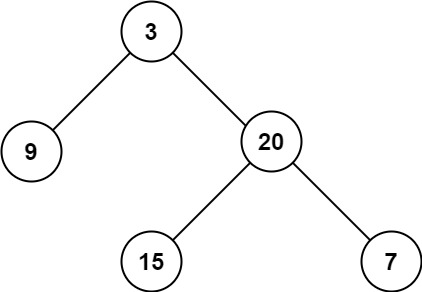
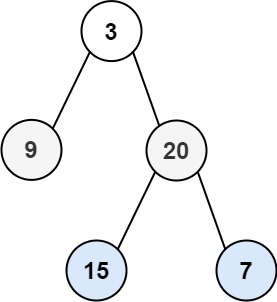
输入:root = [3,9,20,null,null,15,7] 输出:3示例 2:
输入:root = [1,null,2] 输出:2提示:
- 树中节点的数量在
[0, 10^4]区间内。-100 <= Node.val <= 100
思路:
递归中,每次遍历子节点时,深度加一,如果发现为空节点,就将深度还原。每一个树而言,其深度为左右子树深度的最大值。
代码:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:def maxDepth(self, root: Optional[TreeNode]) -> int:# self.maxd=0def bianli(root,depth):if not root:return depth-1left=bianli(root.left,depth+1)right=bianli(root.right,depth+1)return max(left,right)x=bianli(root,1)return x3. 226. 翻转二叉树
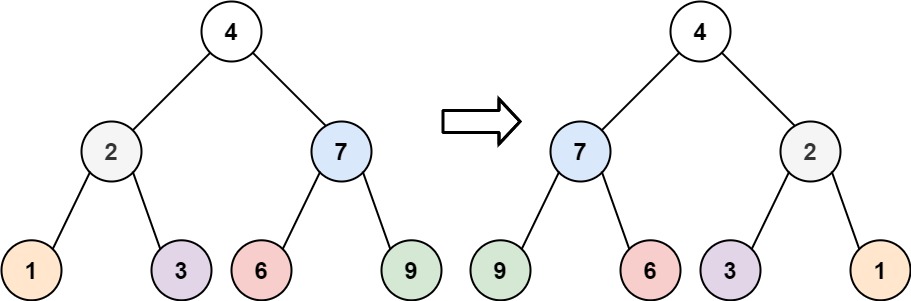
给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。
示例 1:
输入:root = [4,2,7,1,3,6,9] 输出:[4,7,2,9,6,3,1]示例 2:
输入:root = [2,1,3] 输出:[2,3,1]示例 3:
输入:root = [] 输出:[]提示:
- 树中节点数目范围在
[0, 100]内-100 <= Node.val <= 100
思路:
每一个子树都左右交换,递归完成
代码:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:def dfs(p):if p == None:return Noneleft=dfs(p.left)right=dfs(p.right)p.left,p.right=right,leftreturn preturn dfs(root)4.101. 对称二叉树
给你一个二叉树的根节点 root , 检查它是否轴对称。
示例 1:
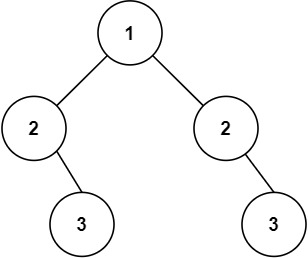
输入:root = [1,2,2,3,4,4,3] 输出:true示例 2:
输入:root = [1,2,2,null,3,null,3] 输出:false提示:
- 树中节点数目在范围
[1, 1000]内-100 <= Node.val <= 100
思路:
后序遍历,外侧和外侧比较,内侧和内侧比较。并且要把子结构中的特殊情况单独列出。
更加详细的解释,请看:代码随想录 (programmercarl.com)
代码:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:def isSymmetric(self, root: Optional[TreeNode]) -> bool:if not root:return Truedef dfs(p,q):if not p and not q:return Trueif not p or not q:return Falseif p.val != q.val:return Falseoutside=dfs(p.left,q.right)inside=dfs(p.right,q.left)if outside and inside:return Trueelse:return Falsereturn dfs(root.left,root.right)5.543. 二叉树的直径
给你一棵二叉树的根节点,返回该树的 直径 。
二叉树的 直径 是指树中任意两个节点之间最长路径的 长度 。这条路径可能经过也可能不经过根节点 root 。
两节点之间路径的 长度 由它们之间边数表示。
示例 1:
输入:root = [1,2,3,4,5] 输出:3 解释:3 ,取路径 [4,2,1,3] 或 [5,2,1,3] 的长度。示例 2:
输入:root = [1,2] 输出:1提示:
- 树中节点数目在范围
[1, 10^4]内-100 <= Node.val <= 100
思路:
使用全局变量保存最大直径。对于一个节点来说,其作为中转点的最大直径=左子树深度+右子树深度
递归体返回当前节点的最大深度,使用遍历来完成!
代码:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:def diameterOfBinaryTree(self, root: Optional[TreeNode]) -> int:self.maxd=0def zuidashedu(root):if not root:return 0left = zuidashedu(root.left)right =zuidashedu(root.right)self.maxd=max(left+right,self.maxd)return max(left,right)+1 x=zuidashedu(root)return self.maxd6.102. 二叉树的层序遍历
给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。
示例 1:
输入:root = [3,9,20,null,null,15,7] 输出:[[3],[9,20],[15,7]]示例 2:
输入:root = [1] 输出:[[1]]示例 3:
输入:root = [] 输出:[]提示:
- 树中节点数目在范围
[0, 2000]内-1000 <= Node.val <= 1000
思路:
使用队列,访问节点,依次将其左右孩子入队,然后按照队列进行访问,访问后出队!
代码:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:if not root:return []queue=[root]#根节点先入队res=[]while queue:res.append([node.val for node in queue])#存储当前层的孩子节点列表ll=[]#遍历当前层的每个节点遍历for node in queue:if node.left:ll.append(node.left)if node.right:ll.append(node.right)#把队列更新成下一层的节点queue=llreturn res


 跳转失效)

)




)








内存加载器(来自ChatGPT))
:基于Doris的有道精品课数据中台建设实践)
)