题目描述：

有一个同学在学习分式。他需要将一个连分数化成最简分数，你能帮助他吗？

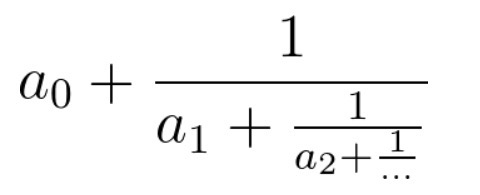
连分数是形如上图的分式。在本题中，所有系数都是大于等于0的整数。

输入的cont代表连分数的系数（cont[0]代表上图的a0，以此类推）。返回一个长度为2的数组[n, m]，使得连分数的值等于n / m，且n, m最大公约数为1。

示例 1：

输入：cont = [3, 2, 0, 2]
输出：[13, 4]
解释：原连分数等价于3 + (1 / (2 + (1 / (0 + 1 / 2))))。注意[26, 8], [-13, -4]都不是正确答案。

示例 2：

输入：cont = [0, 0, 3]
输出：[3, 1]
解释：如果答案是整数，令分母为1即可。

代码：

class Solution {public int[] fraction(int[] cont) {// 分母，count中最后的那个数int n = cont[cont.length - 1];// 分子int m = 1;// i要从倒数第二个开始所以是 i - 2for(int i = cont.length - 2;i >= 0;i --) {// 暂存分母int tmp = n;// 重新计算分分母// 所有加上的那个分数分子都是1，保证了a2*a3+1/a3互为质数就是最简的了，// 所以不用化简n = cont[i] * n + m;// 重新计算分子m = tmp;}// 最后输出结果是{n,m}而不是{m,n}// 因为n = cont[i] * n + m; m = tmp;这两步相当于在调换分子和分母// 当是count[i]是a0项时，是不需要互换的，// 所以输出{n,m}相当于又调换了一次顺序，相当于是调换了两次顺序// 调换两次就是分子分母不变return new int[] {n,m};}
}

 要点提醒：题目中说n,m最大公约数是1，意思是说答案的分子和分母不能够再进行约分。

而每一项count[i]系数加上后面的分数，而后面的分数分子都是1。

就是说系数+分数通分以后=系数*分母+1/分母。

又因为系数*分母+1这一步加了一个1，再除分母的时候就保证了系数*分母+1和分母互为质数。