1. MATLAB进行频域分析举例

以下是一个使用MATLAB进行频域分析的例子。在这个例子中，我们将生成一个含有两个不同频率分量的信号，然后使用快速傅里叶变换（FFT）来分析其频域特性。

main.m文件

clc;close all;clear all;warning off;%清除变量

rand('seed', 500);

randn('seed', 300);

format long g;

%% 本代码由华量信息技术工作室 代码顾问免费提供 联系方式 QQ1579325979

% 创建时间向量

t = 0:0.001:1; % 从0到1秒

% 创建包含两个频率分量的信号

f1 = 5; % 频率1

f2 = 50; % 频率2

y = sin(2*pi*f1*t) + sin(2*pi*f2*t);

% 进行快速傅里叶变换

Y = fft(y);

% 计算频率轴

n = length(t); % 信号长度

f = (0:n-1)*(1/max(t)); % 频率向量

% 画出频域图像

figure;

plot(f,abs(Y));

xlabel('频率 (Hz)');

ylabel('幅度');

title('频域分析');

grid on;

在这个代码中，我们创建了一个信号，其中包含5Hz和50Hz的两个正弦波。然后我们使用fft函数计算信号的频谱，最后我们画出了频谱的图像。

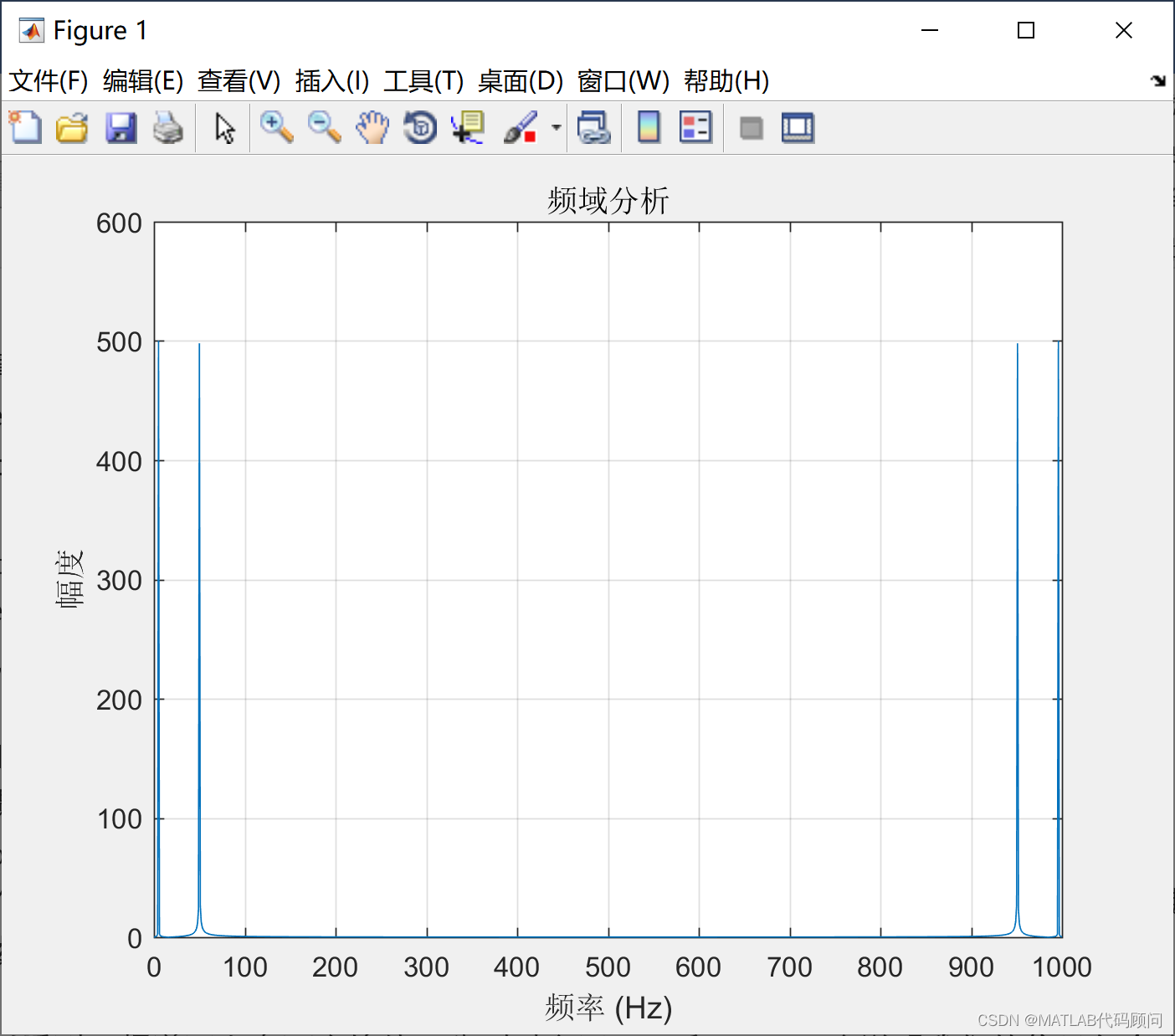
可以看到，频谱图上有两个峰值，分别对应于5Hz和50Hz，这说明我们的信号包含这两个频率的分量。你可以试着改变频率f1和f2的值，看看频谱图如何变化。

2. 频域分析介绍

频域分析是一种分析信号或系统在频率维度下的行为或特性的方法。在频域分析中，我们关注的是信号的频率成分，或者系统对各种频率的输入信号的响应。频域分析提供了一种从不同的角度理解信号和系统的方式。

频域分析的基本工具是傅里叶变换，它可以将一个时域信号转换为一个频域信号。傅里叶变换的基本思想是，任何复杂的信号都可以被看作是许多不同频率的简单正弦波的叠加。傅里叶变换就是找出这些正弦波的频率和幅度。

在系统分析中，频域分析通常涉及到对系统的频率响应的研究。频率响应描述的是系统对各种频率的输入信号的相应大小和相位变化。例如，一个音箱可能对某些频率的音频信号响应更大，这就是它的频率响应特性。

频域分析的主要优点是它可以很清楚地显示出信号的频率成分，或者系统的频率特性。例如，我们可以通过分析一个音频信号的频谱，来了解它包含哪些音调（即频率）。或者，我们可以通过分析一个电路的频率响应，来了解它对哪些频率的信号传输效果最好，对哪些频率的信号有衰减作用。

频域分析和时域分析是两种互补的分析方法，它们从不同的角度揭示了信号和系统的特性。在实际的信号处理和系统分析中，我们通常会根据需要，同时使用这两种分析方法。