A 统计对称整数的数目
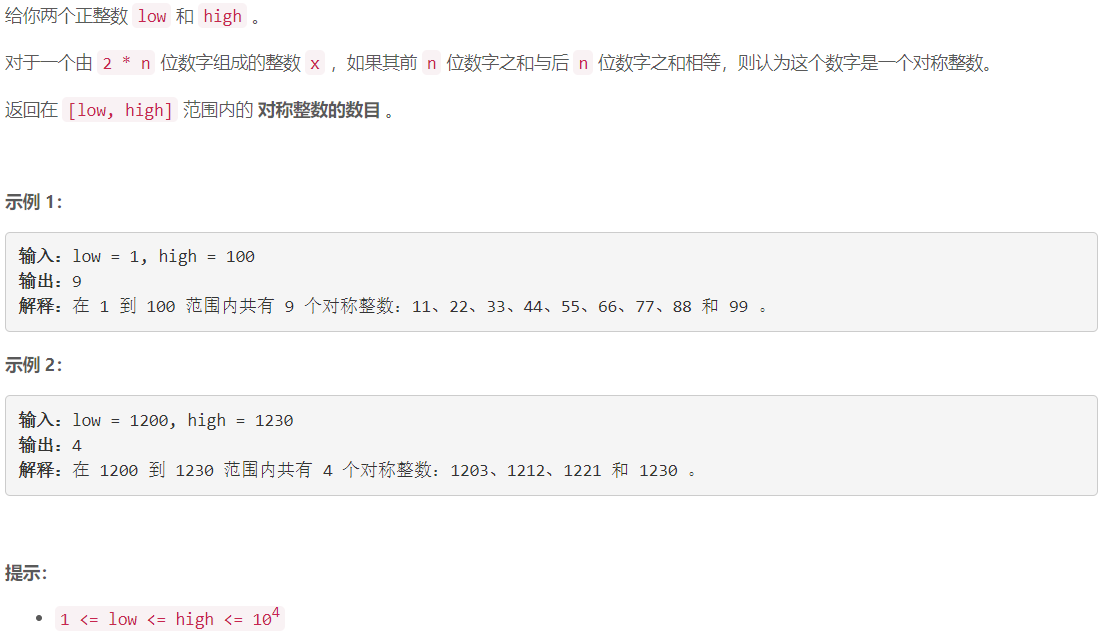
枚举 x x x
class Solution {
public:int countSymmetricIntegers(int low, int high) {int res = 0;for (int i = low; i <= high; i++) {string s = to_string(i);if (s.size() & 1)continue;int s1 = 0, s2 = 0;for (int k = 0; k < s.size(); k++)if (k < s.size() / 2)s1 += s[k] - '0';elses2 += s[k] - '0';if (s1 == s2)res++;}return res;}
};
B 生成特殊数字的最少操作
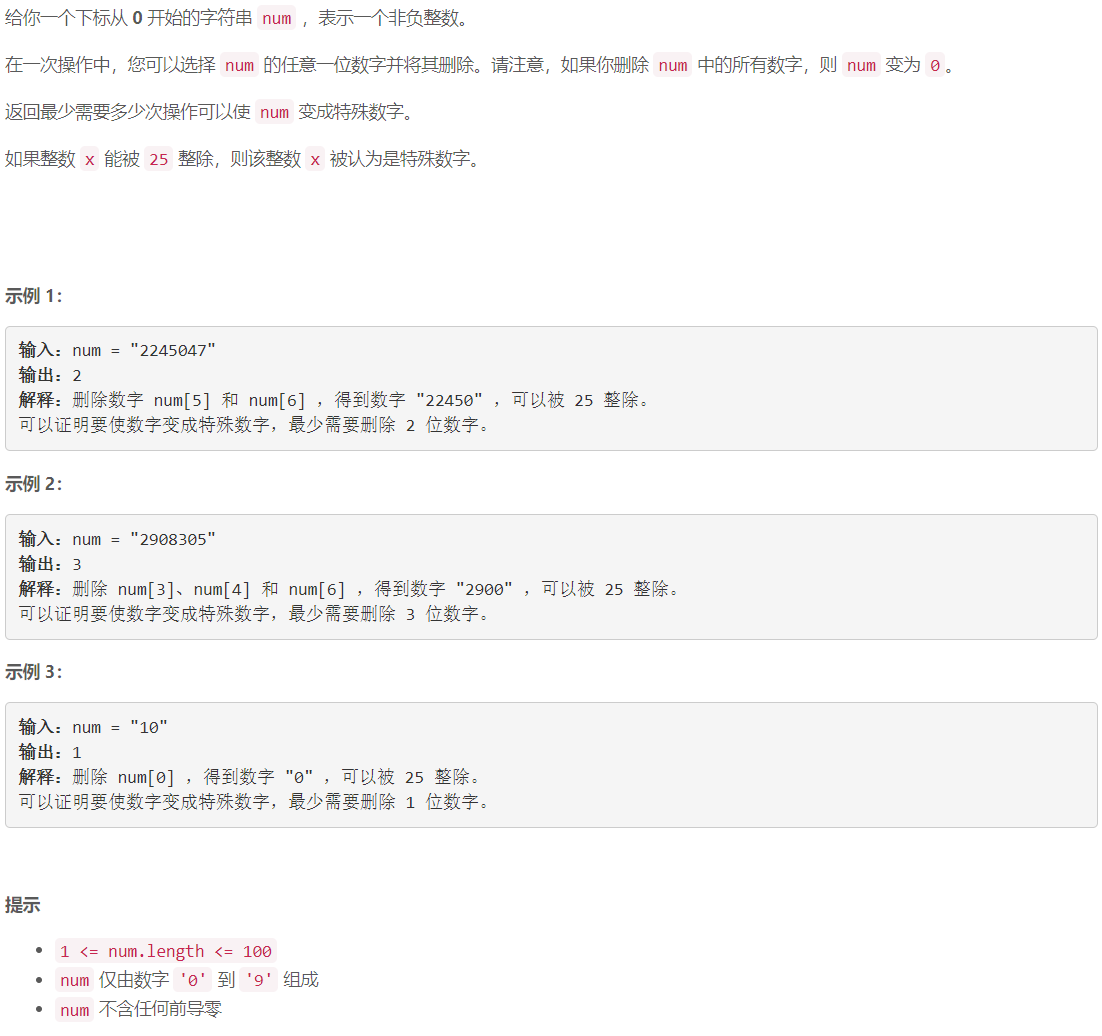
双指针:则若字符串操作完后为 0 0 0 ,设字符串长为 n n n ,则需要 n n n 或 n − 1 n-1 n−1 (字符串中含
0)操作使得字符串变为 0 0 0 , 若字符串操作完后至少有两位数字,则其最后两位只能是 { 25 , 50 , 75 , 00 } \{25, 50, 75, 00\} {25,50,75,00} 其中之一,枚举可能的后两位,用双指针计算要得到当前枚举值的最少操作数
class Solution {
public:int minimumOperations(string num) {vector<string> tar{"25", "50", "75", "00"};int n = num.size();int res = num.find('0') == num.npos ? n : n - 1;for (auto &s: tar) {int i = s.size() - 1;int j = n - 1;int cur = 0;//得到当前枚举值的最少操作数for (; i >= 0 && j >= 0;) {if (s[i] == num[j]) {i--;j--;} else {j--;cur++;}}if (i < 0)res = min(res, cur);}return res;}
};
C 统计趣味子数组的数目


前缀和:设数组 l i li li 有: l i i = { 1 , n u m s [ i ] % m o d = k 0 , n u m s [ i ] % m o d ≠ k li_i=\left\{\begin{matrix} 1 & , nums[i]\%mod=k \\ 0 & , nums[i]\%mod\ne k \end{matrix}\right. lii={10,nums[i]%mod=k,nums[i]%mod=k,设 l i li li 上的前缀和为 p s i = ( ∑ j = 0 j < i l i i ) % m o d ps_i=(\sum_{j=0}^{j<i} li_i)\%mod psi=(∑j=0j<ilii)%mod ,设子数组 n u m s [ l , r ] nums[l,r] nums[l,r] 为趣味子数组,则有: ( p s r + 1 − p s l ) % m o d = k (ps_{r+1}-ps_{l})\%mod=k (psr+1−psl)%mod=k,即有 p s l = ( ( p s r + 1 − k ) % m o d + m o d ) % m o d ps_l=((ps_{r+1}-k)\%mod+mod)\%mod psl=((psr+1−k)%mod+mod)%mod。
class Solution {
public:using ll = long long;long long countInterestingSubarrays(vector<int> &nums, int modulo, int k) {unordered_map<int, ll> cnt;//cnt[val]: 前缀和val出现的次数cnt[0] = 1;//前缀为空int s = 0;//当前前缀和ll res = 0;for (int i = 0; i < nums.size(); i++) {if (nums[i] % modulo == k)s = (s + 1) % modulo;int s_l = ((s - k) % modulo + modulo) % modulo;res += cnt[s_l];cnt[s]++;}return res;}
};
D 边权重均等查询
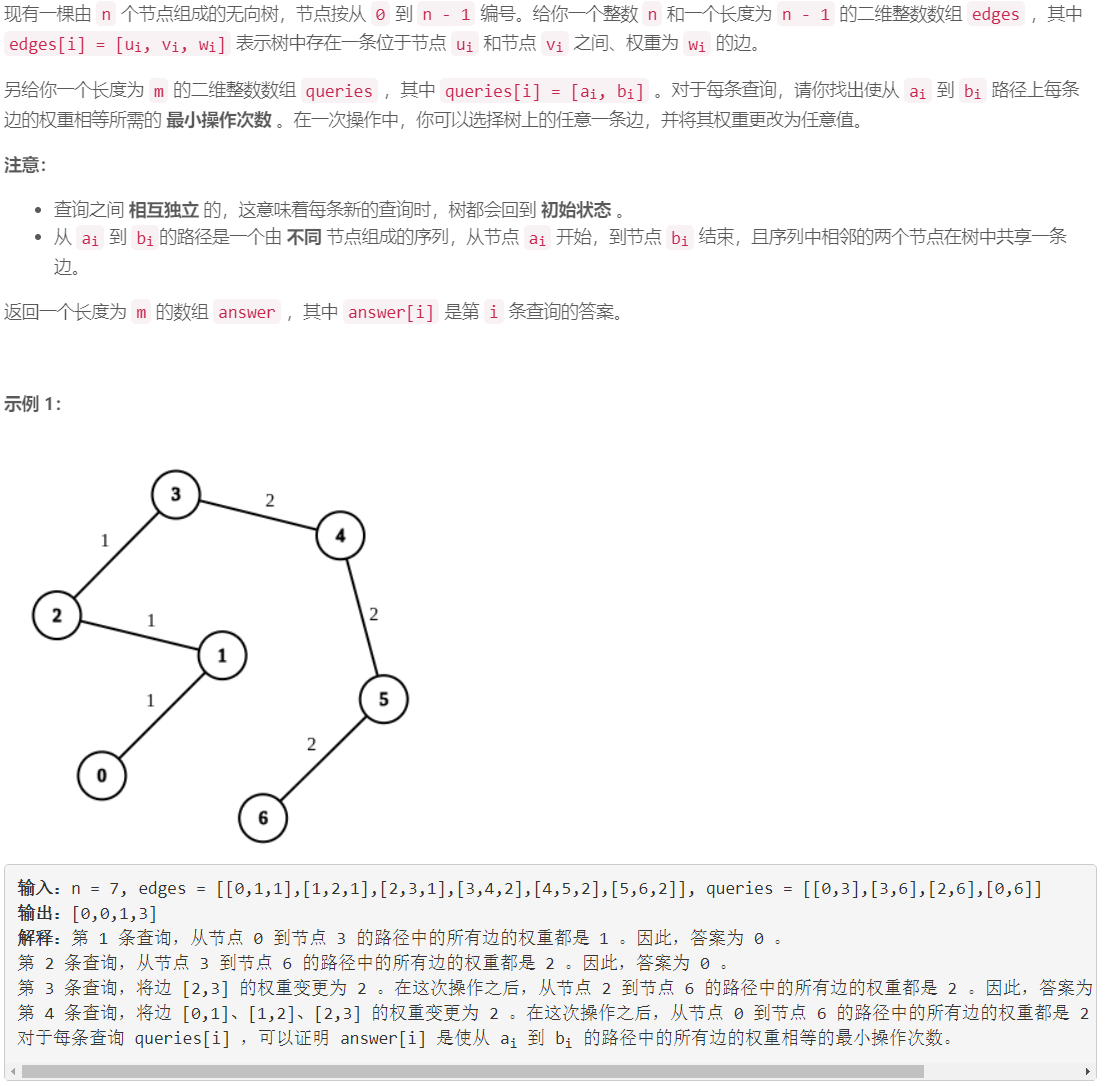
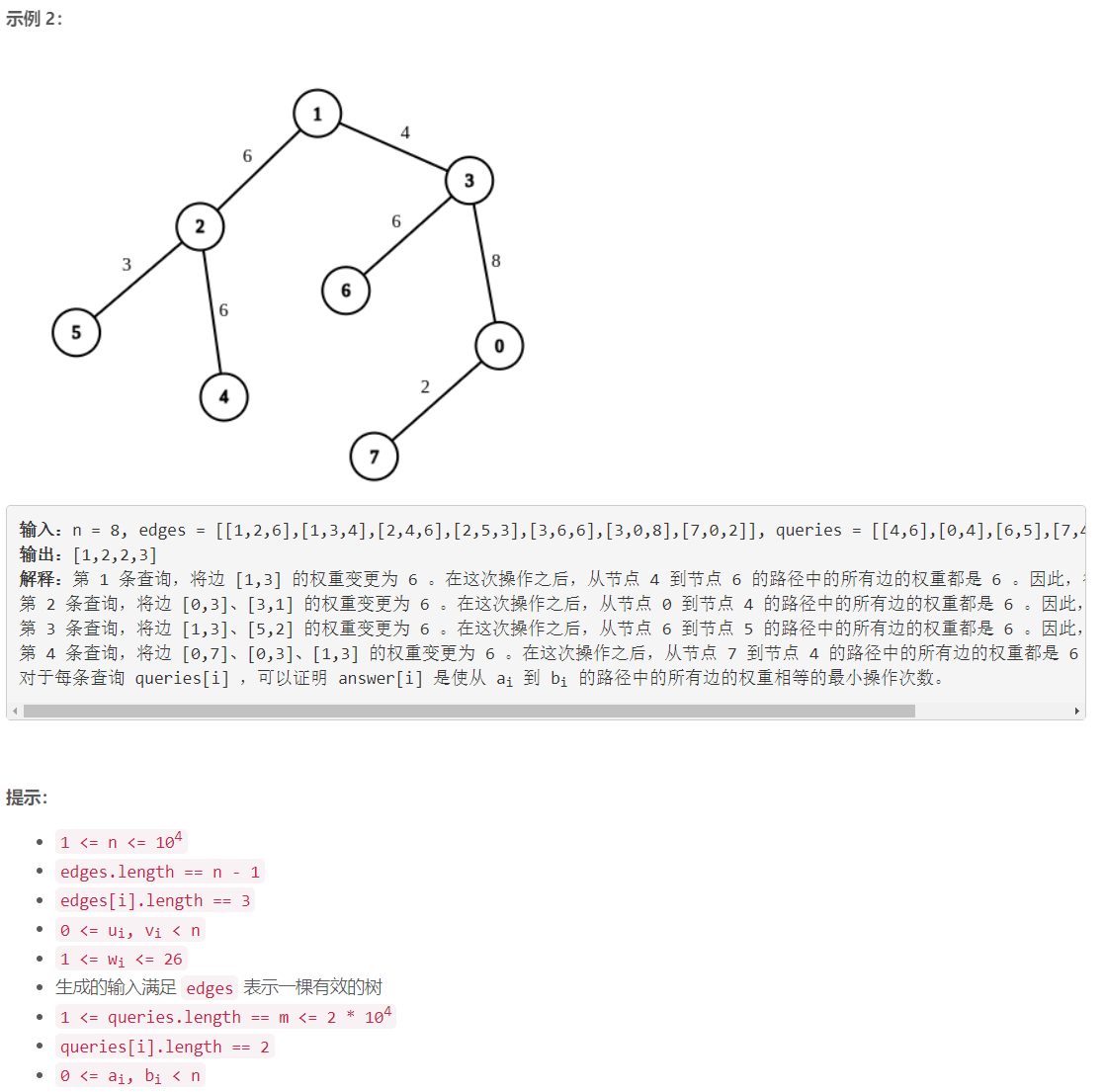
倍增+枚举:1)预处理:设 0 0 0 为树的根节点,枚举边的权重 w _ i d w\_id w_id,从树根开始 d f s dfs dfs ,计算各节点 u u u 到树根的路径上的边数 l e v e l [ u ] level[u] level[u],以及节点 u u u 到树根的路径上边权重为 w _ i d w\_id w_id 的边的数目 s [ u ] [ w _ i d ] s[u][w\_id] s[u][w_id],求倍增数组 p p p: p [ u ] [ j ] p[u][j] p[u][j]为与 u u u 距离为 2 j 2^j 2j的祖先节点。2)对一个查询 ( a , b ) (a,b) (a,b),用倍增的方式求 a a a 和 b b b 的最近公共祖先 c c c ,然后枚举 w _ i d w\_id w_id ,将 a a a 和 b b b 间路径上的边的边权统一为 w _ i d w\_id w_id 的操作数为: ( l e v e l [ a ] − l e v e l [ c ] − ( s [ a ] [ w _ i d ] − s [ c ] [ w _ i d ] ) ) + ( l e v e l [ b ] − l e v e l [ c ] − ( s [ b ] [ w _ i d ] − s [ c ] [ w _ i d ] ) ) \left ( level[a] - level[c] - (s[a][w\_id] - s[c][w\_id]) \right ) + \left ( level[b] - level[c] - (s[b][w\_id] - s[c][w\_id]) \right ) (level[a]−level[c]−(s[a][w_id]−s[c][w_id]))+(level[b]−level[c]−(s[b][w_id]−s[c][w_id]))
class Solution {
public:vector<int> minOperationsQueries(int n, vector<vector<int>> &edges, vector<vector<int>> &queries) {vector<pair<int, int>> e[n];//邻接表int mx_w = 0, mn_w = INT32_MAX;//最大权重、最小权重for (auto &ei: edges) {e[ei[0]].emplace_back(ei[1], ei[2]);e[ei[1]].emplace_back(ei[0], ei[2]);mx_w = max(mx_w, ei[2]);mn_w = min(mn_w, ei[2]);}int level[n], s[n][27];int p[n][15];function<void(int, int, int, int, int)> dfs = [&](int cur, int par, int lev, int sum, int w_id) {if (w_id == mn_w)//倍增数组一轮dfs即可计算for (int i = 0; i < 15; i++)p[cur][i] = i != 0 ? p[p[cur][i - 1]][i - 1] : par;level[cur] = lev;s[cur][w_id] = sum;for (auto &[j, w]: e[cur])if (j != par)dfs(j, cur, lev + 1, w == w_id ? sum + 1 : sum, w_id);};for (int i = mn_w; i <= mx_w; i++)//枚举w_iddfs(0, 0, 0, 0, i);vector<int> res;res.reserve(queries.size());for (auto &qi: queries) {int a = qi[0], b = qi[1];if (a == b) {res.push_back(0);continue;}if (level[a] < level[b])swap(a, b);int c = a;//c最终为a和b的最近公共祖先for (int step = level[a] - level[b], ind = 0; step >= (1 << ind); ind++)if (step >> ind & 1)c = p[c][ind];if (c != b) {int b_ = b;for (int ind = 14; ind >= 0; ind--) {if (p[c][ind] != p[b_][ind]) {c = p[c][ind];b_ = p[b_][ind];}}c = p[c][0];}int res_i = INT32_MAX;for (int w_id = mn_w; w_id <= mx_w; w_id++) {//枚举w_idint t1 = level[a] - level[c] - (s[a][w_id] - s[c][w_id]);int t2 = level[b] - level[c] - (s[b][w_id] - s[c][w_id]);res_i = min(res_i, t1 + t2);}res.push_back(res_i);}return res;}
};









)
)

)




)

