动态规划
记不住过去的人,注定要重蹈覆辙。
定义
对于一个模型为n的问题,将其分解为k个规模较小的子问题(阶段),按顺序求解子问题,前一子问题的解,为后一子问题提供有用的信息。在求解任一子问题时,通过决策求得局部最优解,依次解决各子问题。最后通过简单的判断,得到原问题的解。
经典案例—斐波那契数列
斐波那契数列又称黄金分割数列。因数学家莱昂纳多-斐波那契以兔子繁殖为例引入,故又称兔子数列。
1, 1, 2, 3, 5, 8, 13, 21...
在数学上满足递推的方法定义:
F(0) = 0
F(1) = 1
F(n) = F(n-1) + F(n-2) (n>=2)
def fib(n):if n <= 0:return 0if n == 1:return 1return fib(n-1) + fib(n-2)
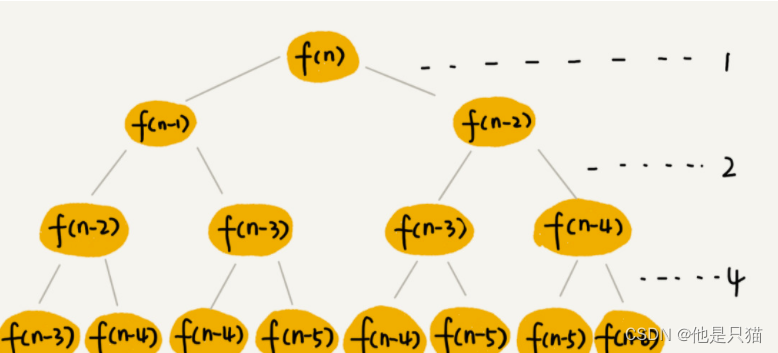
分析:
上图中的二叉树的每个子节点都需要执行一次,如果n= 6,则需要再向下延申,fib(2)就需要执行5次。每次调用时都需要保留上下文,在时间和空间上开销很大。那如果我们把每次计算的结果保存起来,下次用到的时候直接通过查表得方式调用,就可以节省大量得时间,这就是动态规划得基本思想。
动态规划解决
def fib_dp(n):#定义一个dp数组,记录每个n的值,这里n+1长度的便于写代码dp = [-1] * (n+1)#初始化dp[1] = dp[2] = 1for i in range(3, n+1):dp[i] = dp[i-1] + dp[i-2]return dp[n]
解题步骤
核心思想是递推,难点在于dp[i]状态代表什么,然后构造转移矩阵,利用初始条件递推出最终结果。
解题步骤:
- 划分阶段:按照问题的时间和空间特征,把若干问题分为若干个阶段。在划分阶段时,注意划分后的阶段一定要有序或者是可排序的,否则问题就无法求解。
- 确定状态和状态变量:将问题发展到各个阶段时所处于的各种客观情况用不同的状态表示出来。当然,状态的选择要满足无后效性。
- 确定决策并写出状态转移方程:因为决策和状态转移有着天然的联系,状态转移就根据上一阶段的状态和决策来导出本阶段的状态。所以确定了决策,状态转移方程也就可写出。但事实上常常是反过来的,根据相邻两个阶段的状态之间的关系来确定决策方法和状态转移方程。
- 寻找边界条件:给出的状态转移方程是一个递推式,需要一个递推的终止条件或边界条件。
动态规划算法的性质
动态规划的要素:问题的最优解由相关子问题的最优解组合而成,并且可以独立求解子问题(最优子结构)。
- (1)最优化原理:如果问题的最优解包含的子问题也是最优的,就称该问题具有最优子结构,即满足最优化原理;
- (2)无后效性:即某阶段状态(定义的新子问题)一旦确定,就不受这个状态以后决策的影响,也就是说,某状态以后的过程不会影响以前的状态,只与其以前的状态有关。
LeetCode例题
62不同路径
https://leetcode.cn/problems/unique-paths/description/

思路:
每一步只能从向下或向右移动一步,所以对于坐标(i,j)要么从(i-1,j)过来(向下走一步),要么从(i,j-1)过来(向右走一步)。
状态定义:
dp(i, j)表示从左上角走到(i,j)的路径数量
class Solution:def uniquePaths(self, m: int, n: int) -> int:#定义dp数组,用dp(i,j)表示从左上角走到(i,j)的路径数量dp(i,j)dp = [[0] * n for _ in range(m)]# 初始化dp数组,第一行和第一列、应该都是1,都只有一种情况,从左边或者上边过来dp[0][0] = 1for i in range(m):dp[i][0] = 1for j in range(n):dp[0][j] = 1#print(dp) # 可以看下dp [[1, 1, 1, 1, 1, 1, 1], [1, 0, 0, 0, 0, 0, 0], [1, 0, 0, 0, 0, 0, 0]]#计算剩余位置,填充好dp数组for i in range(1, m):for j in range(1, n):dp[i][j] = dp[i-1][j] + dp[i][j-1]print(dp) # [[1, 1, 1, 1, 1, 1, 1], [1, 2, 3, 4, 5, 6, 7], [1, 3, 6, 10, 15, 21, 28]]## 通过查表的方式,返回最终结果return dp[m-1][n-1]LCR 099. 最小路径和
https://leetcode.cn/problems/0i0mDW/description/

思路:
与上一题类似,对于坐标(i,j)要么从(i-1,j)过来(向下走一步),要么从(i,j-1)过来(向右走一步),但是加了条件,每个坐标上的值有了意义,需要进行累加处理。
状态:
设dp为大小m*n的矩阵,其中dp(i,j)的值代表直到走到(i,j)的最小路径和。
转移方程:
- 当可以从左边和上面过来,即左边和上边都不是矩阵边界时:
dp(i, j) = grid(i, j) + min(dp(i-1, j), dp(i, j-1)) - 当只能从上边过来,即左边是矩阵边界时:
dp(i, j) = grid(i, j ) + dp(i, j-1) - 当只能从左边过来,即上边是矩阵边界时(i=0)
dp(i, j) = grid(i, j) + dp(i, j-1) - 在起点时(i=0, j=0)
dp(i, j) = grid(i, j)
class Solution:def minPathSum(self, grid: List[List[int]]) -> int:rows = len(grid)cols = len(grid[0])#其中dp(i, j)的值代表直到走到(i,j)的最小路径和dp = [[0] * cols for _ in range(rows)]for i in range(rows):for j in range(cols):#起点if i == 0 and j == 0:dp[i][j] = grid[i][j]# 中间的点,可以从左边和上边过来elif i != 0 and j != 0:dp[i][j] = grid[i][j] + min(dp[i-1][j], dp[i][j-1])#只能从左边过来elif i == 0 and j != 0:dp[i][j] = grid[i][j] + dp[i][j-1]#只能从上边过来elif i != 0 and j == 0:dp[i][j] = grid[i][j] + dp[i-1][j]#print(dp) # grid =[[1,3,1],[1,5,1],[4,2,1]]return dp[rows-1][cols-1]
1884. 鸡蛋掉落-两枚鸡蛋
https://leetcode.cn/problems/egg-drop-with-2-eggs-and-n-floors/description/

思路:
开始有两枚鸡蛋,所以要分情况讨论,还剩两枚鸡蛋,和一枚鸡蛋;
- 1、如果只有一枚鸡蛋:此时我们需要从1层逐层校验,才能获得确切的值,
- 2、如果有两枚鸡蛋:第一次操作可以在任意一层,如果在k层丢下时碎了一个,那问题就转换成了第一点。
状态:
dp(i, j)表示有 i+1 鸡蛋时,验证 j 层楼需要的最少操作次数,我们可以分开分析 i = 0 和 i = 1的情况:
-
·i = 0 时(只有一枚鸡蛋了):
需要逐层检验,当在 j 层楼时,则dp(0, j) = j -
i = 1时:
-
(1)假设当前在k层的时候第一枚鸡蛋碎了,那么问题就转换成了dp(0, k-1),总共的操作次数是,dp(0, k-1) + 1;
-
(2)如果当前在k层丢下鸡蛋,没有碎,此时可以证明在k层的时候鸡蛋不会碎,那么问题就转化成dp(1, j-k),总共的操作次数是dp(1, j-k) + 1
-
基于(1)(2)取最坏情况:
max(dp(0, k-1), dp(1, j-k) + 1)
-
综上,
dp(1, j) = min(dp(1, j), max(dp(0, k-1), dp(1, j-k) + 1))
-
转移方程:
dp(0, j) = j, i=0
dp(1, j) = min(dp(1, j), max(dp(1, j), max(dp(0, k-1), dp(1, j-k) + 1))), i=1
class Solution:def twoEggDrop(self, n: int) -> int:# dp(i, j)表示有i+1枚鸡蛋时,验证j层楼需要的最少操作次数dp = [[sys.maxsize] * (n + 1) for _ in range(2)]#初始化dp数组dp[0][0] = dp[1][0] = 0 #初始化,只有一枚鸡蛋的情况for j in range(n+1):dp[0][j] = jfor j in range(n+1):#两枚鸡蛋时,在k层是否碎了,分情况讨论for k in range(j + 1):dp[1][j] = min(dp[1][j], max(dp[0][k-1] + 1, dp[1][j-k] + 1))# 查表返回最终结果return dp[1][n]
附录基础
python数据结构与算法理论基础(专栏)
数据结构与算法(python)http://t.csdnimg.cn/Gb6MN
程序 = 数据结构 + 算法;而且在面试过程中这些是必考,必问的内容。内容大纲:基础数据结构(树、链表、栈、队列等)、常见算法(排序算法、递归算法等)。
专栏是基于python的基础知识,是很好的入门学习资料。帮助大家快速理解这些数据结构和常见算法的概念,同时结合力扣题目,也能更好的掌握这些知识,达到在面试中游刃有余的效果。
python基础语法
python基础精讲 http://t.csdnimg.cn/HdKdi
本专栏主要针对python基础语法,帮助学习者快速接触并掌握python大部分最重要的语法特征。
1、基本数据类型和变量
2、分支结构与循环结构
3、函数与异常处理
4、类与模块
5、文件读写
通过本专栏可以快速掌握python的基础语法。



















