蓝桥杯备赛 | 洛谷做题打卡day27
文章目录
- 蓝桥杯备赛 | 洛谷做题打卡day27
- 题目背景
- 题目描述
- 输入格式
- 输出格式
- 样例 #1
- 样例输入 #1
- 样例输出 #1
- 提示
- 题解代码
- 我的一些话
-
[NOIP2003 普及组] 栈
题目背景
栈是计算机中经典的数据结构,简单的说,栈就是限制在一端进行插入删除操作的线性表。
栈有两种最重要的操作,即 pop(从栈顶弹出一个元素)和 push(将一个元素进栈)。
栈的重要性不言自明,任何一门数据结构的课程都会介绍栈。宁宁同学在复习栈的基本概念时,想到了一个书上没有讲过的问题,而他自己无法给出答案,所以需要你的帮忙。
题目描述
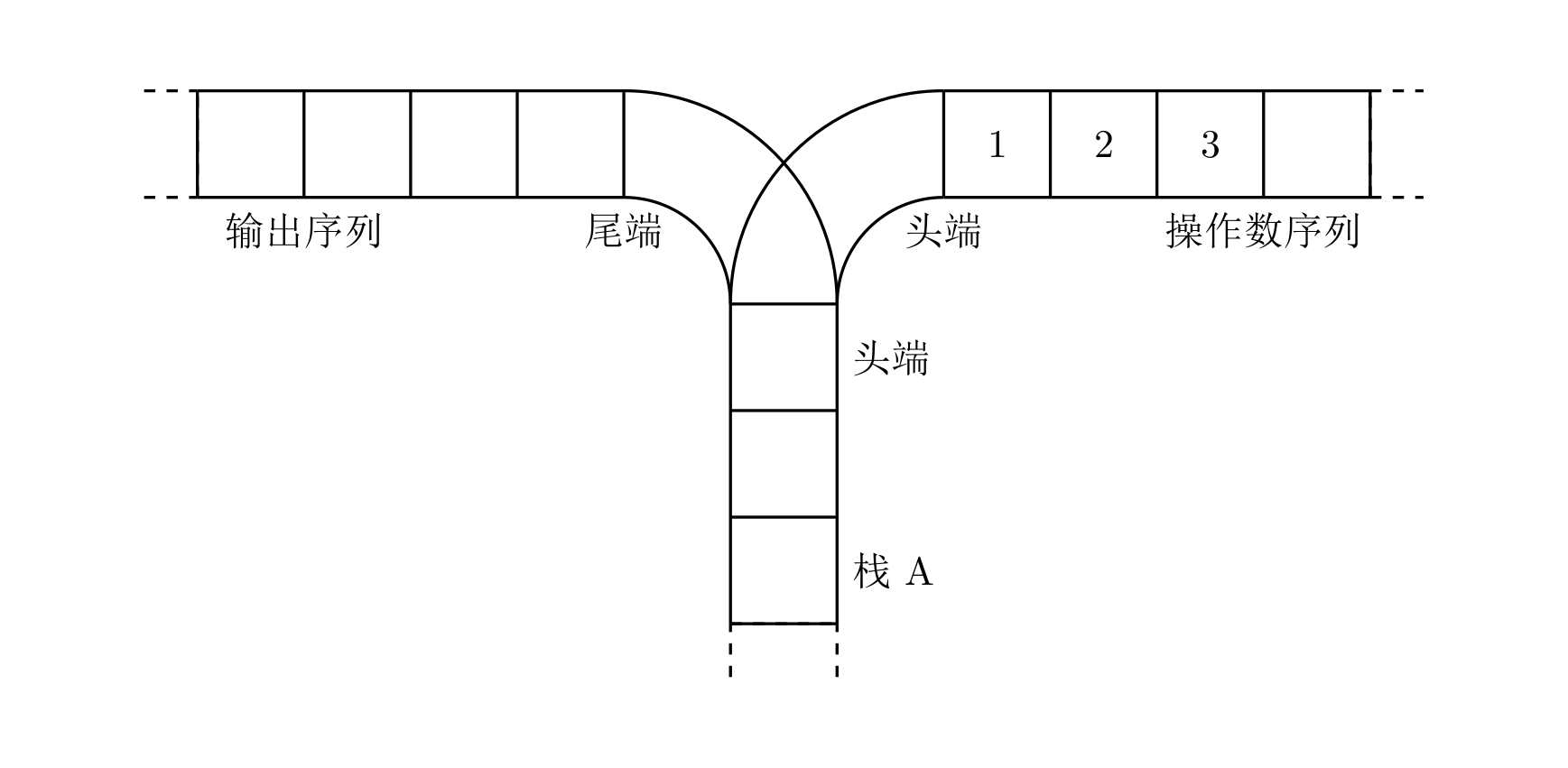
宁宁考虑的是这样一个问题:一个操作数序列, 1 , 2 , … , n 1,2,\ldots ,n 1,2,…,n(图示为 1 到 3 的情况),栈 A 的深度大于 n n n。
现在可以进行两种操作,
- 将一个数,从操作数序列的头端移到栈的头端(对应数据结构栈的 push 操作)
- 将一个数,从栈的头端移到输出序列的尾端(对应数据结构栈的 pop 操作)
使用这两种操作,由一个操作数序列就可以得到一系列的输出序列,下图所示为由
1 2 3生成序列2 3 1的过程。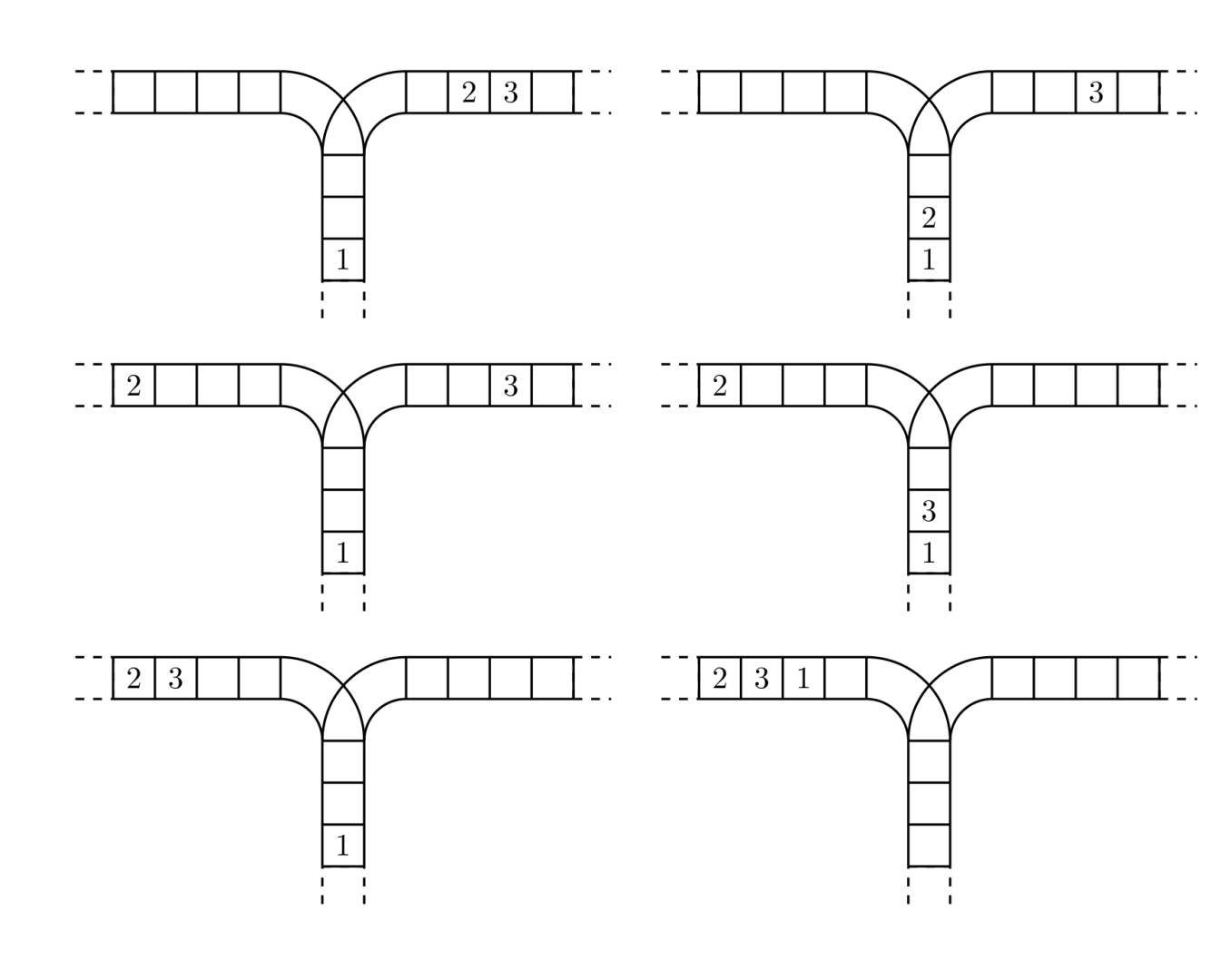
(原始状态如上图所示)
你的程序将对给定的 n n n,计算并输出由操作数序列 1 , 2 , … , n 1,2,\ldots,n 1,2,…,n 经过操作可能得到的输出序列的总数。
输入格式
输入文件只含一个整数 n n n( 1 ≤ n ≤ 18 1 \leq n \leq 18 1≤n≤18)。
输出格式
输出文件只有一行,即可能输出序列的总数目。
样例 #1
样例输入 #1
3样例输出 #1
5提示
【题目来源】
NOIP 2003 普及组第三题
题解代码
学会利用新知,自己多试试并尝试积攒一些固定解答方案,debug,以下是题解代码 ~
#include<iostream>
using namespace std;
long n,f[20][20];//f数组记录方案
long dfs(int x,int y)//x是操作队列里元素的个数,y是栈里的个数
{if(f[x][y]!=0) return f[x][y];//记忆化,走过的方案直接调用if(x==0) return 1;//当操作队列里没有了,就只有一种方案了if(y>0) f[x][y]+=dfs(x,y-1);//栈里不为空的时候才可以把栈里的元素推出f[x][y]+=dfs(x-1,y+1);//操作队列里元素减一,栈里元素加一return f[x][y];//返回方案值
}
int main()
{cin>>n;cout<<dfs(n,0)<<endl;return 0;
}
我的一些话
-
今天学习动态规划,dp属于比较难的部分,这题利用记忆化搜索即可快速解决,需要多动脑,多思考思路还是很好掌握的,虽然一次性AC有一定难度,需要通盘的考虑和理解,以及扎实的数据结构基础才能独立写出AC代码。但无论难易,大家都要持续做题,保持题感喔!一起坚持(o´ω`o)
-
如果有非计算机专业的uu自学的话,关于数据结构的网课推荐看b站上青岛大学王卓老师的课,讲的很细致,有不懂都可以私信我喔
-
总结来说思路很重要,多想想,多在草稿纸上画画,用测试数据多调试,debug后成功编译并运行出正确结果真的会感到很幸福!
-
关于之前蓝桥杯备赛的路线和基本方法、要掌握的知识,之前的博文我都有写,欢迎大家关注我,翻阅自取哦~
-
不管什么都要坚持吧,三天打鱼两天晒网无法形成肌肉记忆和做题思维,该思考的时候一定不要懈怠,今天就说这么多啦,欢迎评论留言,一起成长:)


















遥控小车)
