中小学信息学奥赛CSP-J认证 CCF非专业级别软件能力认证-入门组初赛模拟题一解析（选择题）

CSP-J入门组初赛模拟题一（选择题）

1、以下与电子邮件无关的网络协议是

A、SMTP

B、POP3

C、MIME

D、FTP

答案：D

考点分析：主要考查小朋友们网络相关知识的储备，FTP是文件传输协议和电子邮件无关，所以答案D

2、二进制数1111 0110和0000 1111 进行逻辑异或运算的结果是

A、1111 1001

B、0000 0110

C、1111 1111

D、0000 1001

答案：A

考点分析：主要考查小朋友们二进制相关知识的储备，逻辑异或运算的规则是：同则为0，不同为1，所以答案A

3、布尔型变量占用（）个比特位

A、1

B、2

C、3

D、8

答案：D

考点分析：主要考查小朋友们编程数据类型知识的储备，布尔类型（bool）占用一个字节，一个字节等于8位，所以答案D

4、以下程序段执行完毕后,i和s 的值分别是

int i,s = 0;
for(i = 1;i <= 5;i = i + 2)s = s + i;

A、5和9

B、7和9

C、5和7

D、9和7

答案：B

考点分析：主要考查小朋友们C++知识的储备，i的取值为：1，3，5，7；7不满足条件所以退出循环，s的值为：1+3+5=9，所以答案C

5、已知有序表(13,18,24,35,47,50,62,83,90,115,134),当折半查找值为 90 的元素时,查找成功的比较次数为

A、5

B、2

C、3

D、4

答案：B

考点分析：主要考查小朋友们编程相关知识，题目考查的是折半查找，折半查找是从中间开始找，如果数字大于中间数，就从右半部分中间查找；如果小于就从左半部分中间查找，如此反复每次都是从剩下数字的中间查找。列表中右11个数，所以第一次从第6个数字50开始查找，发现90大于50，所以第二次从右半部分也就是62到134这5个数字查找，查找的数字就是第3个也就是90，找到了，所以列表查找的次数为2；答案B

6、数组不具有的特点是

A、插人、删除不需要移动元素

B、可随机访问任一元素

C、是一块连续的内存空间

D、所需空间与线性长度成正比

答案：A

考点分析：主要考查小朋友们C++数组相关知识，数组插入和删除都需要移动元素，答案A

7、用冒泡排序的方法对一个长度为 n 的数据进行排序,平均时间复杂度为

A、

B、 $O(n\log_{2} n)$

C、 $O(n)$

D、 $O(n\sqrt{n})$

答案：A

考点分析：主要考查小朋友们冒泡排序相关知识，冒泡排序是一种基本的排序算法，其原理是通过比较相邻元素的大小，将较大的元素往后交换，从而实现元素的逐渐有序；

每一次遍历过程中，需要比较的次数为n-1次。所以，总的比较次数为 (n-1)+(n-2)+(n-3)+...+3+2+1 = n(n-1)/2。每一次遍历过程中，最多需要交换的次数为n-1次。所以，总的交换次数也为n(n-1)/2。因此，冒泡排序的时间复杂度可以表示为 $O(n^{2})$

8、由4个节点构成的形态不同的二叉树有（）种

A、16

B、14

C、20

D、10

答案：B

考点分析：主要考查小朋友们二叉树相关知识，所谓的二叉树指的是一种树形结构，每个元素称为一个节点，一个节点可以有两个子节点，所以得名二叉树；4个节点组成的二叉树分两种情况，一种是每个节点都只有一个节点情况，这种情况有8种结构（根节点1个，其余3个节点都可以有左右节点两种选择，所以共有2*2*2=8种），这种情况度为4。还有一种情况是度为3：根节点有左右两个节点，剩下一个节点可以是根节点左右两个节点的任意左右子节点，就有4种情况；接着还可以是根节点只有一个子节点，另外三个节点为一个完全二叉树；由于根节点有左右两个节点，所以有两种情况，一共就是：8+4+2=14，答案B

9、以下 4 个数中最大的素数是

A、91

B、89

C、119

D、93

答案：B

考点分析：主要考查小朋友们素数相关知识，素数也叫质数，除了1和本身外没有因素；91=13*7，119=17*7，93=31*3；所以答案B

10、45 和 30 的最小公倍数是

A、30

B、45

C、90

D、180

答案：C

考点分析：主要考查小朋友们最小公倍数相关知识，最小公倍数等于两数相乘除以最大公约数=45*30/15=90，答案C

11、深度为k的二叉树上,最多含有( )个节点

A、2k-1

B、2k

C、 $2^{k}-1$

D、 $2^{k-1}$

答案：C

考点分析：主要考查小朋友们二叉树相关知识，题目要求是最多有多少个，最多的情况就是为一个满二叉树，也就是所有的非叶子节点都有两个子节点；而深度为K的，第K层的叶子就有 $2^{k-1}$ 个，所有节点个数就是：1+2+3+... $2^{k-1}$ = $2^{k}-1$ ；答案C

12、字符串“abcab”本质不同的子串个数为

A、12

B、13

C、14

D、15

答案：A

考点分析：主要考查小朋友们子串相关知识，不同的子串为：a,b,c,ab,bc,ca,abc,bca,cab,abca,bcab,abcab共12个，答案A

13、十进制小数 11.375 对应的二进制数是

A、1011.011

B、1011.01

C、1101.101

D、1101.011

答案：A

考点分析：主要考查小朋友们进制转换相关知识，将一个十进制整数转换为二进制数的方法是通过除以2的余数来逐步获取，将得到的余数按照从下到上的顺序组成二进制数；十进制小数转二进制：将十进制小数部分乘以2，将结果的整数部分取出，作为二进制的第一位。将结果的小数部分保留，继续进行下一步计算；算到没有小数为止得到的就是二进制数值。所以答案A

14、一棵6节点二叉树的中序遍历为 ABDGECF,先序遍历为 DBACEGF,后序遍历为

A、DGBEFAC

B、ABGEFCD

C、GBEACFD

D、ABCDEFG

答案：A

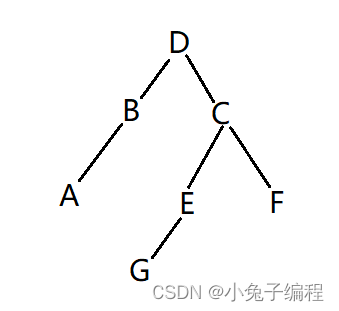
考点分析：主要考查小朋友们二叉树的遍历规则，二叉树遍历分为三种：先序遍历：根→左子树→右子树；中序遍历：左子树→根→右子树；后序遍历：左子树→右子树→根；所以从线序遍历可以得知D为根节点，因此后序遍历必须是D结尾，排除AD选项，而从中序遍历可以得知G为根的右子树，因此后序遍历不可能是G开头；所以答案B；根据中序遍历和线序遍历得到二叉树如下图：